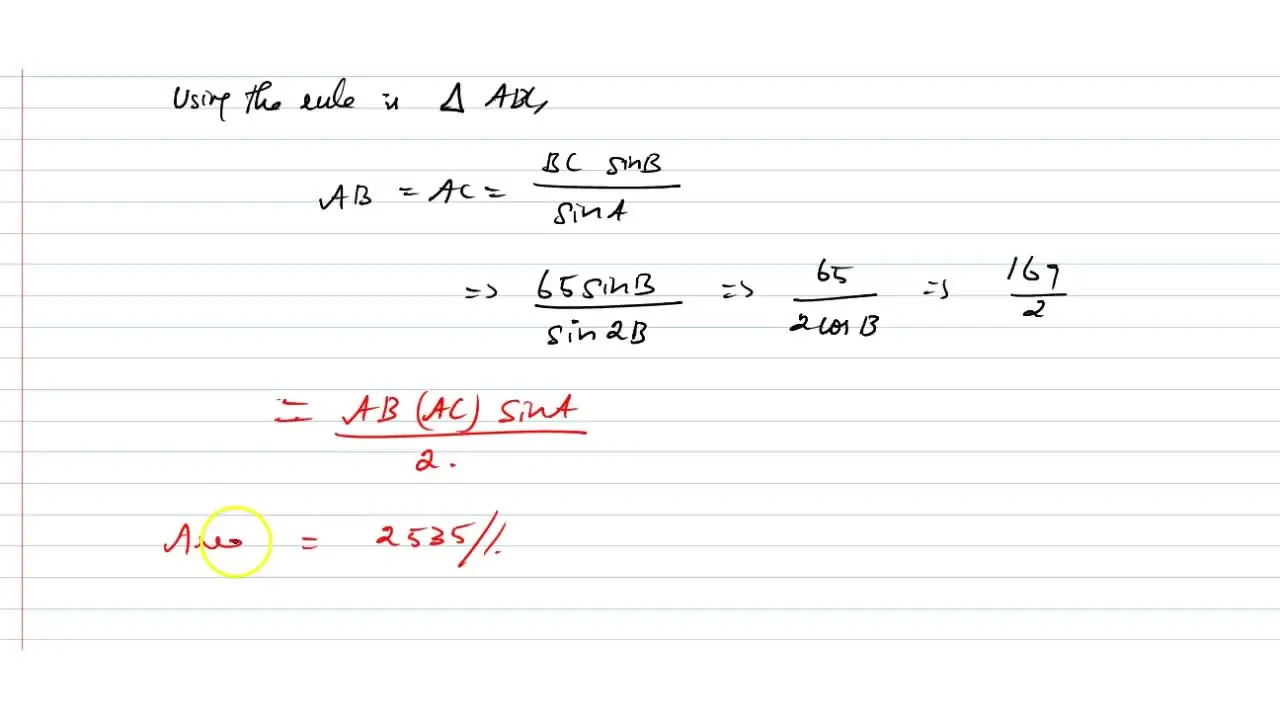Triangle ABC is isosceles with AB=ACandBC=65cm. P is a point on BC such that the perpendiculardistances from P to ABandAC are 24cmand36cm, respectively. The area of triangle ABC (in sq cm is)
1254
1950
2535
5070
The correct Answer is:C

Δ=12b2sin2θ=b2sinθcosθ...(i)
Now, x24=65−x36 (∵ΔPMB=≅ΔPNC)
or 60x=(24)(65) or x=26
∴sinθ=1213andcosθ=513
Now, bsinθ=65sin2θ
or b=652cosθ=(65)(13)(2)(5)=1322
From Eq. (i) we get
Δ=1344×1213×513=(169)(15)=2535
Related Playlists
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Multiple correct answer type24videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Linked comprehension type34videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Concept application exercise 5.114videos
PROPERTIES AND SOLUTIONS OF TRIANGLE
- BOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )1videos
PROGRESSION AND SERIES
- BOOK - CENGAGE ENGLISHCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Archives(Matrix Match Type)1videos
RELATIONS AND FUNCTIONS
Similar Questions
ABC is an isosceles triangle with AB = AC =13 cm and BC = 10 cm. Calculate the length of the perpendicular from A to BC.
View SolutionABC is a triangle in which AB=ACandD is a point on AC such that BC2=AC×CD.Prove that BD=BC.
View SolutionABC is an isosceles triangle with AB = AC = 2a and BC = a . If AD⊥BC, find the length of AD .
View SolutionABC is a triangle in which AB = AC = 4 cm and ∠A=90∘. Calculate:
the length of perpendicular from A to BC.View SolutionAngle BAC of triangle ABC is obtuse and AB = AC. P is a point in BC such that PC = 12 cm. PQ and PR are perpendiculars to sides AB and AC respectively. If PQ = 15 cm and PR = 9 cm, find the length of PB.
View SolutionConstruct a triangle ABC in which AB = 6cm, BC= 7 cm and CA = 6.5 cm. Find a point P equidistant from B and C, and also equidistant from AB and BC.
View SolutionIn triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find :
cos BView SolutionIn triangle ABC, AB = AC = 15 cm and BC = 18 cm. Find :
sin CView Solution△ABC is an isoscles triangle with AB= AC= 13 cm and the length of altitude from A on BC is 5 cm, find BC.
View SolutionConstruct a triangle ABC, with AB =6 cm, AC = BC = 9 cm.Find a point 4cm from A and equidistant from B and C.
View Solution