The perimeter of an isosceles triangle is 32 cm. The ratio of the equal side to its base is 3:2. Find the area of the triangle.
31√2cm2
32√2cm2
30√2cm2
42√2cm2
The correct Answer is:B
Let ABC be an isoceles triangle with perimeter 32cm. We have, ratio of equal side to its base is 13:2.
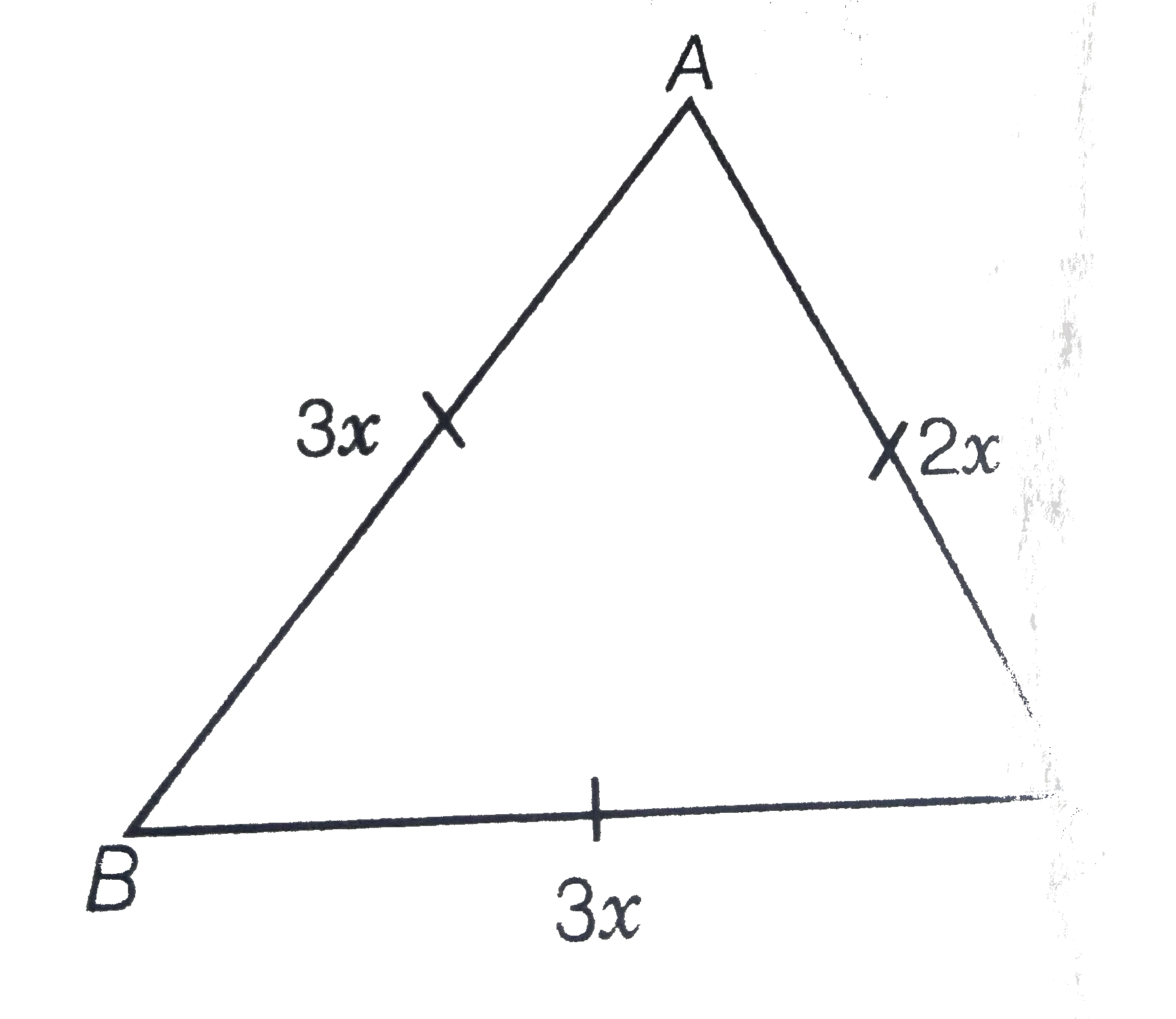
Let sides of triangle be AB=AC=3x,BC=2x
∵Perimeter of a triangle=32m
Now, 3x+3x+2x=32
⇒ 8x+32
⇒ x+4
∴ AB=AC=3×4=12cm
and BC=2x=2×4=8cm
The sides of a triangle are a =12 cm, b=12 cm
and C=8cm.
∴Semi-perimeter of an isosceles triangle,
s=a+b+c2
=12+12+82=322=16cm
∴Area of an isosceles△ABC=√s(s−a)(s−b)(s−c) [by Heron's formula]
=√16(16−12)(16−12)(16−8)=√16×4×4×8
⇒ =4×4×2√2cm2=32√2cm2
Hence, the area of an isosceles triangle is 32√2cm2.
Topper's Solved these Questions
Similar Questions
The perimeter of an isosceles triangle is 40 cm. The base is two-third of the sum of equal sides. Find the area of the triangle .
View SolutionThe perimeter of an isosceles triangle is 30 cm and each of the equal sides measures 12 cm. Find the area of the triangle by using Heron's formula.
View Solution
Knowledge Check
- Question 1 - Select One
The perimeter of an isosceles triangle is equal to 14 cm and the lateral side is to the base in the ratio 5 : 4. The area of the triangle is (a) 21 cm2 (b) 0.5√21cm2 (c) 1.5√21cm2 (d) 2√21cm2
A12√21cm2B32√21cm2C√21cm2D2√21cm2 - Question 2 - Select One
The base of an isosceles triangle is 16 cm. If both the equal sides be 17 cm each, find the area of the triangle.
A90 cm2B100 cm2C120 cm2D110 cm2 - Question 3 - Select One
The perimeter of an isosceles right angled triangle is 2p cm. Its area is -
A(2+√2)p2sqcmB(3+2√2)psqcmC(3−2√2)p2sqcmD(2−√2)psqcm
The perimeter of an isosceles triangle is 32 cm while its equal side stogether measure 18 cm. Find the third side and each of the equal sides.
View SolutionThe base of an isosceles triangle is 48 cm and one of its equal sides is 30 cm. Find the area of the triangle
View SolutionAn isosceles triangle has perimeter 30cm and each of the equal sides os 12 cm. Find the area of the triangle.
View SolutionThe perimeter of an isosceles triangle is equal to 14 cm and the lateral side is to the base in the ratio 5 : 4. The area of the triangle is (a) 21 cm2 (b) 0.5√21cm2 (c) 1.5√21cm2 (d) 2√21cm2
View SolutionThe perimeter of an isoceles triangle is 544 cm and its equal sides is 5/6 times of its base then the area of triangle (in cm2) is-
View Solution
