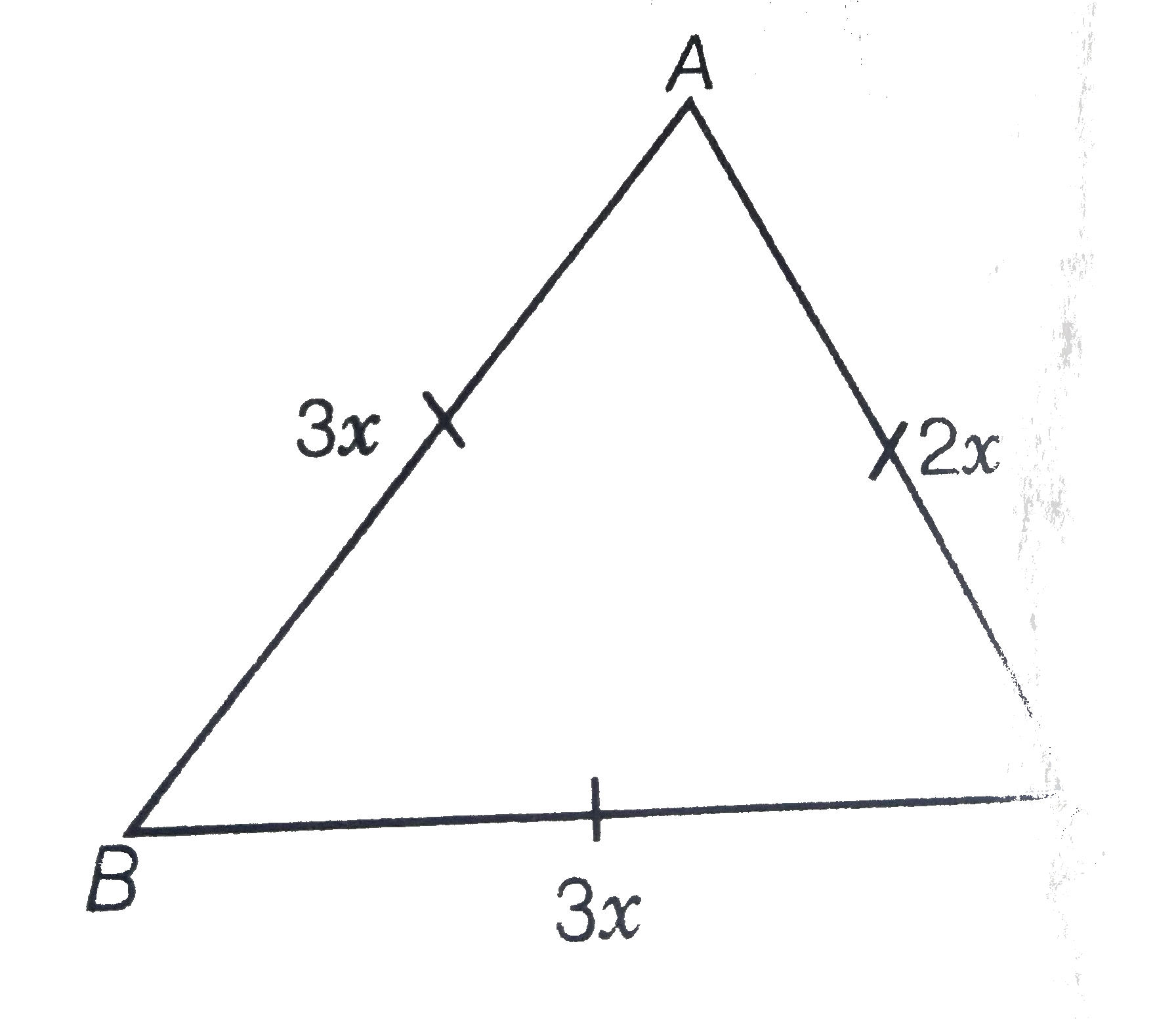
The perimeter of an isosceles triangle is $32$ cm. The ratio of the equal side to its base is $3 : 2$ . Find the area of the triangle.

A

$31 \sqrt{2} c m^{2}$

B

$32 \sqrt{2} c m^{2}$

C

$30 \sqrt{2} c m^{2}$

D

$42 \sqrt{2} c m^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Let $A B C$ be an isoceles triangle with perimeter $32 c m .$ We have, ratio of equal side to its base is $13 : 2 .$
$Let sides of triangle be A B = A C = 3 x, B C = 2 x$
$∵ Perimeter of a triangle = 32 m$
$Now, 3 x + 3 x + 2 x = 32$
$\Rightarrow 8 x + 32$
$\Rightarrow x + 4$
$∴ A B = A C = 3 \times 4 = 12 c m$
$and B C = 2 x = 2 \times 4 = 8 c m$
The sides of a triangle are a =12 cm, b=12 cm
$and C = 8 c m$ .
$∴$ Semi-perimeter of an isosceles triangle,
$s = \frac{a + b + c}{2}$
$= \frac{12 + 12 + 8}{2} = \frac{32}{2} = 16 c m$
$∴ Area of an isosceles △ A B C = \sqrt{s (s - a) (s - b) (s - c)} [by Heron's formula]$
$= \sqrt{16 (16 - 12) (16 - 12) (16 - 8)} = \sqrt{16 \times 4 \times 4 \times 8}$
$\Rightarrow = 4 \times 4 \times 2 \sqrt{2} c m^{2} = 32 \sqrt{2} c m^{2}$
Hence, the area of an isosceles triangle is $32 \sqrt{2} c m^{2}$ .

|

Updated on:21/07/2023

Class 9 MATHS HERONS FORMULA

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The perimeter of an isosceles triangle is equal to 14 cm and the lateral side is to the base in the ratio 5 : 4. The area of the triangle is (a) 21 cm2 (b) $0.5 \sqrt{21} c m^{2}$ (c) $1.5 \sqrt{21} c m^{2}$ (d) $2 \sqrt{21} c m^{2}$
A $\frac{1}{2} \sqrt{21} c m^{2}$
B $\frac{3}{2} \sqrt{21} c m^{2}$
C $\sqrt{21} c m^{2}$
D $2 \sqrt{21} c m^{2}$
Question 2 - Select One
The base of an isosceles triangle is 16 cm. If both the equal sides be 17 cm each, find the area of the triangle.
A90 $c m^{2}$
B100 $c m^{2}$
C120 $c m^{2}$
D110 $c m^{2}$
Question 3 - Select One
The perimeter of an isosceles right angled triangle is 2p cm. Its area is -
A $(2 + \sqrt{2}) p^{2} s q c m$
B $(3 + 2 \sqrt{2}) p s q c m$
C $(3 - 2 \sqrt{2}) p^{2} s q c m$
D $(2 - \sqrt{2}) p s q c m$

NCERT EXEMPLAR-HERON'S FORMULA-Herons Formula

Home
Ask Doubt
Profile