The area of the region bounded by parabola y2=x and the straight line 2y=x is
43sq units
1 sq unit
23 sq unit
13 sq units
The correct Answer is:A
We have to find the area enclosed by parabolay2=x and the straight line 2y=x.
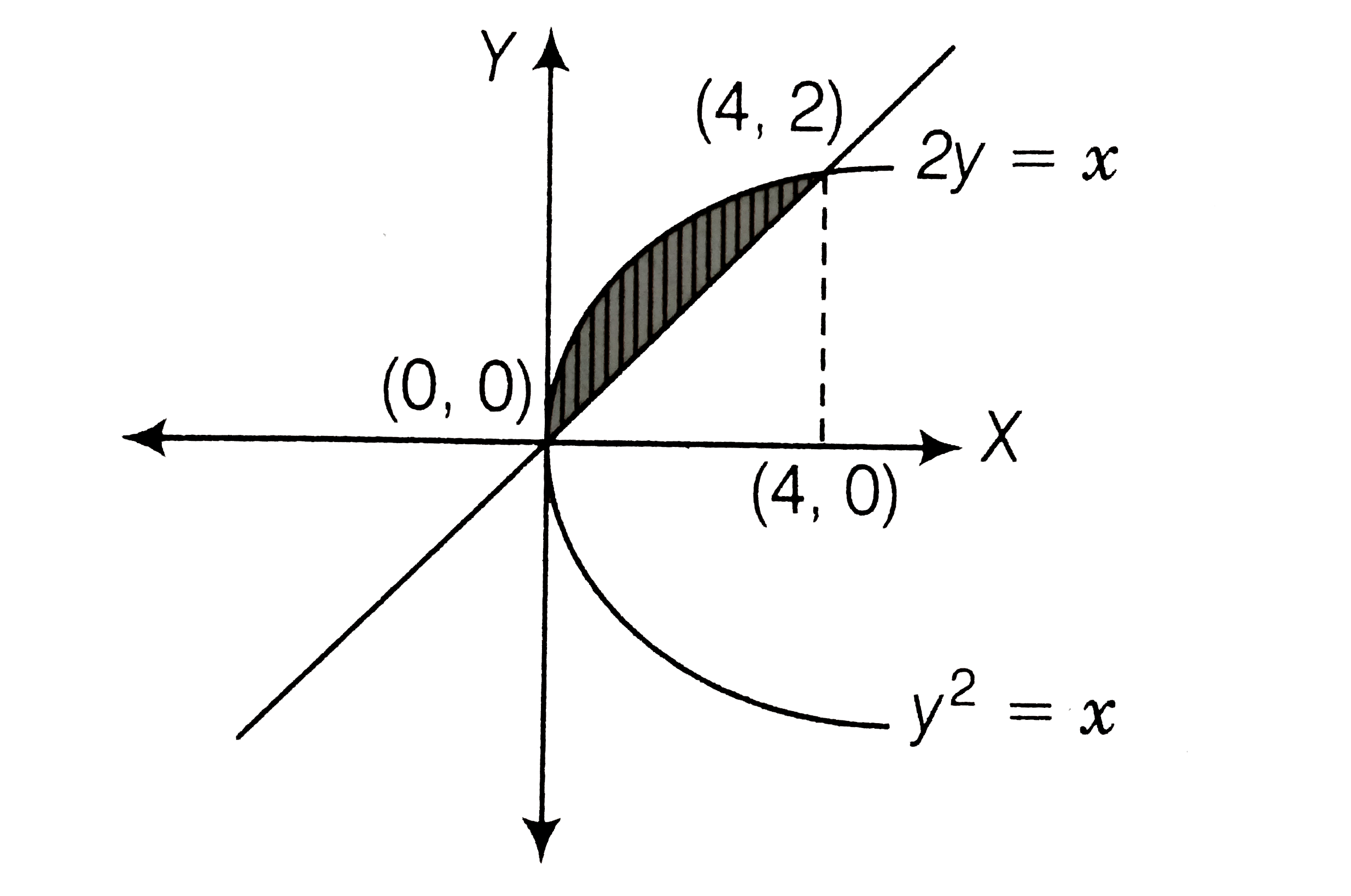
∴(x−2)2=x
⇒x2=4x⇒x(x−4)=0
⇒x=4⇒y=2 and x=0⇒y=0
So, the intersection points are (0,0) and (4,2).
Area enclosed by shaded region,
A=∫40[√x−x2]dx
=⎡⎣c12+112+1−12.x22⎤⎦40=[2.x3/23−x24]40
=2343/2−164−23.0+14.0
=163−164=64−4812=1612=43 sq units
Related Playlists
Similar Questions
The area of the region bounded by the parabola y=x2−4x+5 and the straight line y=x+1 is
View SolutionThe area of the region bounded by the parabola y2=9x and the line y=3x is :
View SolutionThe area of the region enclosed by the parabola y=2−x2 and the straight line y=−x is equal to:
View SolutionFind the area of the region bounded by the parabola y2=2x and straight line x−y=4.
View SolutionThe area of the region bounded by the parabola x=−y2 and the line y=x+2 is
View SolutionFind the area of the region bounded by the parabola y2=2x and the line x−y=4
View SolutionThe area of the region bounded by the parabola y=x2 and the line y = 4x is
View SolutionFind the area of the region bounded by: the parabola y=x2 and the line y=x
View SolutionFind the area of the region bounded by the parabola y2=8x and the line x=2
View SolutionUsing integration, find the area of the region bounded by the parabola y2=4x and the line x=4.
View Solution


