The area bounded by the curves and lines x = 1 and y = 4a is
sq units
sq units
sq units
None of these
The correct Answer is:B
On solving and y=4a, we get x = 5
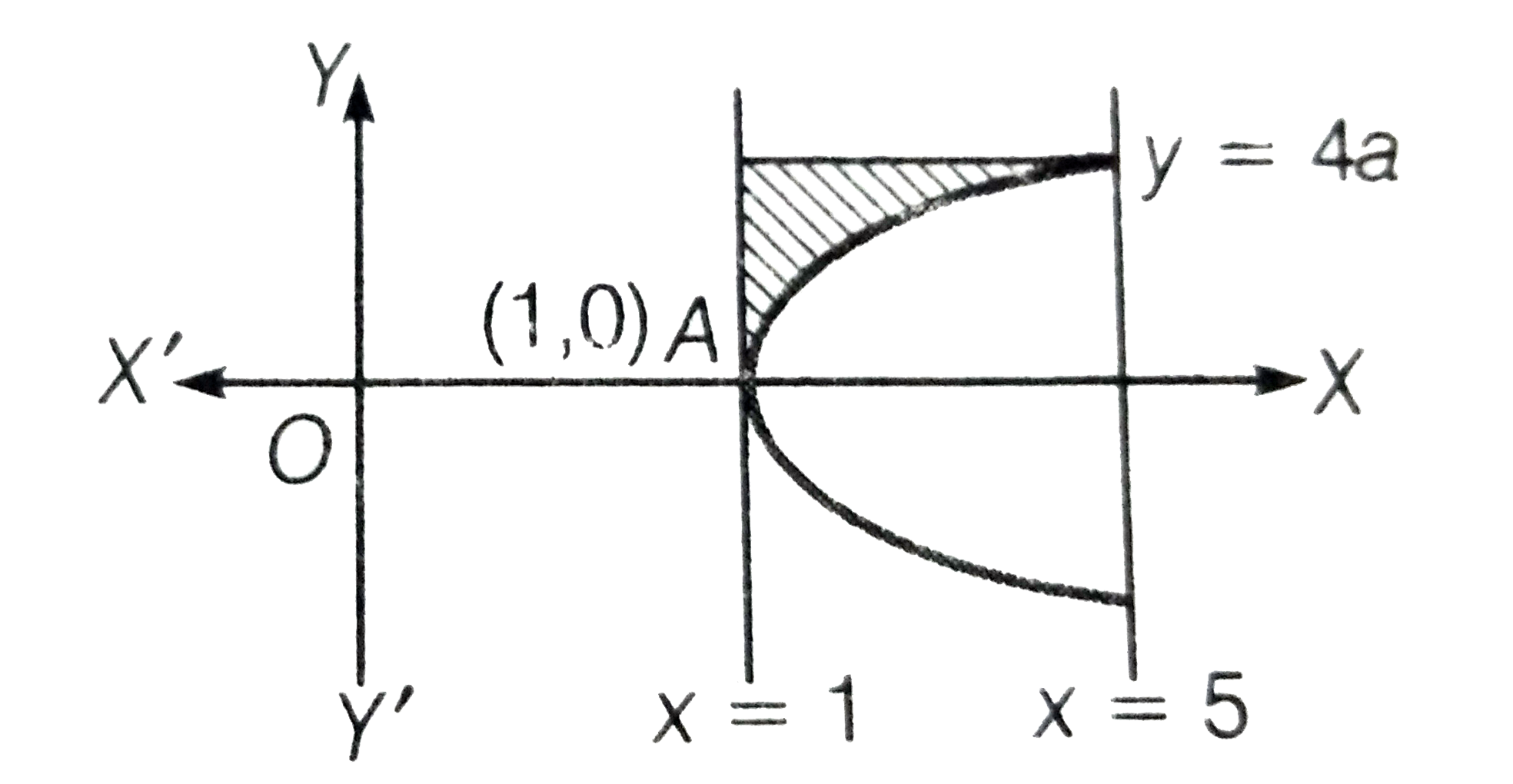
Required area
sq units
Related Playlists
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner6videos
APPLICATIONS OF DEFINITE INTEGRALS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner6videos
APPLICATIONS OF DEFINITE INTEGRALS
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER21videos
APPLICATIONS OF DERIVATIVES
Similar Questions
The area of the region bounded by the curves y2=4a2(x−1) and the lines x = 1 and y = 4a, is
View SolutionThe area bounded by the curves y2=4x and x2=4y
View SolutionThe area bounded by the curve y=x(x2−1) and x-axis is
View SolutionThe area bounded by the curve y2=16x and the line x = 4 is
View SolutionThe area bounded by the curve y2=14x and the lines x = 1, x = 4 above X-axis is
View SolutionThe area bounded by the curve y2=8x and the line x=2 is
View SolutionThe area bounded by the curve y2=9x and the lines x=1,x=4andy=0, in the first quadrant,is
View SolutionFind the area bounded by the curves : y2=4x,y2=x,x=1andx=4
View SolutionThe area bounded by the curve y2=4x and the line 2x−3y+4=0 is
View SolutionThe area bounded by the curve x2=4y+4 and line 3x+4y=0 is
View Solution


