The area of the region bounded by the curves y2=4a2(x−1) and the lines x = 1 and y = 4a, is
A
21a2 sq unit
B
163 sq unit
C
17a3 sq unit
D
16a3 sq unit
Video Solution
Text Solution
The correct Answer is:D
We have,
y2=4a2(x−1)
⇒(y−0)2=4a2(x−1)
Clearly, this equation represents a parabola with vertex at (1, 0) as shown in figure. The area enclosed by y2=4a2(x−1),x=1 and y=4a is the area of shaded portion in figure.
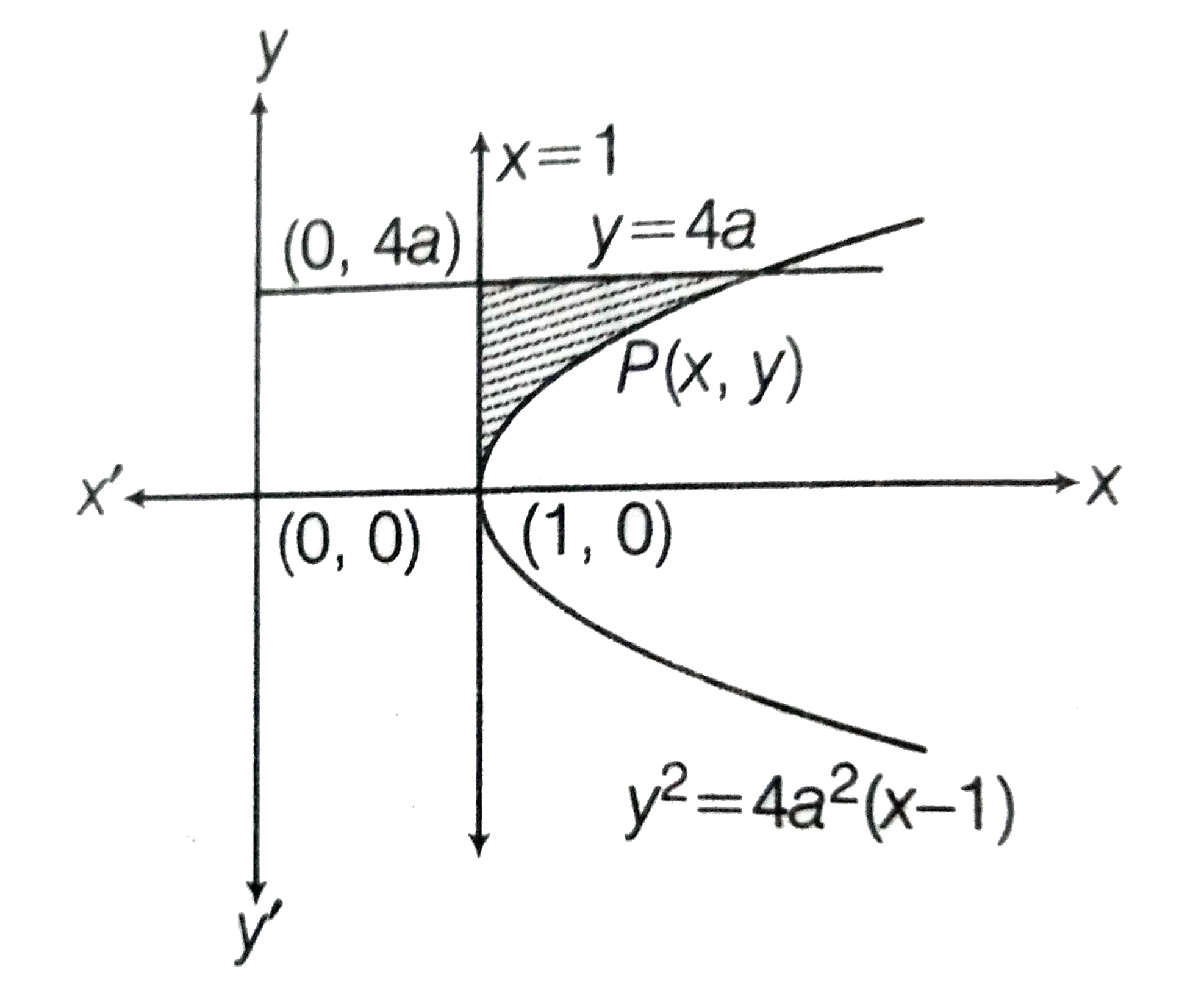
=∫4a0(x−1)dy
=∫4a0y24a2dy [∵P(x,y)lies on y2=4a2(x−1)∴x−1=y2/4a2]
=14a2[y33]4a0
=14a2(64a33)=16a3 sq unit
|
Topper's Solved these Questions
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - Exercise 2
34 Videos
- APPLICATIONS OF DEFINITE INTEGRALS BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DEFINITE INTEGRALS EXERCISE - MHT CET Corner
6 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - MHT CET CORNER
21 Videos
Similar Questions
Knowledge Check
The area bounded by the curves y2=4a2(x−1) and lines x = 1 and y = 4a is
A4a2 sq unitsB16a3 sq unitsC16a23 sq unitsDNone of theseThe area of the region bounded by the curve y=x2 and the line y=16 is :
A323B2563C643D1283The area of the region bounded by the curves x=y2−2 and x=y is
A94B9C92D97
Find the area of the region bounded by the curve y=x2and the line y=4.
View SolutionFind the area of the region bounded by the curve y=x2 and the line y=4.
View SolutionThe area of the region bouned by the curve y=2x−x2 and the line y=x is
View SolutionThe area of the region bounded by the circle x2+y2=1 and the line x+y=1 is :
View SolutionArea of the region bounded by the curve y2= 4x , y-axis and the line y = 3 is (A) 2 (B) 94 (C) 93 (D) 92
View Solution
