In the given figure, L and M are the midpoints of two equal chords AB and CD of a circle C(O,r).
Prove that (i) ∠OLM=∠OML
(ii) ∠ALM=∠CML.
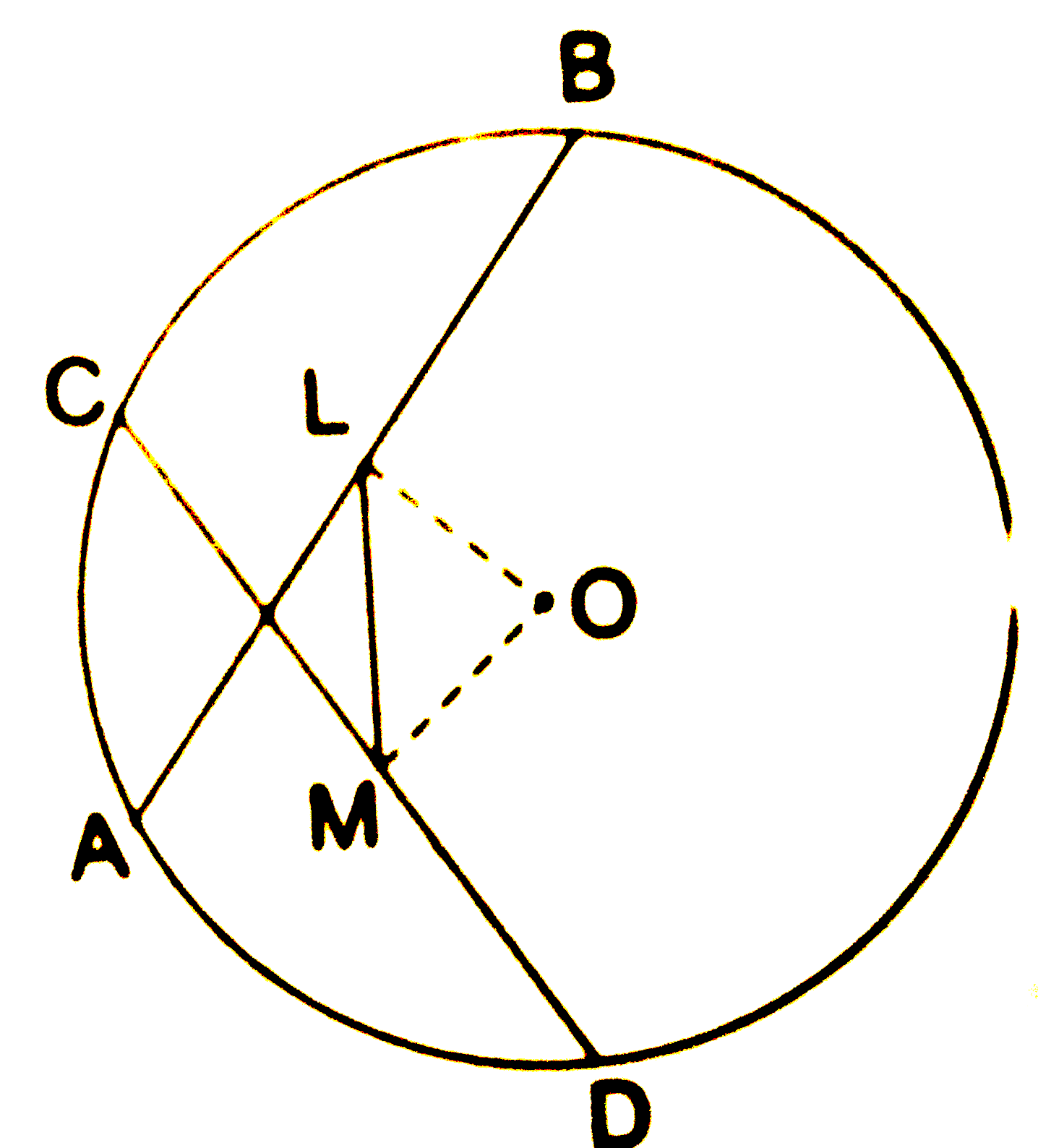
Proof Since L is the midpoint of chord AB, we have OL⊥AB.
Again, M is the midpoint of chord CD.
∴OM⊥CD
But, equal chords of a circle are equidistant from the centre.
∴AB=CD⇒OL=OM
⇒∠OLM=∠OML ...(i)
Now, ∠ALM=∠OLA−∠OLM=90∘−∠OLM
∠CML=∠OMC−∠OML=90∘−∠OML.
But ∠OLM=∠OML [ from (i) ],
∴∠ALM=∠CML
Topper's Solved these Questions
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:Exercise 12A
Explore 22 Videos
- CIRCLES Book:RS AGGARWALChapter:CIRCLES Exercise:EXERCISE 12B
Explore 18 Videos
- BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONBook:RS AGGARWALChapter:BAR GRAPH, HISTOGRAM AND FREQUENCY POLYGONExercise:EXERCISE 17B
Explore 16 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBook:RS AGGARWALChapter:CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEExercise:Multiple Choice Questions (Mcq)
Explore 20 Videos
Similar Questions
L and M are mid-point of two equal chords AB and CD of a circle with centre O . Prove that ∠OLM= ∠OML (ii) ∠ALM= ∠CML
View SolutionL and M are mid points of two equal chords AB and CD of a circle with center O. Prove that ∠OLM=∠OML and ∠ALM=∠CML
View SolutionIn the given figure. AB∣CDandO is the midpoint of AD.
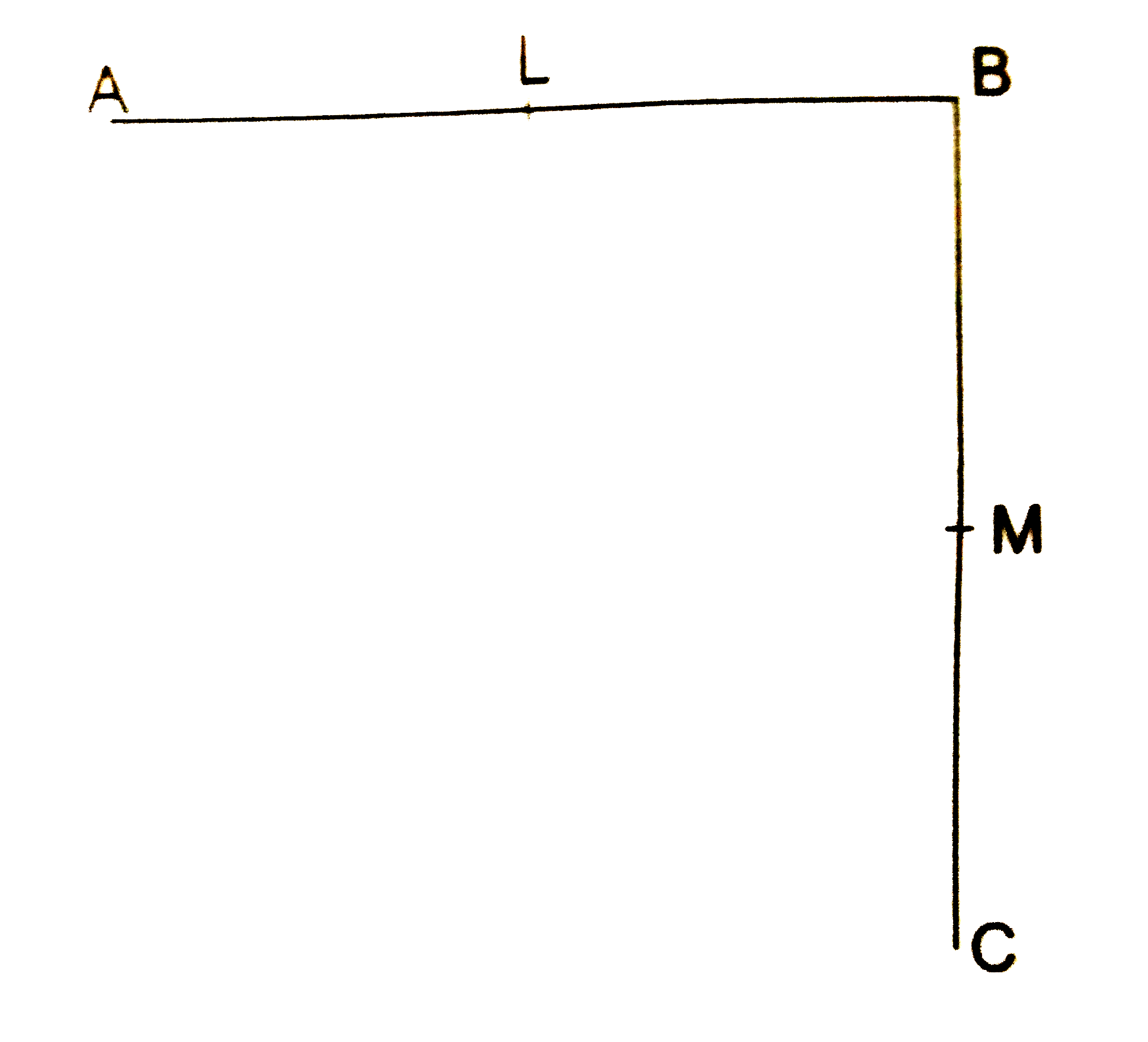
View SolutionIn the given figure L and M are the midpoints of AB and BC respectivcely
(i) If AB= BC prove that AL = MC
(ii) If BL = BM prove that AB=BC
View SolutionIn the given figure,AB and CDare equal chords of a circle with centre O .Prove that ∠AOB≅∠COD and ∠AOB=∠COD
View SolutionIn the figure, two equal chords AB and CD of a circle with centre O, intersect each other at E, Prove that AD=CB
View SolutionIn the given figure, P is the mid-point of arc APB and M is the mid-int of chord AB of a circle with centre O. Prove that PM⊥AB
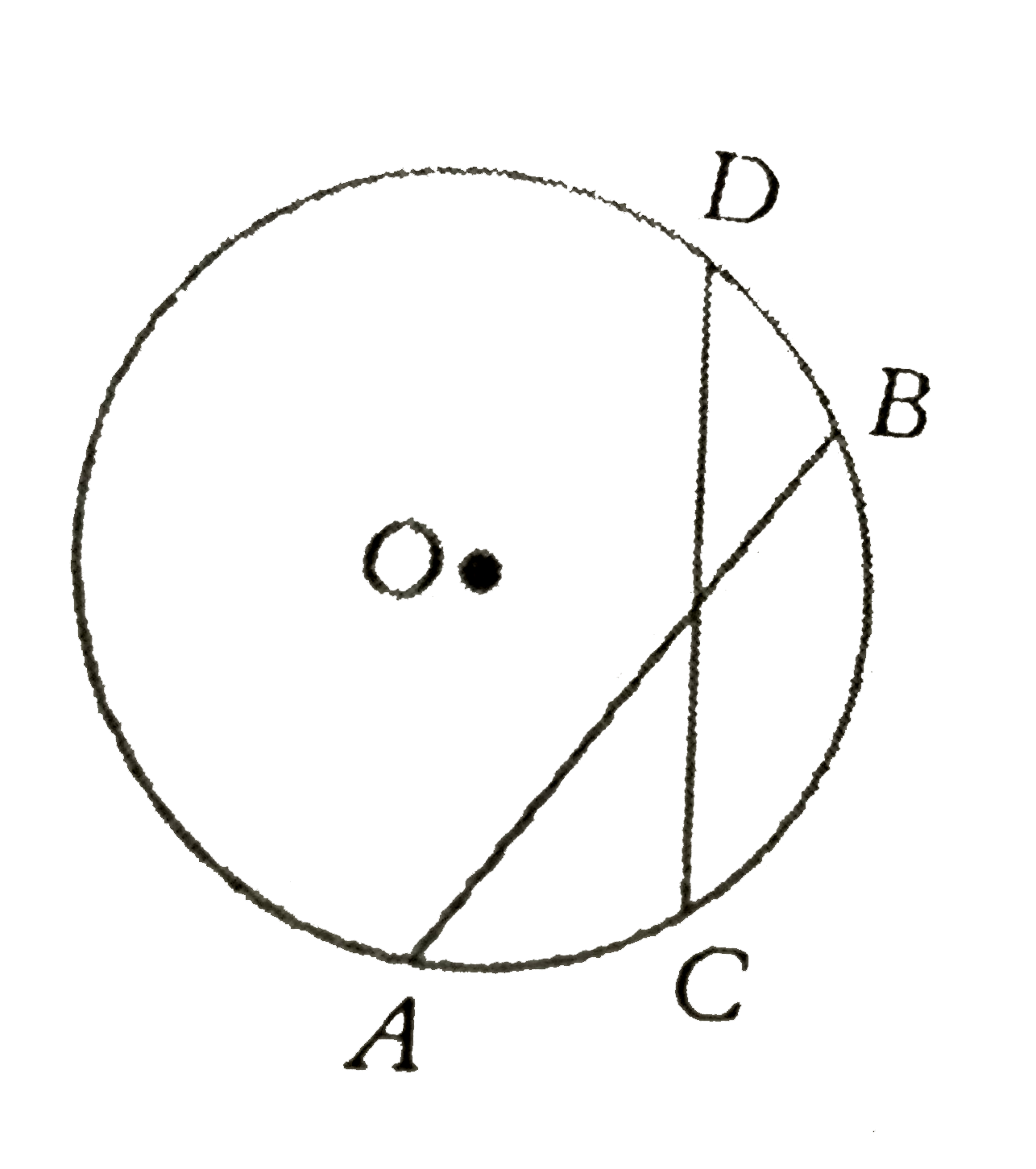
View SolutionIn the given figure, AB and CD are two equal chords. If O is the centre of the circle , ∠AOB=120∘, then find ∠OCD.
View SolutionIn the given figure, AB and AC are two equal chords of a circle with centre O. Show that O lies on the bisectors of ∠BAC.
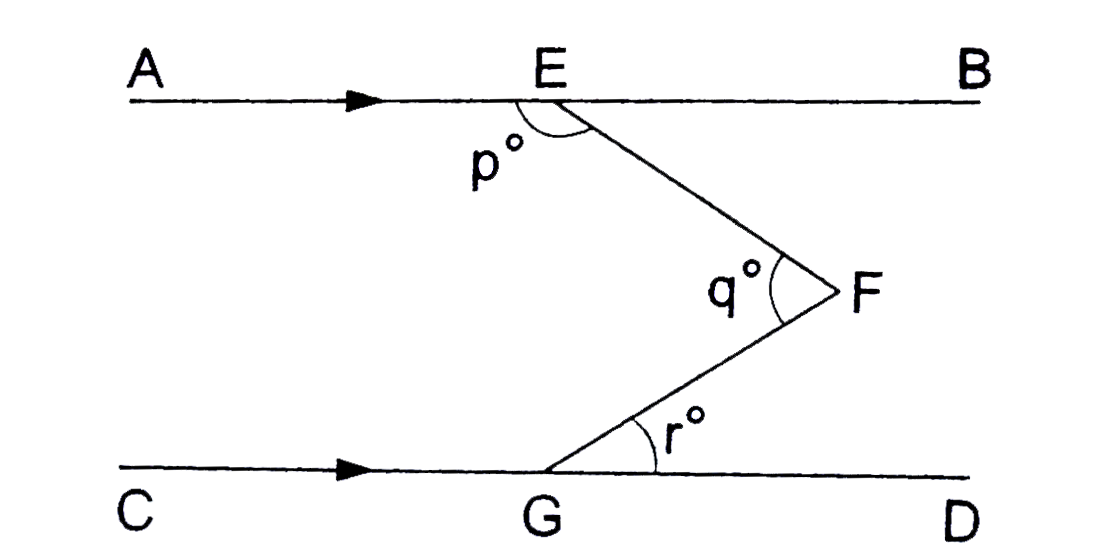
View SolutionIn the given figure, AB∣∣CD. Prove that p+q−r=180.
View Solution

