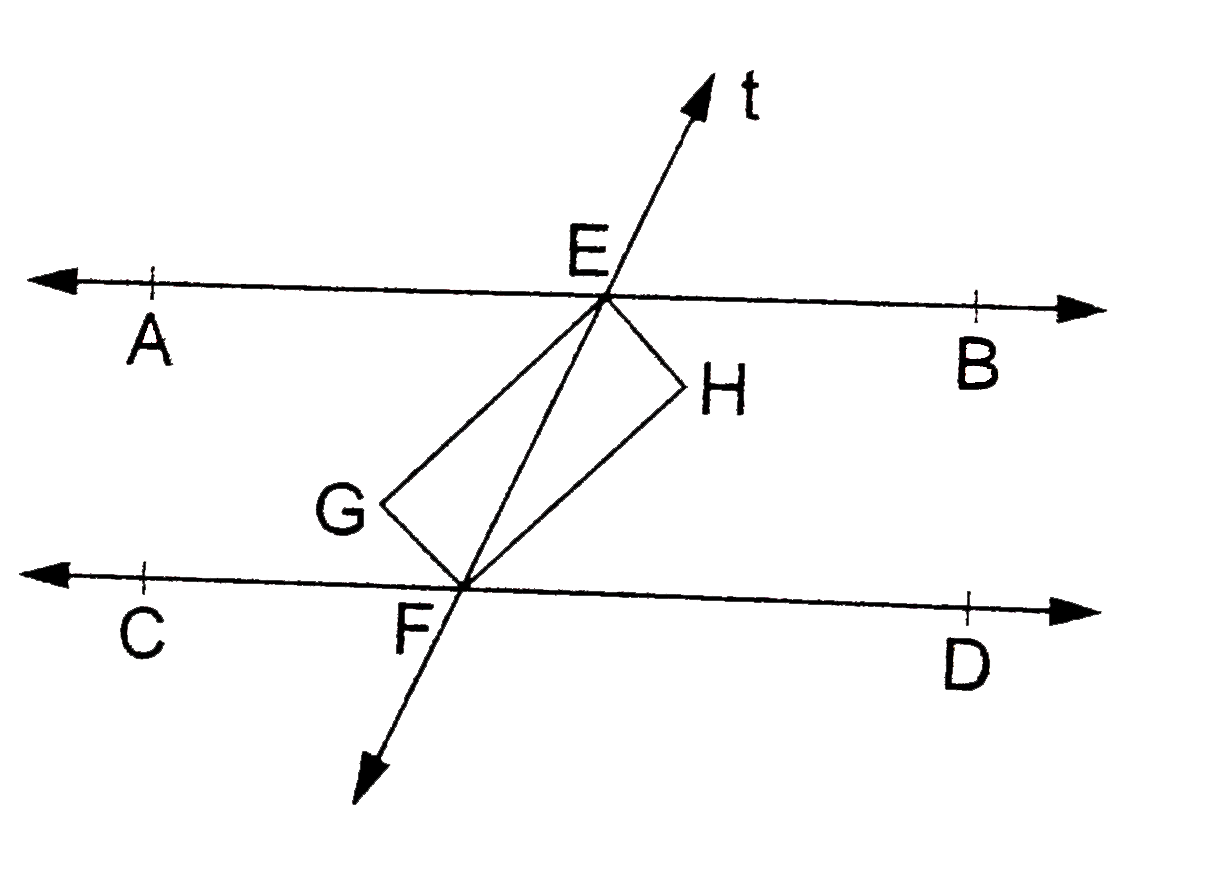
If two parallel lines are intersected by a transversal, prove that the bisectors of the two pairs of interior angles enclose a rectangle.
GIVEN AB∣∣CD and a transversal t cuts them at E and F respectively. EG, FG, EH and FH are the bisectors of the interior angles ∠AEF,∠CFE,∠BEF and ∠EFD respectively.
TO PROVE EGFH is a rectangle.
PROOF AB∣∣CD and the transversal t cuts them at E and F respectively.
∴∠AEF=∠EFD [alt. int. ∠s]
⇒1.2∠AEF=1.2∠EFD⇒∠GEF=∠EFH.
But, these are alternate interior angles formed when the transversal EF cuts EG and FH.
∴EG∣∣FH. Similarly, EH∣∣FG.
∴ EGFH is a parallelogram.
Now, ray EF stands on line AB.
∴∠AEF+∠BEF=180∘ (linear pair)
⇒12∠AEF+12∠BEF=90∘⇒∠GEF+∠HEF=90∘
⇒∠GEH=90∘ [∵∠GEF+∠HEF=∠GEH].
Thus, EGFH is a parallelogram, one of whose angles is 90∘. Hence, EGFH is a rectangle.
Related Playlists
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Example13videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINES AND ANGLESEXERCISE - Exercise 7A12videos
LINES AND ANGLES
- BOOK - RS AGGARWALCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Multiple Choice Questions (Mcq)24videos
LINEAR EQUATIONS IN TWO VARIABLES
- BOOK - RS AGGARWALCHAPTER - MEAN , MEDIAN AND MODE OF UNGROUPED DATA EXERCISE - Multiple Choice Questions (Mcq)18videos
MEAN , MEDIAN AND MODE OF UNGROUPED DATA
Similar Questions
If two parallel lines intersected by a transversal; prove that the bisectors of the two pairs of interior angle encloses a rectangle.
View SolutionIf two parallel lines are intersected by a transversal then prove that the bisectors of any pair of alternate interior angles are parallel.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two parallel lines are intersected by a transversal, prove that the bisectors of the interior angles on the same side of transversal intersect each other at right angles.
View SolutionIf two lines are intersected by a transversal; the bisectors of any pair of alternate interior angles are parallel.
View SolutionIf two parallel lines are intersected by a transversal; the bisector of any two corresponding angles are parallel.
View SolutionIf two parallel lines are intersected by a transversal , then the interior angles on the same side of the transversal are -
View SolutionTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
 View Solution
View SolutionIf two lines are intersected by a transversal, then the number of pairs of interior angles on the same side of the transversal is
View SolutionAB,CD are two parallel lines and a transversal l intersects AB at X and CD at Y Prove that the bisectors of the interior angles form a parallelogram, with all its angles right angles i.e., it is a rectangle.
View Solution


