If (b2−b1)(b3−b−1)+(a2−a1)(a3−a1)=0, then prove that the circumcenter of the triangle having vertices (a1,b1),(a2,b2) and (a3,b3) is (a2+a32,b2+b32).
Video Solution
Text Solution
Given (b2−b1)(b3−b1)+(a2−a1)(a3−a1)=0
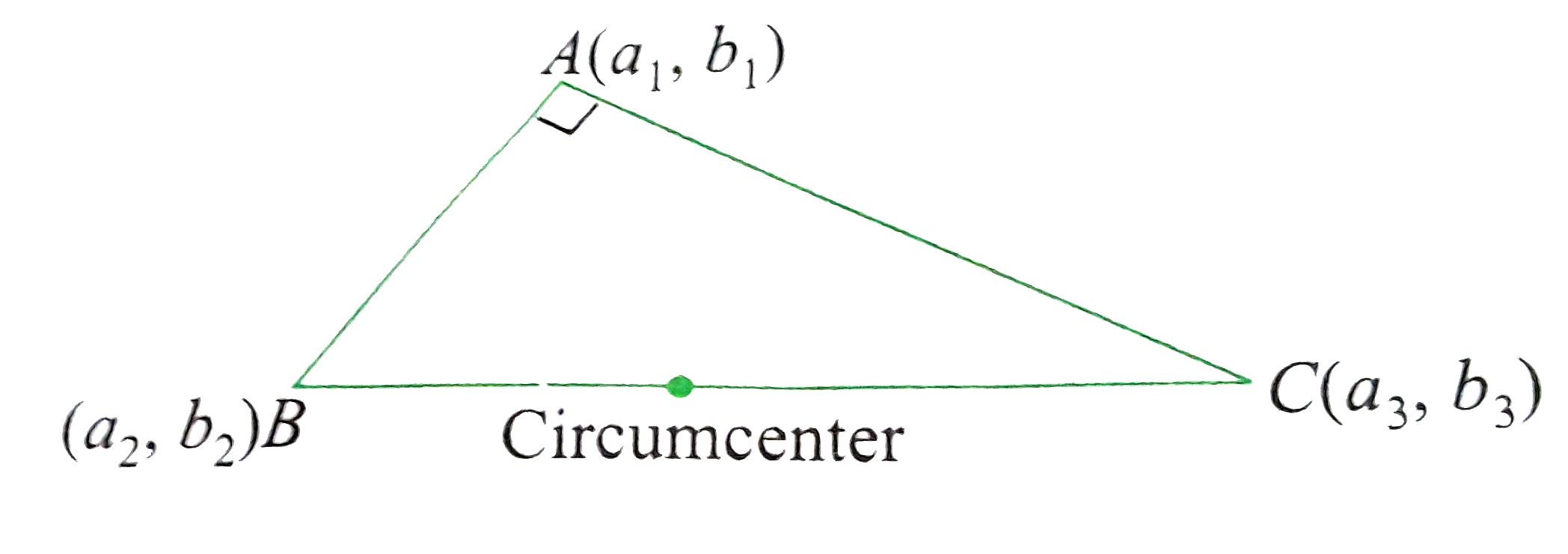
or (b2−b1)(b3−b1)=−(a2−a1)(a3−a1)
or (b2−b1a2−a1)(b3−b1a3−a1)=−1
or (slope of AB)×(slope of AC)=−1
Therefore, the triangle is right -angled at point (a1,b2). Hence, the circumcenter is the midpoint of (a2b2) and (a3,b3) which is (a2+a32,b2+b32)
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.16videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSYEM EXERCISE - Exercise 1.28videos
COORDINATE SYSYEM
- BOOK - CENGAGECHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type2videos
COORDINATE SYSTEM
- BOOK - CENGAGECHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.213videos
CROSS PRODUCTS
Similar Questions
Knowledge Check
- Question 1 - Select One
∣∣ ∣ ∣∣x1y11x2y21x3y31∣∣ ∣ ∣∣=∣∣ ∣∣a1b11a2b21a3b31∣∣ ∣∣ then the two triangles with vertices (x1,y1),(x2,y2),(x3,y3)and(a1,b1),(a2,b2),(a3,b3) are
Aequal in areaBsimilarCcongruentDNone of these - Question 2 - Select One
If the equation of the locus of a point equidistant from the points (a1,b1) and (a2,b2) is (a1−a2)x+(b2+b2)y+c=0, then the value of C is
Aa21−a22+b21−b22B√a21+b21−a22−b22C12(a21+a22+b21+b22)D12(a21+b22+a21+b22)
Prove by vector method that (a1b1+a2b2+a3b3)2<+(a21+a22+a23)(b21+b22+b23)
View SolutionIn direct proportion a1b1 = a2b2
View SolutionProve that the value of each the following determinants is zero: ∣∣ ∣∣a1la1+mb1b1a2la2+mb2b2a3la3+mb3b3∣∣ ∣∣
View Solution∣∣ ∣∣1+a1a2a3a11+a2a3a1a21+a3∣∣ ∣∣=1+a1+a2+a3.True or False .
View SolutionThe determinant ∣∣ ∣∣b1+c1c1+a1a1+b1b2+c2c2+a2a2+b2b3+c3c3+a3a3+b3∣∣ ∣∣=
View SolutionThe equation Ax−a1+A2x−a2+A3x−a3=0whereA1,A2,A3>0anda1<a2<a3 has two real roots lying in the invervals. (A) (a1,a2)and(a2,a3) (B) (−∞,a1)and(a3,∞) (C) (A1,A3)and(A2,A3) (D) none of these
View Solution
