If a man standing on a platform 3 m above the surface of a lake observes a cloud and its reflection in the lake, then the angle of elevation of the cloud is equal to the angle of depression of its reflection.
False,
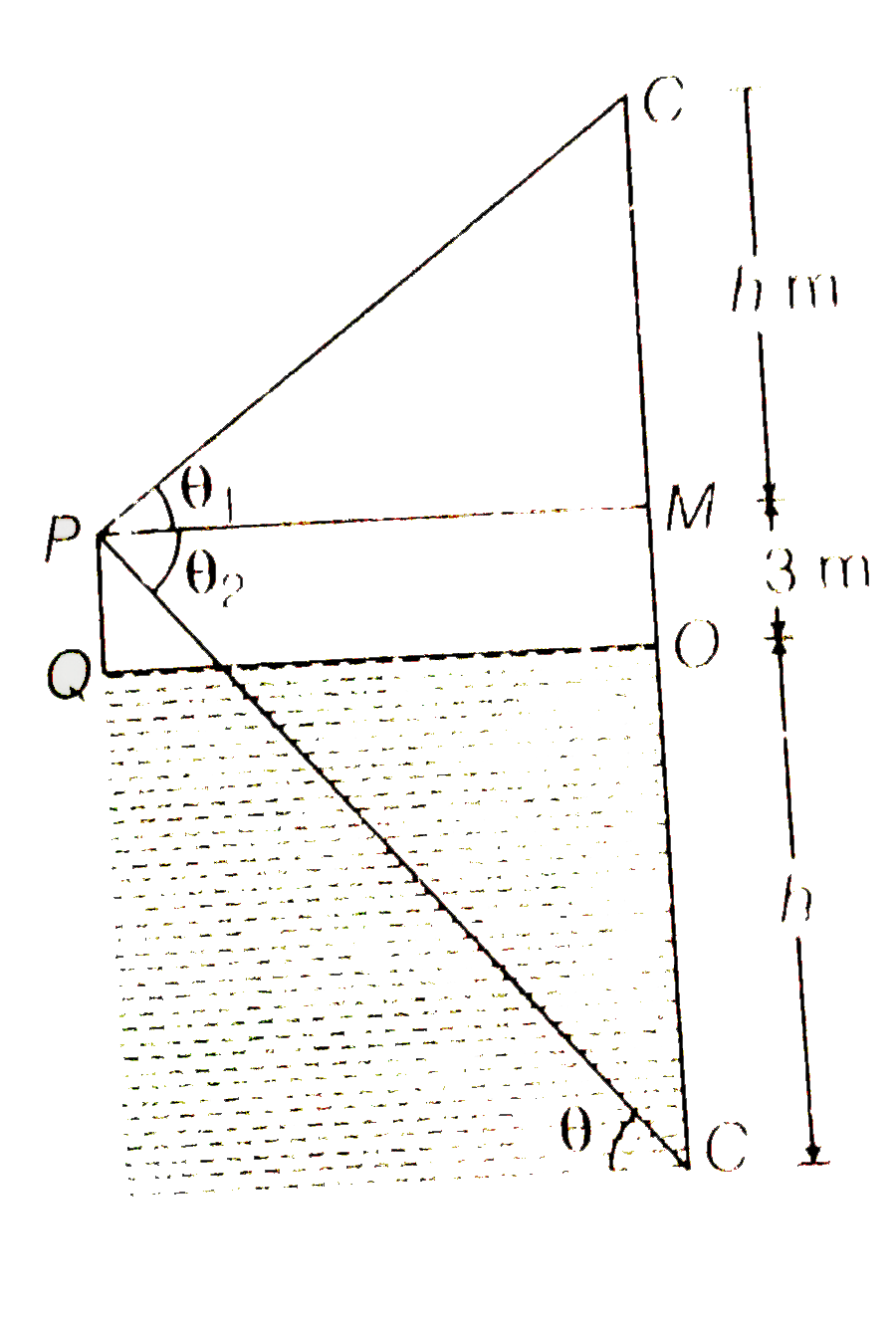
From figure, we observe that, a man standing on a platform at point P, 3 m above the surface of a lake observes a cloud at point C. Let the height of the cloud from the surface of the platfom is h and angle of elevatin of the cloud is θ1.
Now at same point P a man observes a cloud reflection in the lake at this time the height of reflection of cloud in lake is (h+3) because in lake platform height is also added to reflection of cloud.
So, angle of depression is different in the lake from the angle of elevatino of the cloud above the surface of a lake.
In ΔMPC,tanθ1=CMPM=hPM
⇒tanθ1h=1PM..................(i)
In ΔCPM,tanθ2=CMPM=OC+OMPM=h+3PM
⇒tanθ2h+3=1PM...........(ii)
From eqs. (i) and (ii),
tanθ1h=tanθ2h+3
⇒tanθ2=h+3htanθ1
Hence, θ1≠θ2
Alternate method:
False, we know that, if P is a point above the lake at a distance d, then the reflection of the point in the lake would be at the same distance d. Also, the angle of elevation and depression from the surface of the lake is same.
Here, the man is standing on a platform 3m above the surface, so its angle of elevation to the cloud and angle of depression to the reflection of the cloud is not same.
Related Playlists
Similar Questions
A helicopter is in a stationary position at a certain height over the lake. At a point 200 m above the surface of the lake, the angle of elevation of the helicopter is 45∘. At the same time, the angle of depression of its reflection in the lake is 75∘. Calculate the height of the helicopter from the surface of the lake :
View SolutionThe angle of elevation of a cloud from a point h meter above the surface of the lake is α, the angle of depression of its reflection in the lake is β. Prove that height of the cloud from observation points is 2hsecαtanβ−tanα.
View SolutionAman on deck of a ship is 12 m above the water level. He observes that the angle of the elevation of the top of a cliff is 45∘ and the angle of depression of its base is 30∘. Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionA man on the deck of a ship is 10m above the water level. He observes that the angle of elevation of the top of a cliff is 45o and the angle of depression of the base is 30o . Calculate the distance of the cliff from the ship and the height of the cliff.
View SolutionThe angle of elevation of a cloud from a point h metre above a lake is θ.The angle depression of its reflection in the lake is 45∘The height of the cloud is
View SolutionThe angle of elevation of a cloud from a point h m above the level of water in a lake is α and the angle of depression of its reflection in the lake is β. Then the height of the cloud above the water level is
View SolutionA man standing on the deck of a ship, which is 10m above water level. He observes the angle of elevation of the top of a hill as 600 and the angle of depression of the base of the hill as 300. Calculate the distance of the hill from the ship and the height of the hill.
View SolutionA man standing on the deck of a ship, which is 8m above water level. He observes the angle of elevation of the top of a hill as 60o and the angle of depression of the base of the hill as 30o . Calculate the distance of the hill from the ship and the height of the hill.
View SolutionIf the angle of elevation of a cloud from a point 200m above a lake is 30∘ and the angle of depression of its reflection in the lake is 60∘ .Then the height of the cloud above the lake is :
View SolutionThe angle of elevation of a cloud from a point h mt. above is θ∘ and the angle of depression of its reflection in the lake is ϕ. Then, the height is
View Solution


