If $tan A = \frac{3}{4}$ , then $sin A cos A =$ .

A

$\frac{12}{24}$

B

$\frac{12}{25}$

C

$\frac{9}{25}$

D

$\frac{16}{25}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

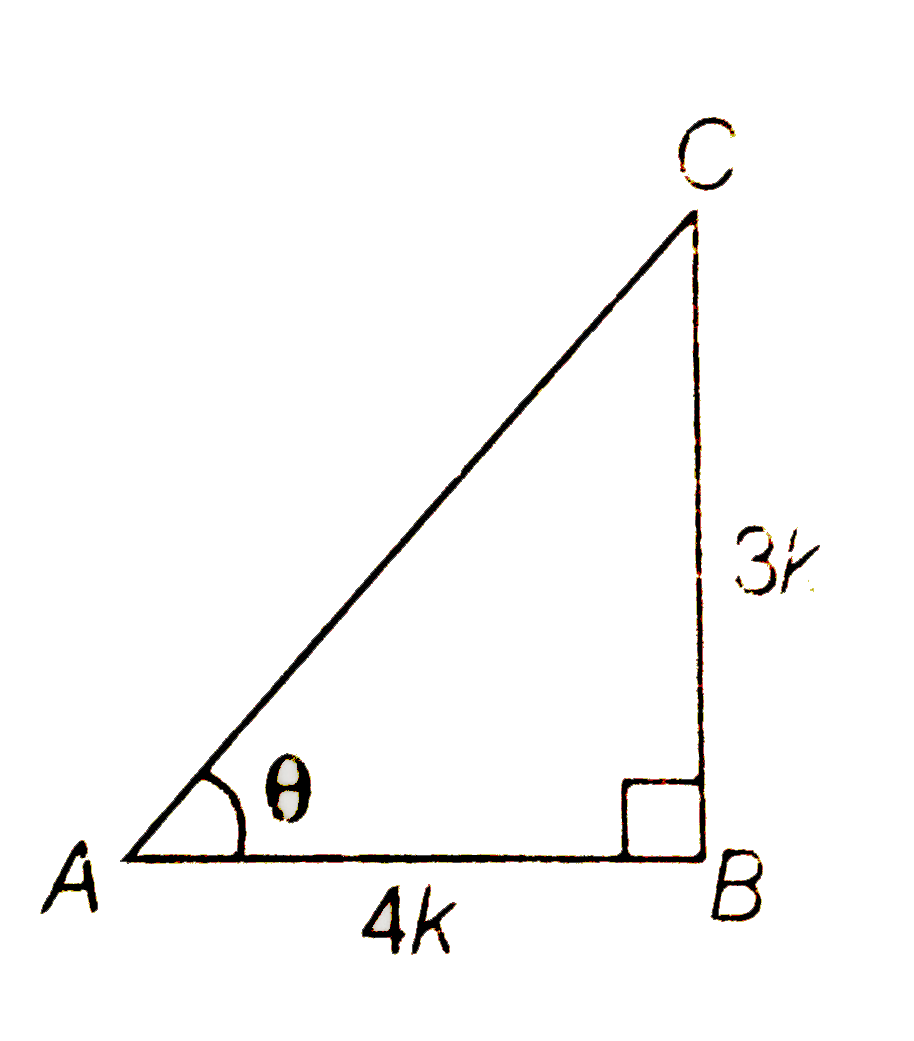
Given, $tan A = \frac{3}{4} = \frac{P}{B} = \frac{Perpendicular}{Base 0}$
Let P=3k and B=4k
By pythagoras theorem,
$H^{2} = P^{2} + B^{2} = {(3 K)}^{2} + {(4 k)}^{2}$
$= 9 k^{2} + 16 k^{2} = 25 k^{2}$
$\Rightarrow H = 5 k$ (since, side cannot be negative)
$∴ sin A = \frac{P}{H} = \frac{3 k}{5 k} = \frac{3}{5}$ and $cos A = \frac{B}{H} = \frac{4 k}{5 k} = \frac{4}{5}$
Now, sinAcosA= $\frac{3}{5.4} / 5 = \frac{12}{25}$

Updated on:21/07/2023

|

Class 10 MATHS TRIGONOMETRIC RATIOS AND IDENTITIES

Topper's Solved these Questions

Similar Questions

Knowledge Check

If $sec θ + tan θ = \frac{4}{3}$ , then $sec θ tan θ$ =_______
A $\frac{175}{24}$
B $\frac{25}{576}$
C $\frac{27}{576}$
D $\frac{175}{576}$
$tan (\frac{π}{4} + θ) tan (\frac{3 π}{4} + θ)$ is equal to
A $- 2$
B $- 1$
C1
D0

NCERT EXEMPLAR-INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONS-Introduction To Trigonometry And Its Applications

Home
Ask Doubt
Profile