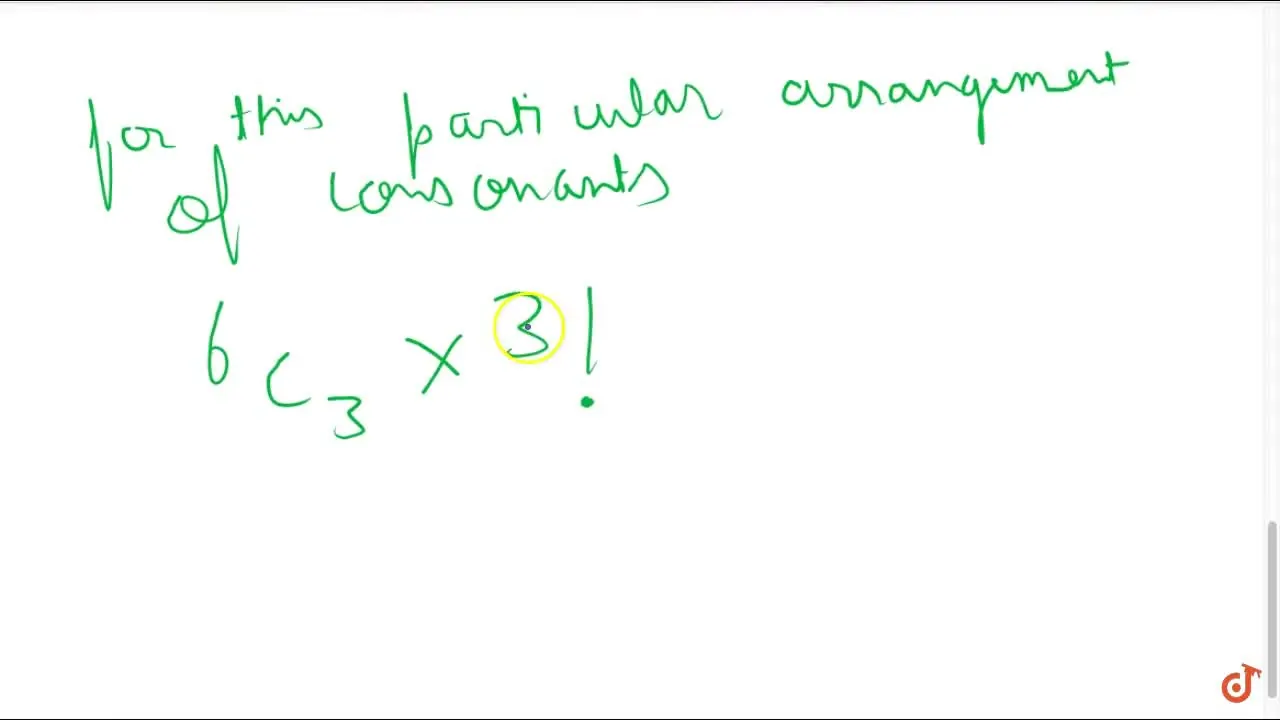How many words can be formed form the letters of the word DAUGHTER so that The vowels always come together? The vowels never come together?
The letters of the word daughter are “d,a,u,g,h,t,e,r”.
So, the vowels are ‘a, u, e’ and the consonants are “d,g,h,t,r”.
(i)Now, all the vowels should come together, so consider the bundle of vowels as one letter, then total letters will be 6.
So, the number of words formed by these letters will be 6!
but, the vowels can be arranged differently in the bundle, resulting in different words, so we have to consider the arrangements of the 3 vowels.
So, the arrangements of vowels will be 3!
Thus, the total number of words formed will be equal to (6!×3!)=4320
(ii)First arrange 5 consonants in five places in 5! ways.
6 gaps are created. Out of these 6 gaps, select 3 gaps in 6C3 ways and then make the vowels permute in those 3 selected places in 3! ways.
This leads 5!×6C3×3!=14400.
Related Playlists
Similar Questions
How many words can be formed by arranging the letters of the word 'INDIA', so that the vowels are never together?
View SolutionHow many words can be made out of the letters of the word INDEPENDENCE in which vowels always come together ?
View SolutionHow many diferent words can be formed with the letters of the word VICE-CHANCELLOR so that the vowels are together?
View SolutionHow many words can be formed by arranging the letters of the word 'ARRANGEMENT', so that the vowels remian together?
View SolutionHow many words can be formed with the letters of the words ‘ORDINATE’ so the vowels occupy odd places?
View SolutionHow many words can be formed with the letters of the word 'GUJRAT', if all vowels are always together?
View SolutionHow many different words can be formed with the letters of the word REGURGITATE so that the two T's are always together?
View SolutionHow many words can be formed out of the letters of the word, ARTICLE, so that vowels occupy even places?
View SolutionHow many words can be formed using all the letters of the word 'NATION' so that all three vowels should never together?
View SolutionHow many words can be formed out of the letters of the word, ORIENTAL, so that the vowels always occupy the odd places?
View Solution