Question

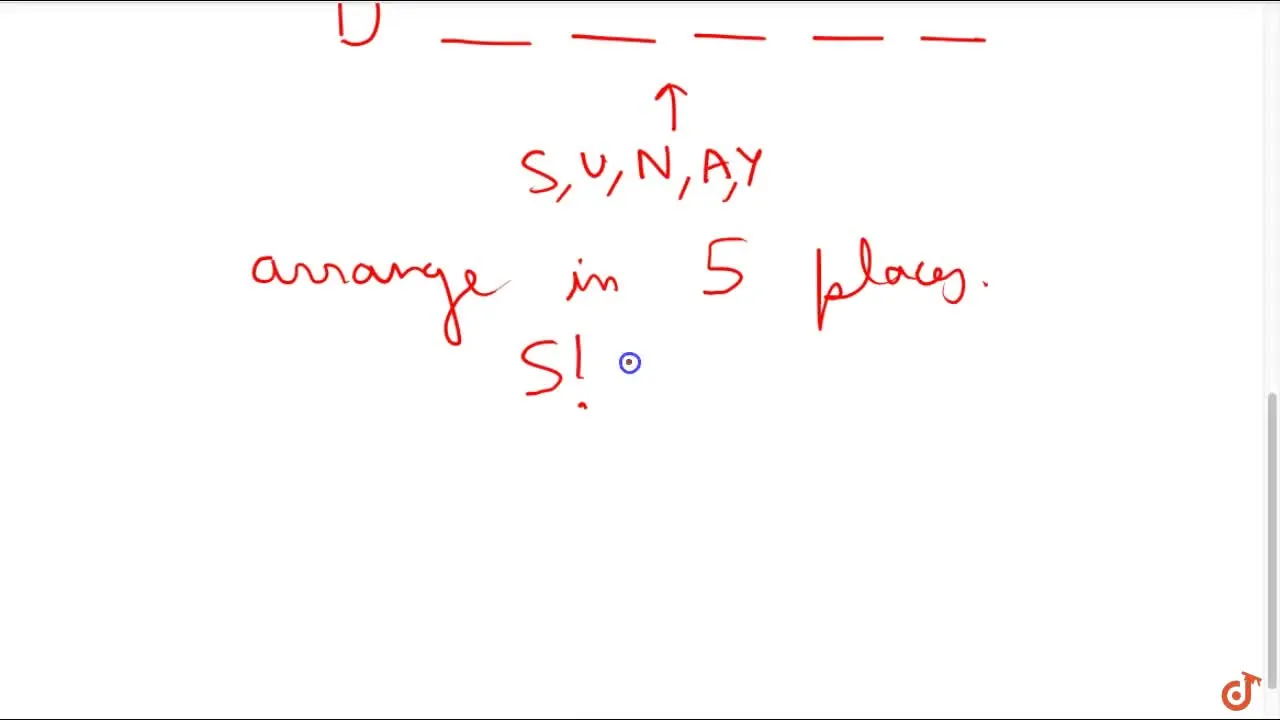
How many words can be formed from the letters of the word SUNDAY? How
many of these begin with D?

Explanation

To solve the problem, we need to find two things:

1. The total number of words that can be formed using the letters of the word "SUNDAY".
2. The number of those words that begin with the letter "D".

Step 1: Calculate the total number of arrangements of the letters in "SUNDAY".

The word "SUNDAY" consists of 6 distinct letters: S, U, N, D, A, Y.

To find the total number of arrangements of these 6 letters, we use the formula for permutations of n distinct objects, which is given by n! (n factorial).

Here, n = 6 (since there are 6 letters).

So, the total number of arrangements is:
\( 6! = 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720 \)

Step 2: Calculate the number of arrangements that begin with the letter "D".

If we want the arrangements to start with "D", we fix "D" in the first position. This leaves us with the letters S, U, N, A, and Y to arrange.

Now, we have 5 letters left (S, U, N, A, Y), and we need to find the number of ways to arrange these 5 letters.

Using the same formula for permutations, we calculate:
\( 5! = 5 \times 4 \times 3 \times 2 \times 1 = 120 \)

Final Answer:

1. The total number of words that can be formed from the letters of "SUNDAY" is 720.
2. The number of words that begin with "D" is 120.