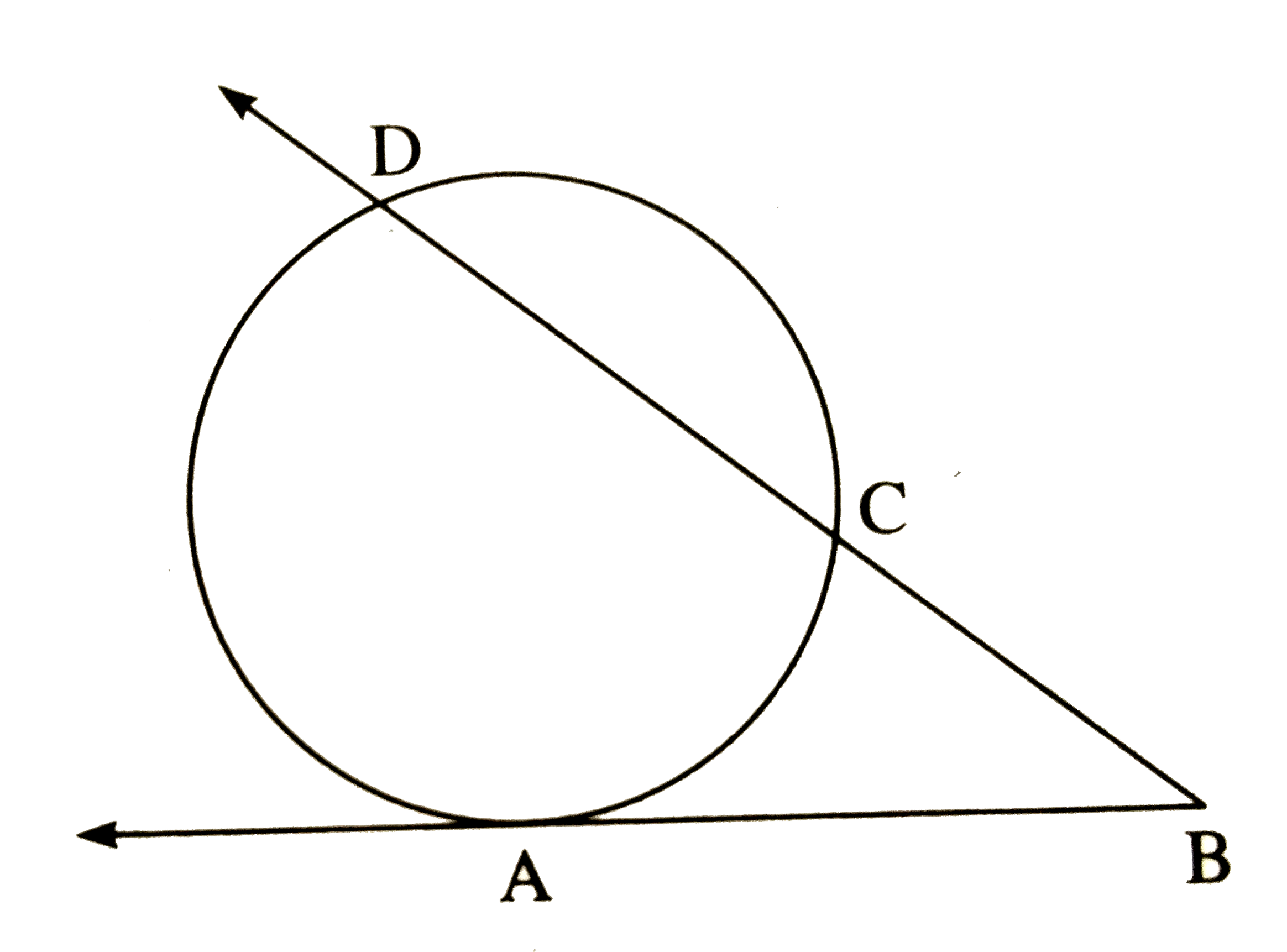
Given : Line ET is tangent to the circle at point E. Line EAB is secant intersecting at point A and B.
To Prove :ET2=EA×EB
Construction : Draw seg BT and Seg AT
Complete the proof by filling the boxes.

In ΔEAT and ΔETB,
∠AET≅∠TEB ….□
∠ETA≅∠EBT ….□
∴ΔEAT~ΔETB …□
∴ET□=EA□ ….(Corresponding sides of similar triangle )
∴EA×EB=□
Proof :
In ΔEAT and ΔETB.
∠AET≅TEB ....Common angle
∠ETA≅∠EBT .....Tangent secant theorem
∴ΔEAT~ΔETB ....A A test of similarity
∴ETEB=EAET ....(Corresponding sides of similar triangle )
∴EA×EB=ET2
Topper's Solved these Questions
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:4.5 (1 mark each)
Explore 7 Videos
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:ASSIGNMENT 4.1
Explore 10 Videos
- CIRCLEBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CIRCLEExercise:4.3 (1 mark each)
Explore 11 Videos
- CHALLENGING QUESTIONSBook:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:CHALLENGING QUESTIONSExercise:SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
Explore 1 Video
- COORDINATE GEOMETRY Book:NAVNEET PUBLICATION - MAHARASHTRA BOARDChapter:COORDINATE GEOMETRY Exercise:Assignment 6.5
Explore 13 Videos
Similar Questions
Knowledge Check
Equation of the tangent to the circle at the point (1, -1) whose centre is the point of intersection of the straight lines x-y=1 and 2x+y-3=0, is
A3x-y-4=0Bx+4y+3=0Cx-3y-4=0D4x+y-3=0
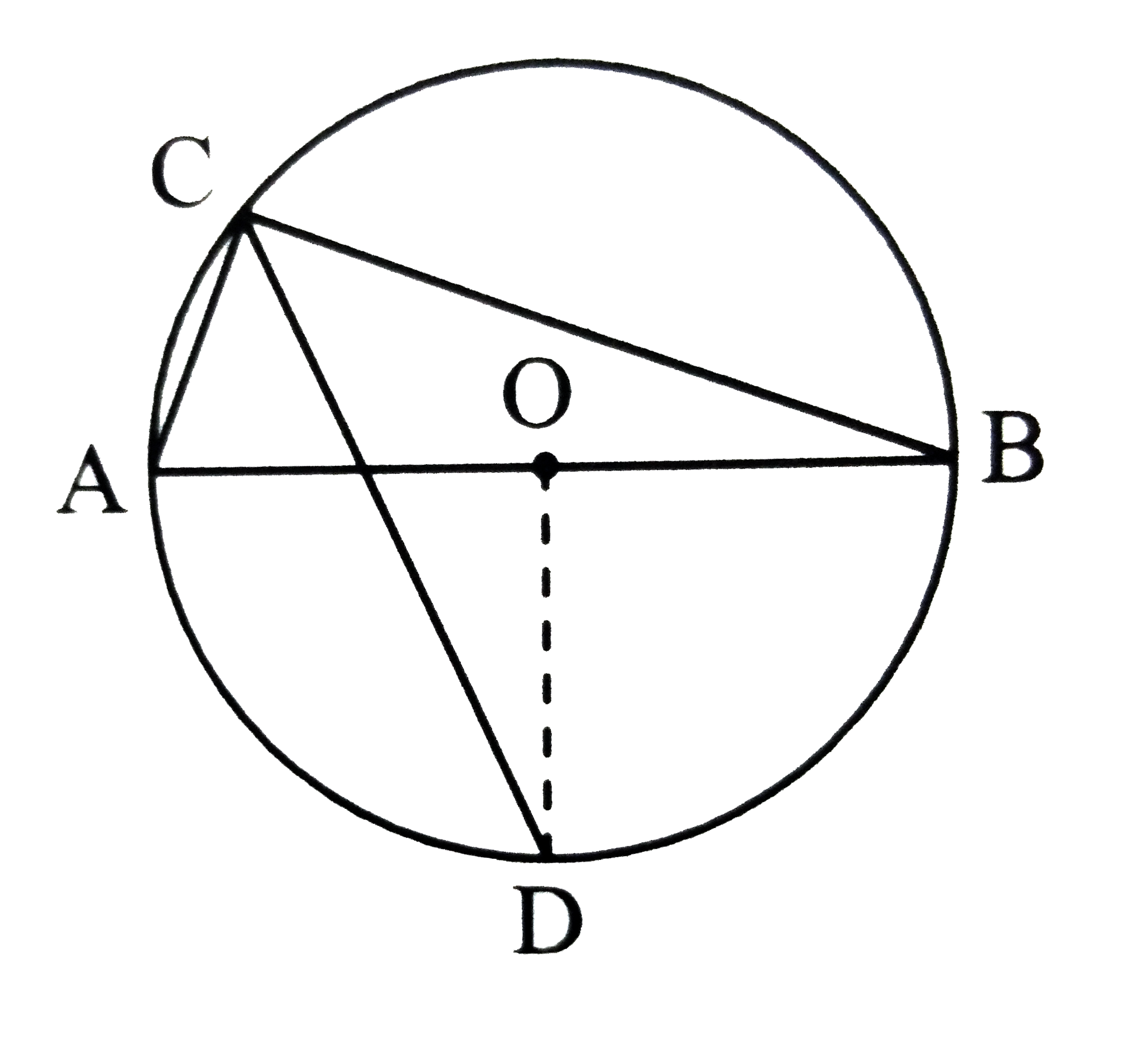
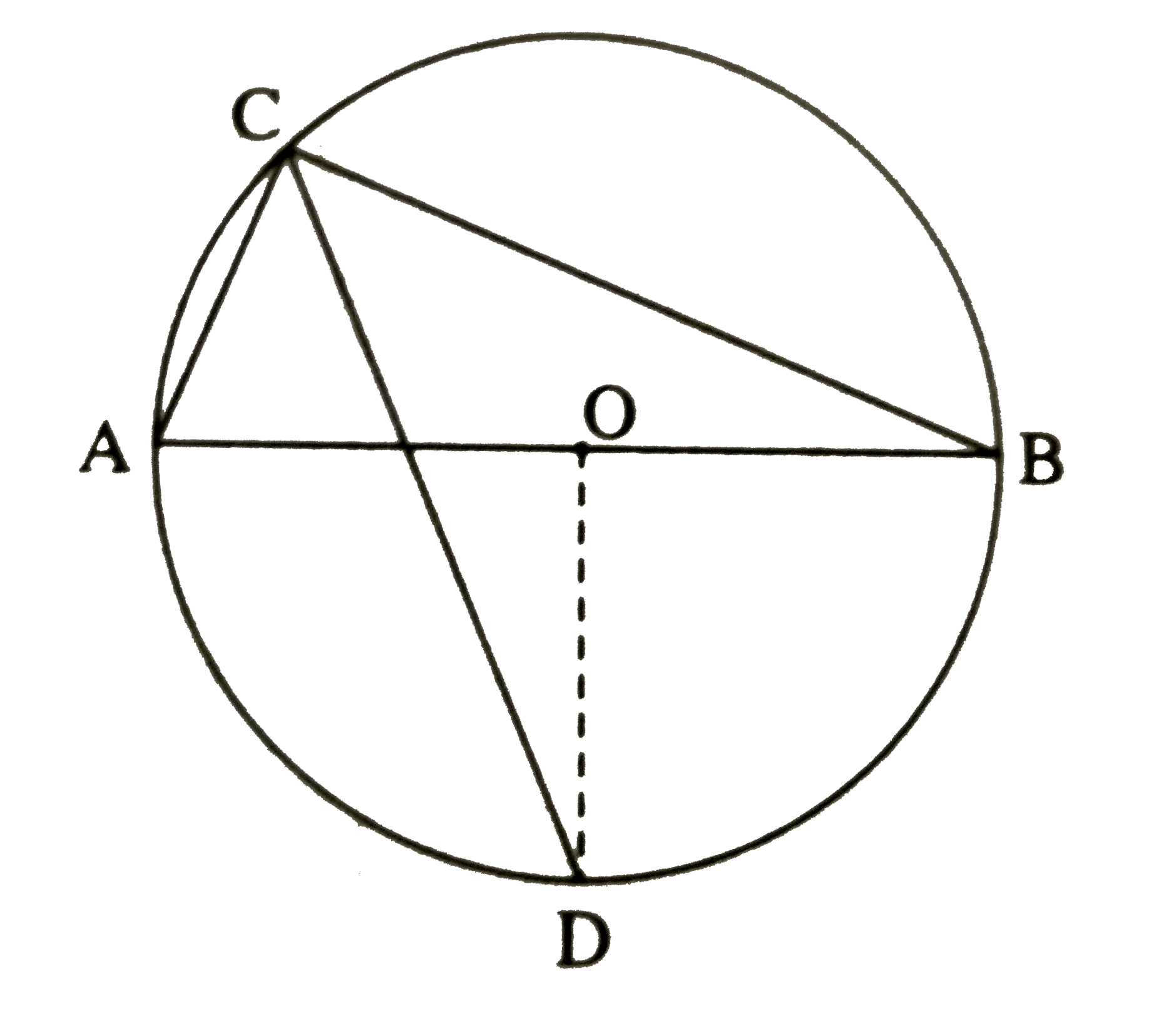
In the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
View SolutionTheorem of external division of chords.
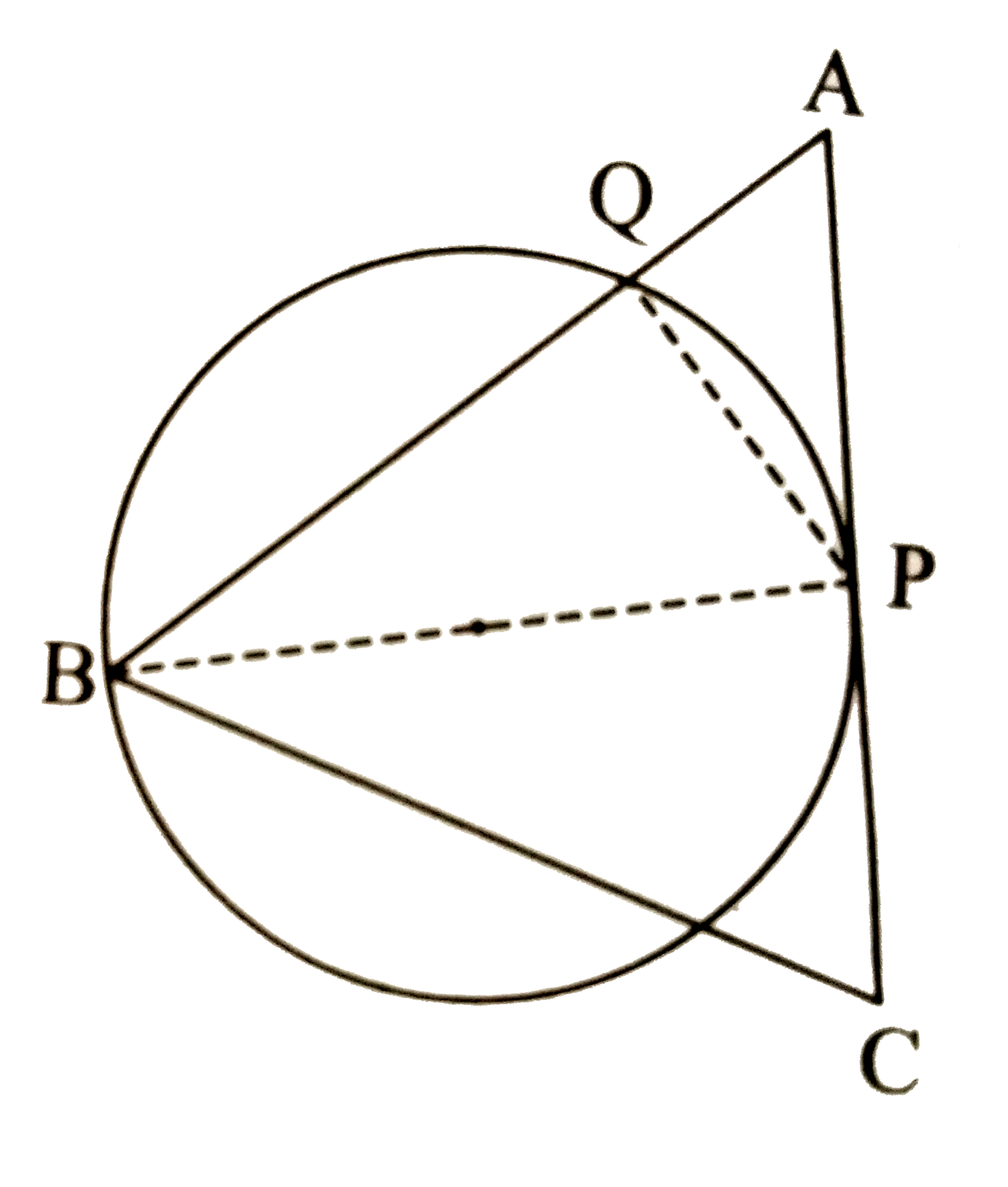
If secants containing chords AB and CD of a circle intersect outside the circle in point E, then AE×EB=CE×ED
Given : (1) A circle with centre O
(2) Secants AB and CD intersect at point E outside the circle.
To prove : AE×EB=CE×DE
Construction : Draw seg AD and seg BC
View SolutionIn figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that seg AD ≅ seg BD. Complete the following proof by filling in the blanks
View SolutionTheorem of internal division of chords.
Suppose two chords of a circle intersect each other in the interior of the circle, then the product of the lengths of the two segments of one chord is equal to the product of the lengths of the two segments of the other chord.
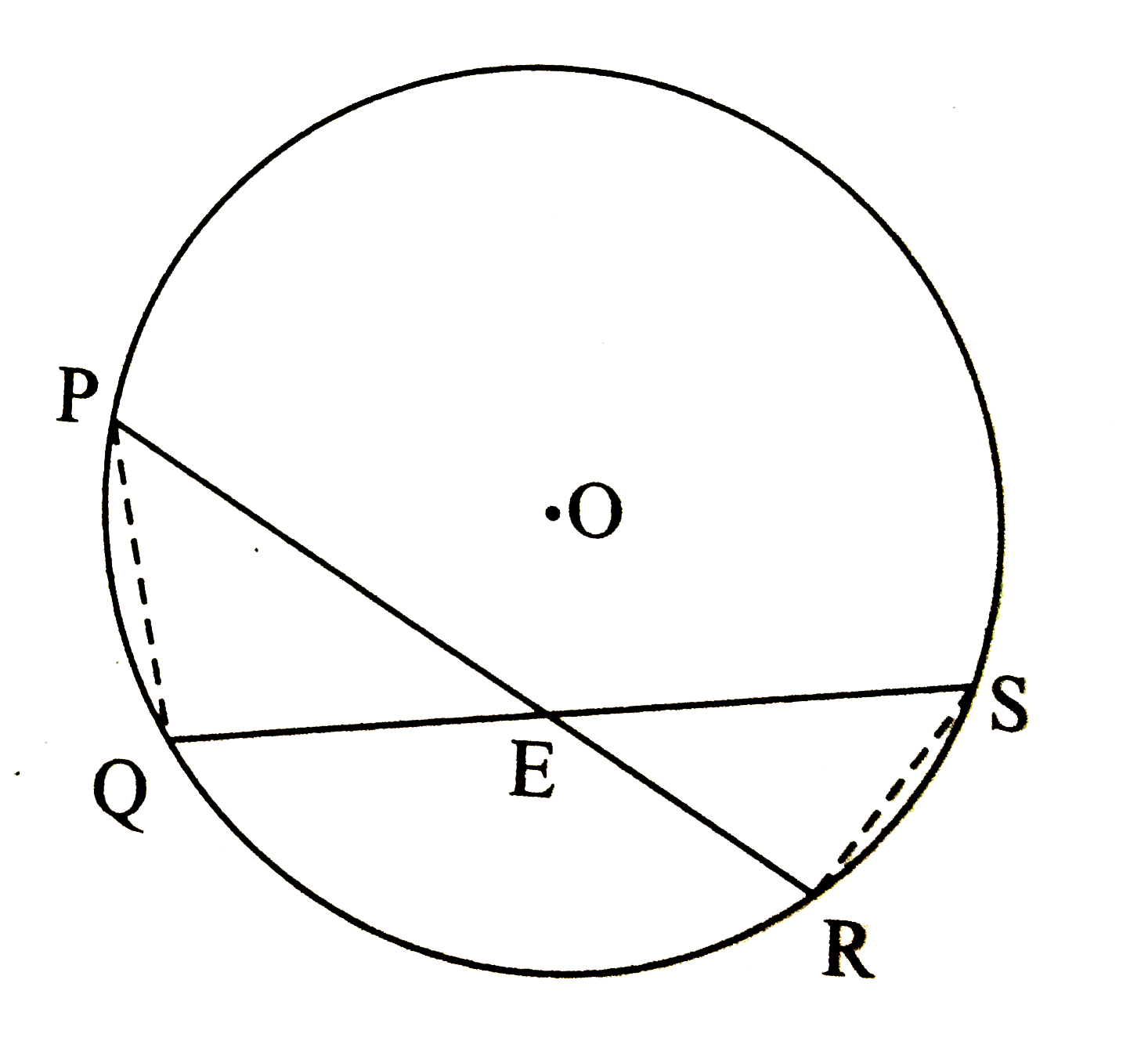
Given : (1) A circle with centre O .
(2) chords PR and QS intersect at point E inside the circle.
To prove : PE × ER = QE xx ES <br>Construction: Draw seg PQ and seg RS
View Solution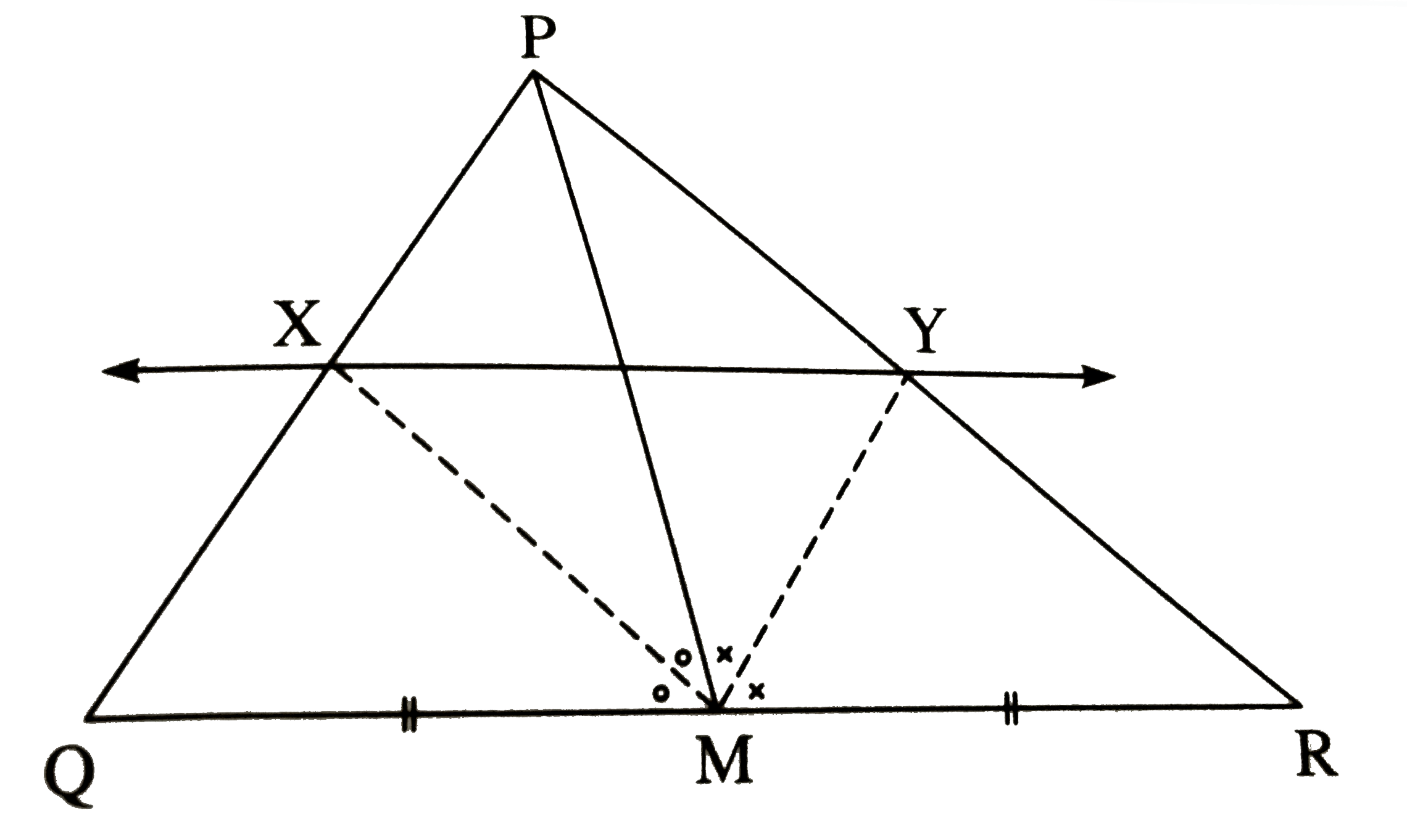
In ΔPQR seg PM is a median. Angle bisectors of ∠PMQ and ∠PMR interesect side PQ and side PR in points X and Y respectively. Prove that XY∣∣QR.
Complete the proof byfilling in the boxes:
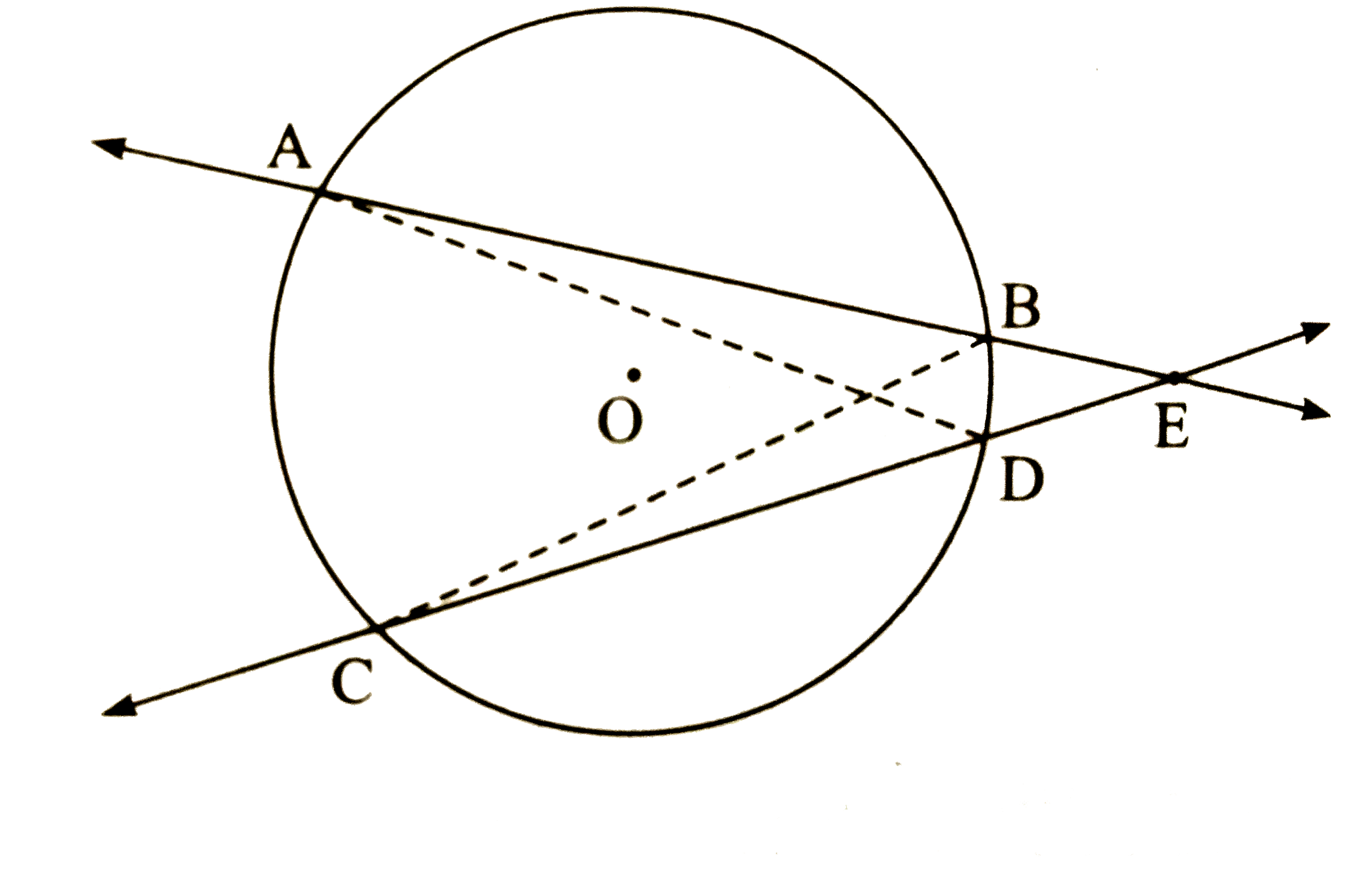
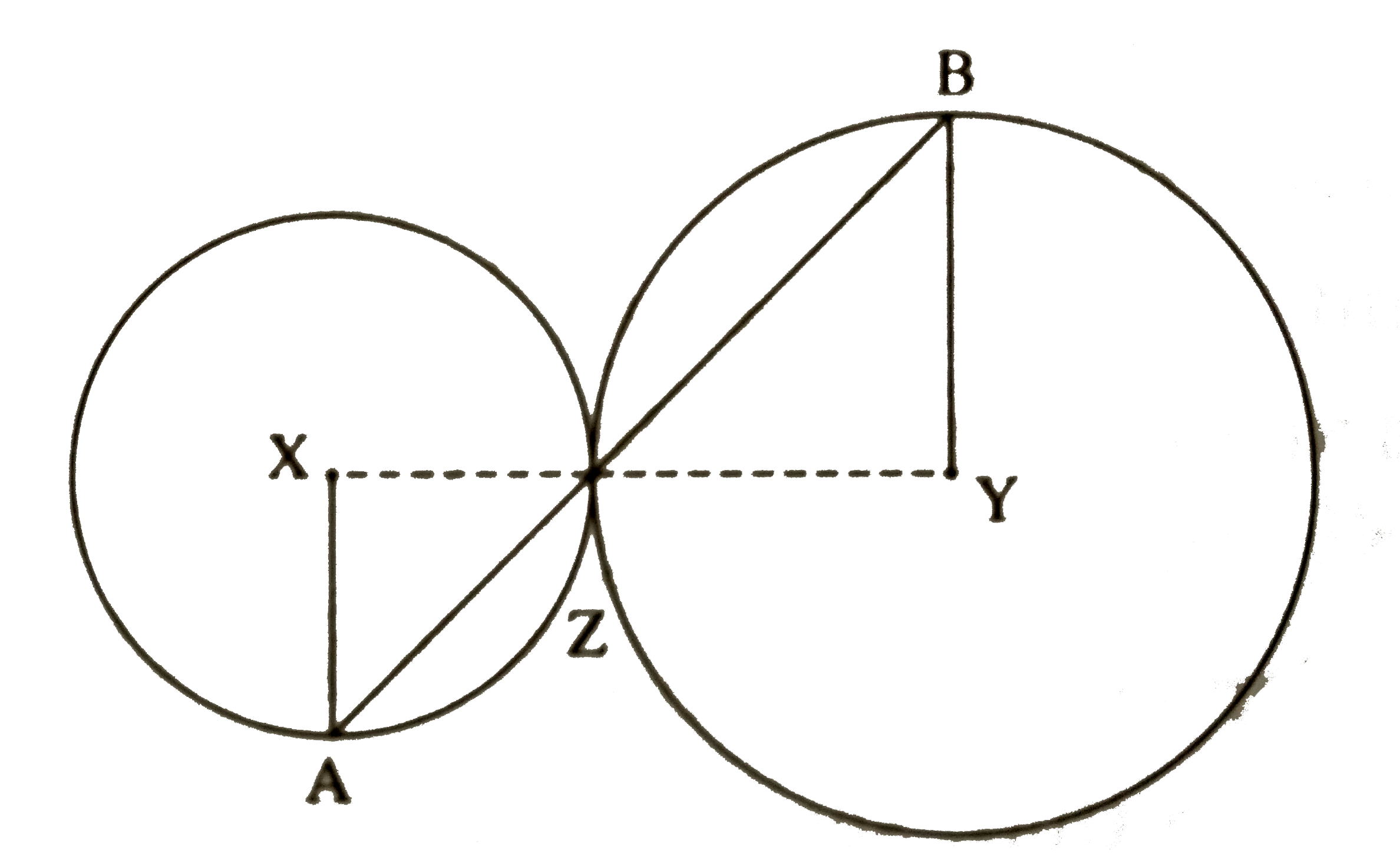
View SolutionIn the figure, circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, raduis XA || radius YB. Fill in the blanks and complete the proof:
View SolutionTheorem of angle between tangent and secant
If an angle has its vertex on the circle, its one side touches the circle and the other intersects the circle in one more point, then the measure of the angle is half the measure of its intercepted arc .
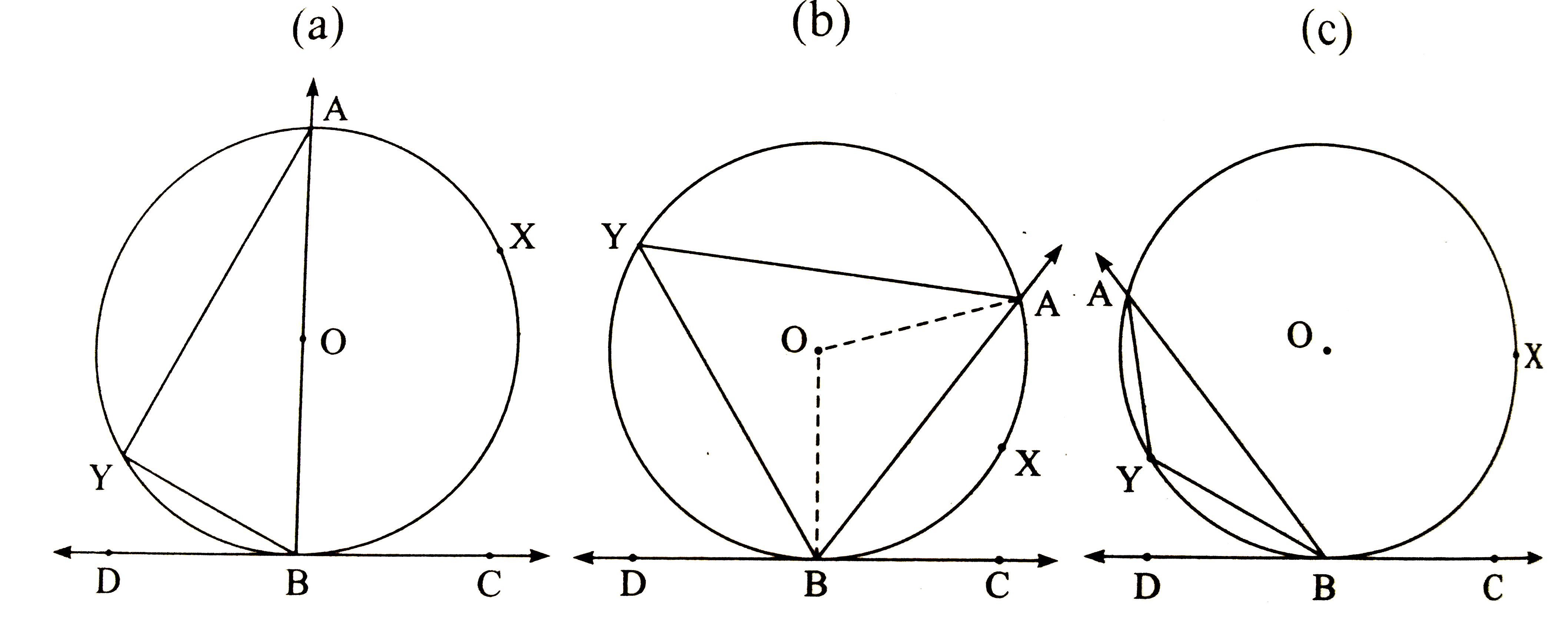
Given : Let O be the centre of the circle. Line DBC is tangent to the circle at point B. Seg BA is a chord of the circle. Point X of the circle is on C side of line BA and point Y of the circle is on D side of line BA.
To prove : m ∠ABC=12m(arcAXB).
View Solution