In the figure , ΔQRS is an equilateral triangle.
Prove that
(1) arc RS ≅arcQS≅ arc QR
(2) m (arc QRS ) =240∘.
Proof :
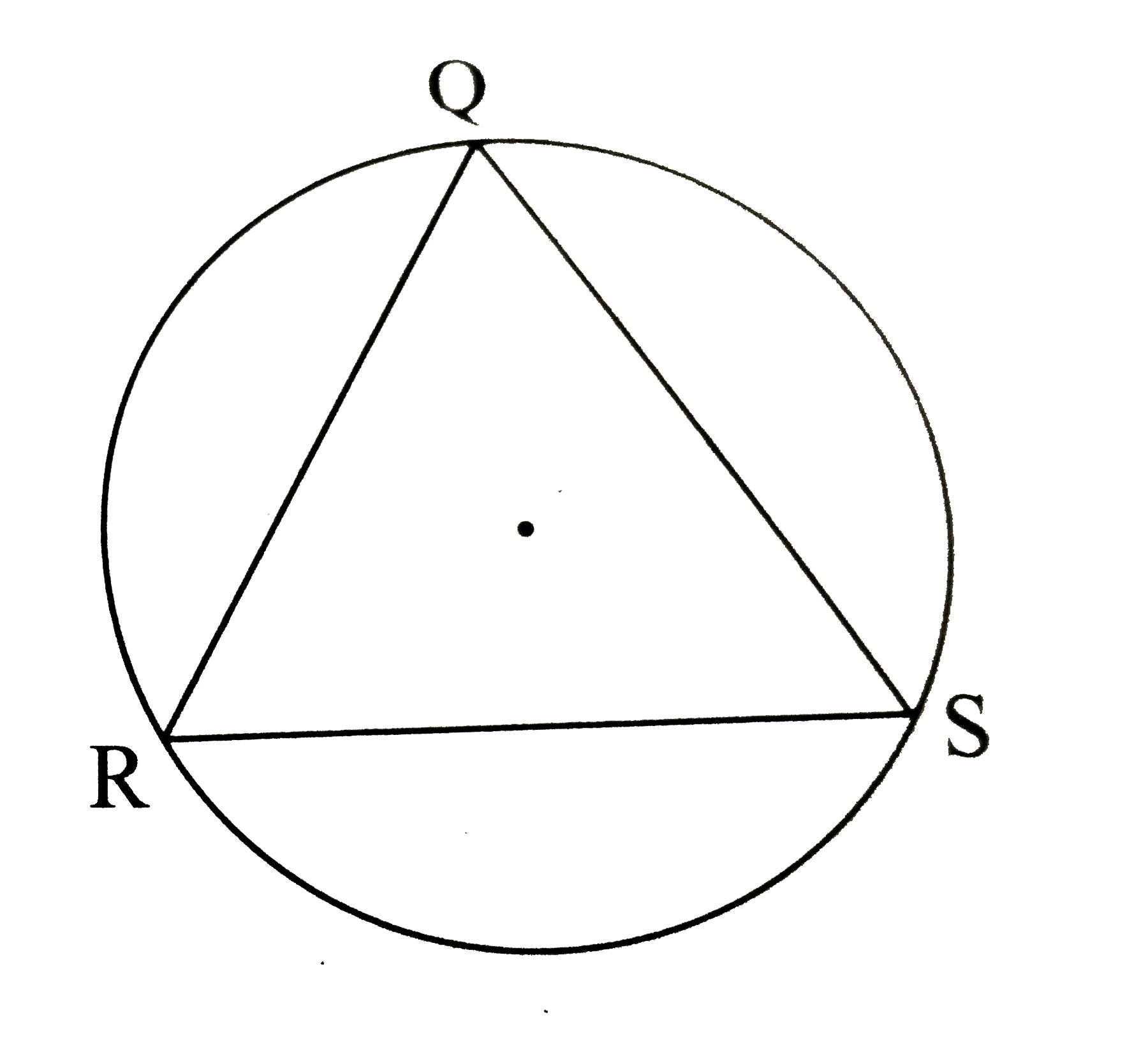
ΔQRS is an equilateral triangle ….(Given )
∴ seg RS ≅ seg QS ≅ seg QR …(Sides of equilateral triangle )
Arcs of the same circle are equal, if the related chords are congruent.
∴ arc RS ≅ arc QS ≅ arc QR ....(1)
Let m(arc RS ) = m (arc QS ) = m (arc QR ) = x
m ( arc RS ) + m (arc QS ) + m ( arc QR ) =360∘ ....( Measure of the circle is 360∘ )
∴x+x+x=360∘ ....[From (1) ]
∴3x=360∘
∴x=3603
∴x=120∘
∴ m ( arc RS ) = m (arc QS ) = m (arc QR )=120∘
m(arc QRS ) = m (arc ( QR 0 + m (arc RS ) ....(Arc addition postulate )
∴ m ( arc QRS ) =120∘+120∘
∴ m ( arc QRS ) = 240∘
Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.5 (1 mark each)
7 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.1
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.3 (1 mark each)
11 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
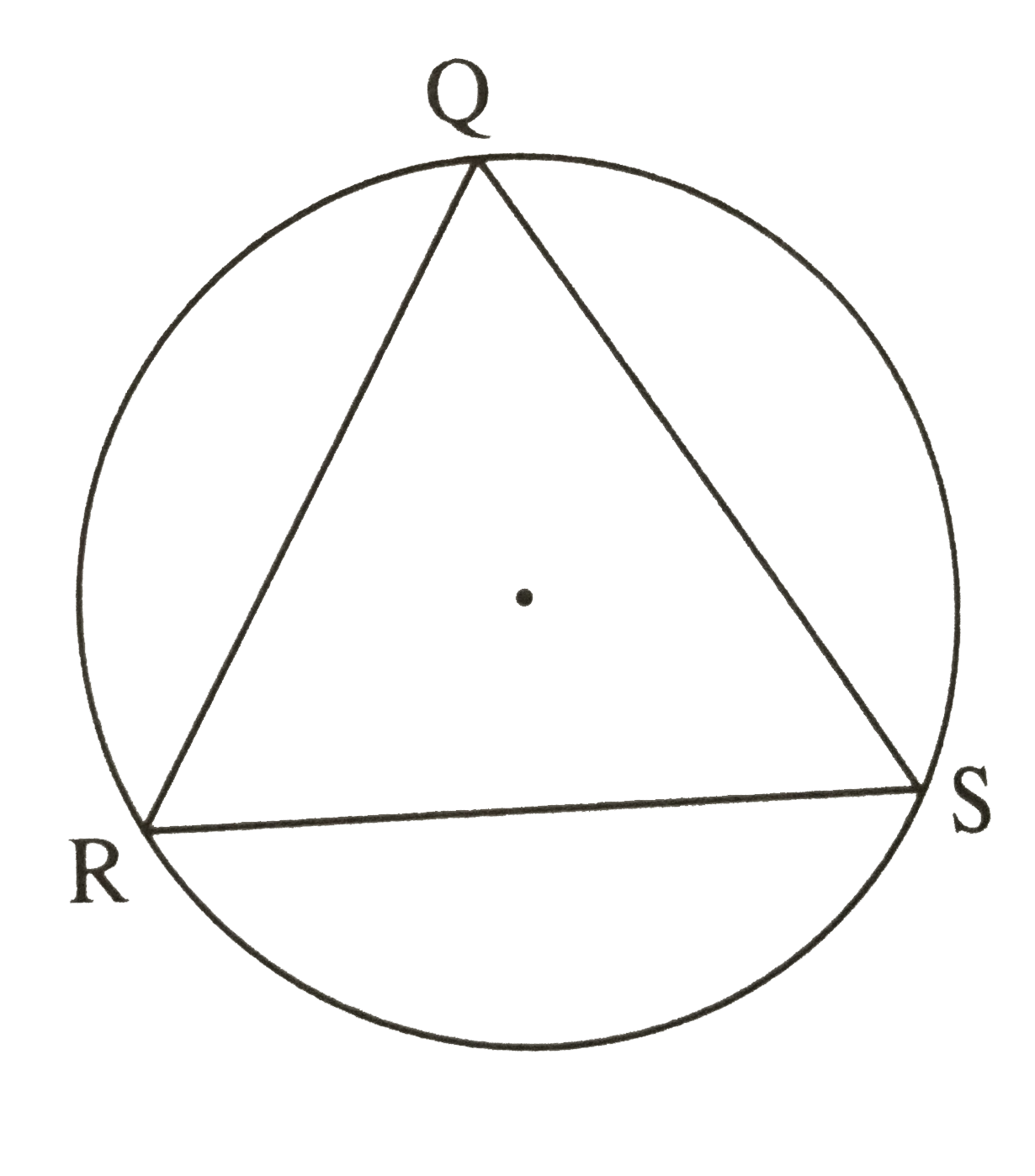
In figure, △QRS is an equilateral triangles. Prove that,
(1) arcRS≅arcQS≅arcQR
(2) m(arcQRS)=240∘.
View SolutionIn the figure ΔPQR is an equilateral triangle. Point S is on seg QR such that
QS=13QR.
Prove that : 9PS2=7PQ2

View SolutionIn the figure 2.35,ΔPQR is an equilatral triangle. Point S is on seg QR such that QS=13QR. Prove that : 9PS2=7PQ2
View SolutionIn the given figure, I Rs = 3√3 cm and RPS is an equilateral triangle, then find the value of QR
View SolutionIn the adjoining figure, ΔPQR is an equilateral triangle. Point S is on seg QR. such that QS=13QR. Prove that : 9PS2=7PQ2.
View Solution1. In the figure △PQR is an equilateral triangle, the point N is on ray QR such that QR=RN. Prove that PN2=3PR2
View SolutionIn the figure , ∠QPR has its vertex outside the circle such that m ( arc QR ) = 200∘ and m ( arc ST ) =90∘, then ∠QPR= ?

View SolutionIn the given figure, ABC is an equilateral triangle; PQ∣∣AC and AC is produced to R such that CR=BP. Prove that QR bisects PC
View SolutionIn the givne figure, ABC is an equilateral triangle, PQ||AC and AC is produced to R such that CR = BP. Prove that QR bisects PC.
View SolutionIn the given figure, name the following:

an arc
View Solution
