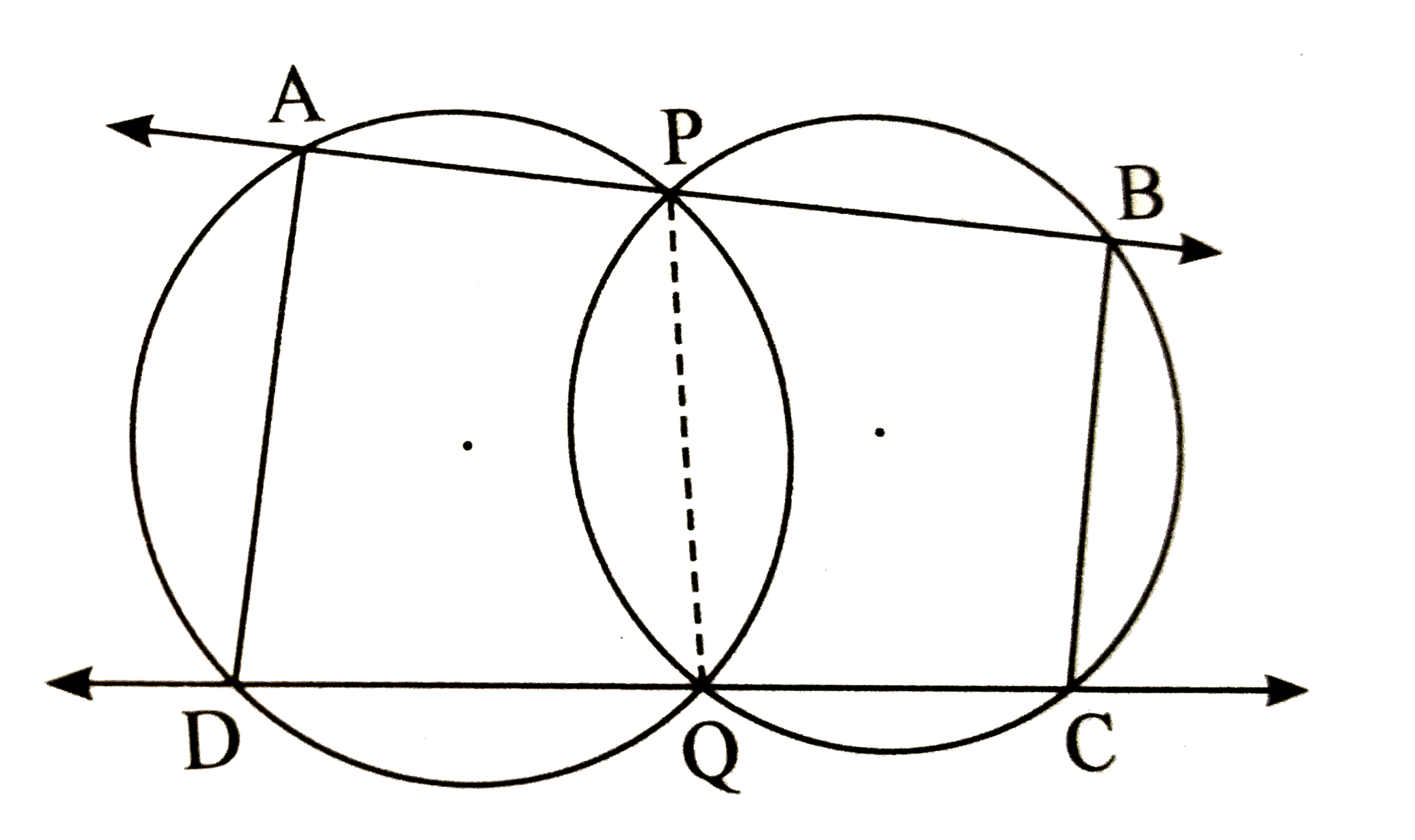
In the figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ ∣∣ seg RP.

Draw seg MN
□ MRPN is cyclic and ∠MNQ is its exterior angle.
∠MNQ=∠MRP ….(1) …...(Corollary of cyclic quadrilateral theorem )
□ MNQS is cyclic
∴∠MNQ+∠MSQ=180∘0 …(Theorem of cyclic quadrilateral )
∴∠MRP+∠MSQ=180∘ ....[From (1) ]
∴∠SRP+∠RSQ=180∘ .....(R-M-S)
∴ seg SQ∣∣ seg RP ....(interior angles test for parallel lines )
Topper's Solved these Questions
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.5 (1 mark each)
7 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - ASSIGNMENT 4.1
10 Videos
- CIRCLEBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - 4.3 (1 mark each)
11 Videos
- CHALLENGING QUESTIONSBOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :
1 Videos
- COORDINATE GEOMETRY BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.5
13 Videos
Similar Questions
In figure, two circles intersect at points M and N. Secants drawn through M and N intersect the circles at points R,S and P,Q respectively. Prove that : seg SQ || seg RP.

View SolutionTwo circles intersect each other at point P and Q. Secants drawn through p and Q intersect the circles at points A,B and D,C
Prove that :∠ADC+∠BCD=180∘
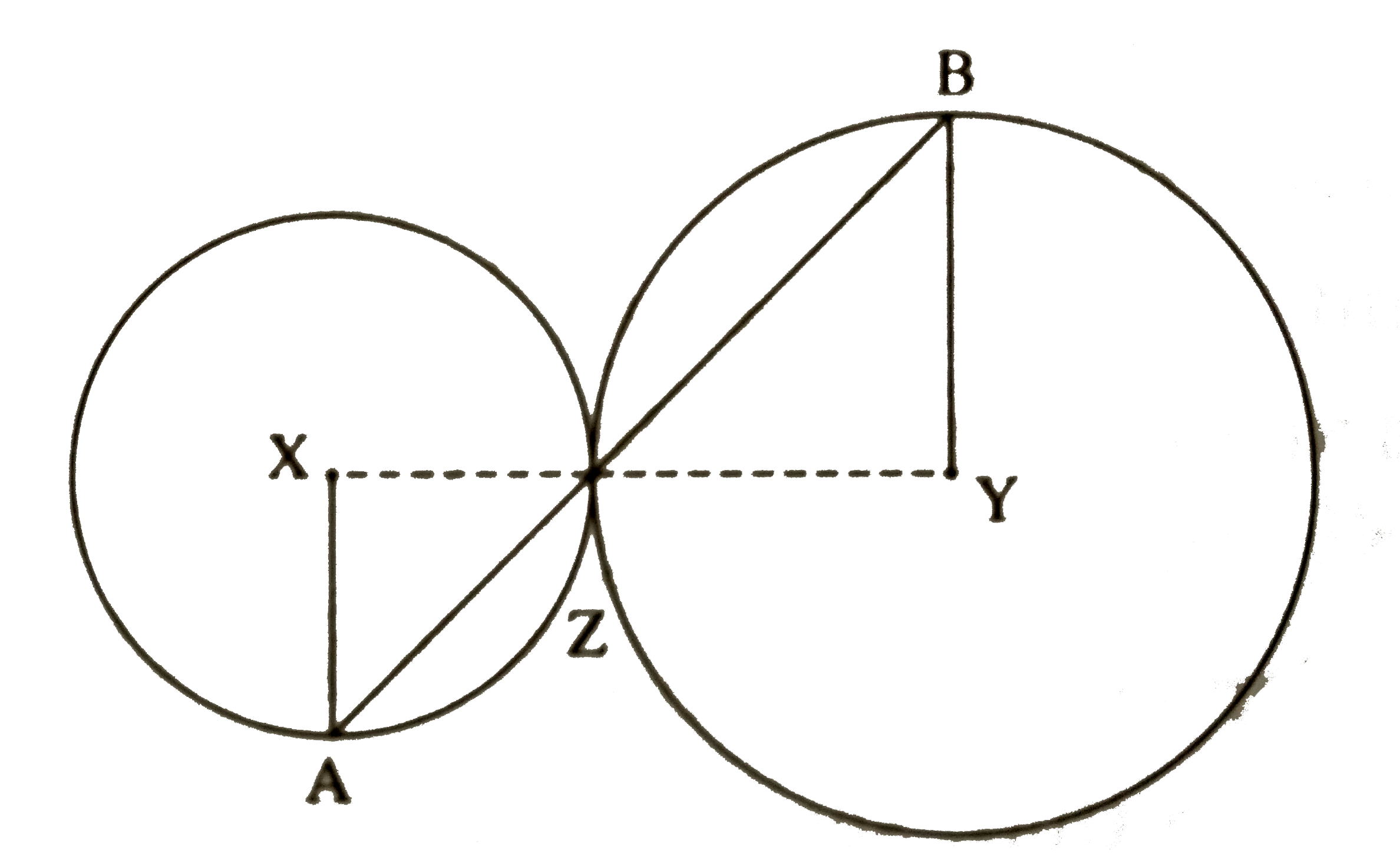
View SolutionIn the figure, circles with centres X and Y touch each other at point Z. A secant passing through Z intersects the circles at points A and B respectively. Prove that, raduis XA || radius YB. Fill in the blanks and complete the proof:
View SolutionAs shown in the adjoining figure , two circles centred at A and B are touching at C. Line passing through C intersects the two circles at M and N respectively.
Show that seg AM ∣∣seg BN.
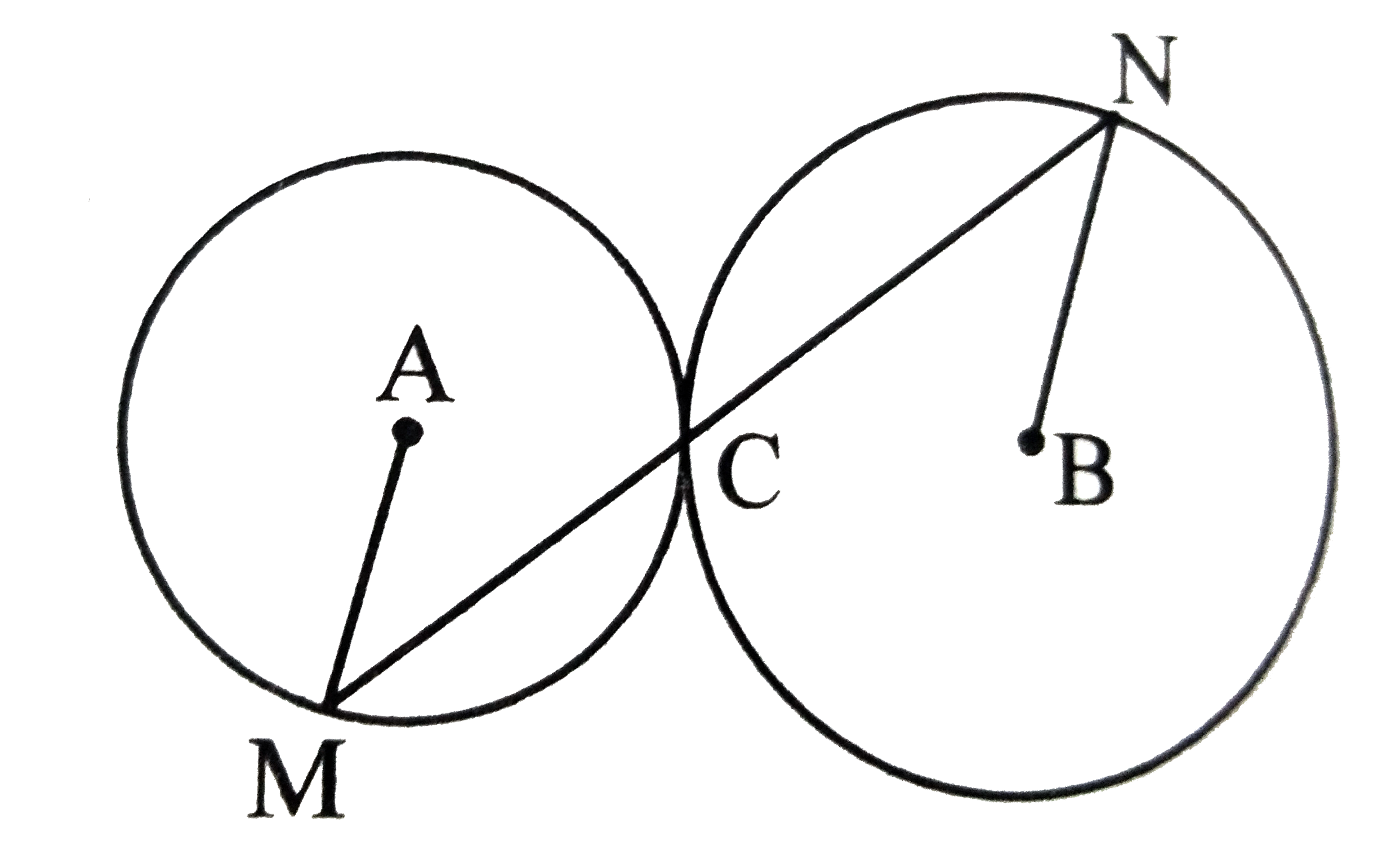
View SolutionIn the fig. two circles intersect each other in point A and B. Secants through the point A intersect the circles in point P,Q and R,S. Line PR and SQ intersect in T. (i) PTQ and PBQ are supplementary. (ii) □ BSTR is cyclic quadrilateral.
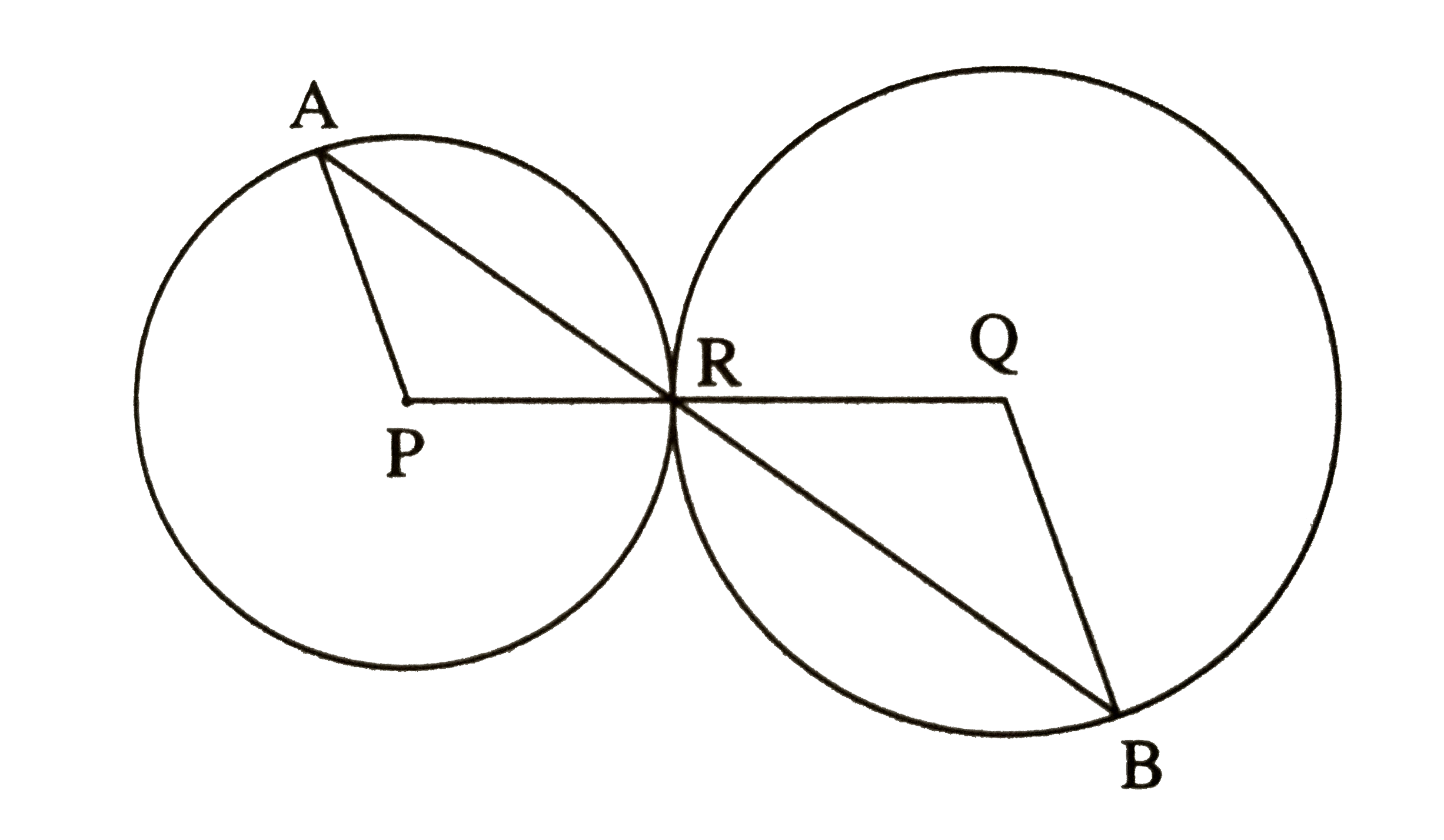
View SolutionIn the figure, the circles with centers P and Q touch each other at R.A line passing through R meets the circles at A and B respectively. Prove that
seg AP || seg BQ
View SolutionIn figure, two circles intersect each other at points A and E. Their common secant through E intersects the circles at points B and D. The tangents of the circles at points B and D intersect each other at point C. Prove that □ ABCD is cyclic.

View SolutionIn the figure, two circles intersect each other in points P and Q. If tangent from point R touch the circles at S and T, then prove that RS=RT.
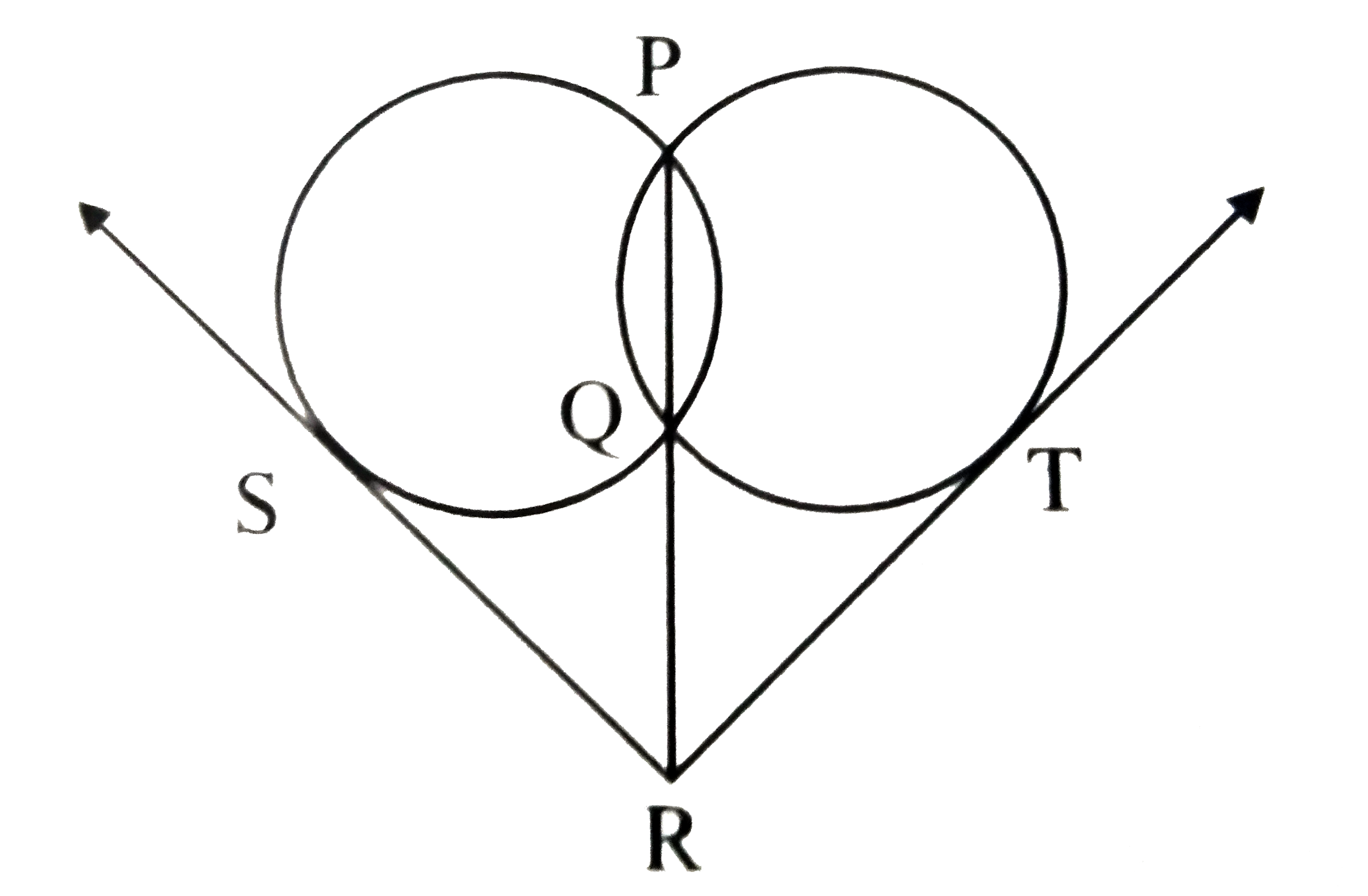
View SolutionIn figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.

View SolutionIn the given figure two circles intersect at two points B and C. Two line segments ABD and PBQ passing through point B, intersects circles respectively at A, D and P, Q . Prove that ∠ACP=∠QCD
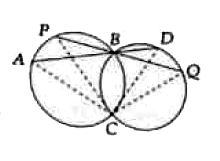
View Solution
