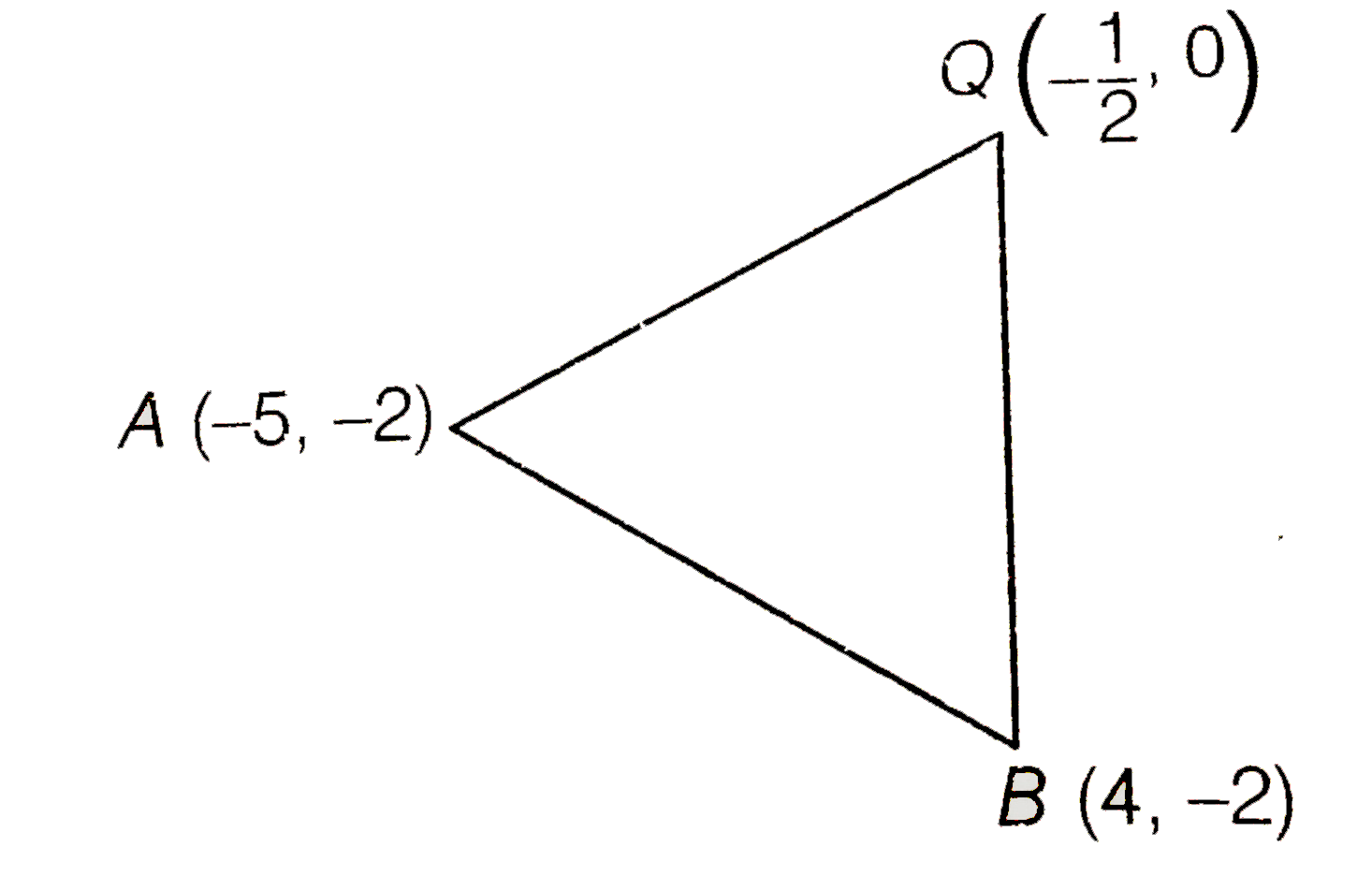
Find the coordinates of the point Q on the X- axis which lies on the perpendicular bisector of the line segment joining the points A (-5,-2) and B (4,-2). Name the type of triangle formed by the points Q , A and B.
Video Solution
Text Solution
Firstly , we plot the points of the line segment on the paper and join them.

We know that, the perpendicular bisector of the line segment AB bisect the segment AB i.e., perpendicular bisector of line segment AB passes through the mid- point of AB.
∴ Mid - point of AB(−5+42,−2−22)
⇒R=(−12,−2)
[∵ mid - point of a line segment passes through the points (x1,y1)and(x2,y2) is(x1+x22,y1+y22)]
Now , we draw a straight line on paper passes through the mid- point R. We that perpendicular bisector cuts the X-axis at the point Q (−12,0).
Hence, the required coordinates Q≡(−12,0)
Alternate Method
(i) To find the coordinates of the point of Q on the X -axis . We find the equation of perpendicular bisector of the line segment AB.
Now , slope of line segment AB,
Let m1=y2−y1x2−x1=−2−(−2)4−(−5)=−2+24+5=09
⇒m1=0
Let the slope of perpendicular bisector of line segment is m2.
since, perpendicular bisector is perpendicular to the line segment AB.
By perpendicularity condition of two lines,
m1⋅m2=−1
⇒m2=−1m1=−10
⇒m2=∞
Also , we know that , the perpendicular bisector is always passes through the mid- point of the line segment.
∴ Mid - point (−5+42,−2−22)=(−12,−2)
[∵ mid - point =(x1+x22,y1+y22)]
To find equation of perpendicular bisector of line segment , we find the slope and a point through which perpendicular bisector is pass.
Now , equation of perpendicular bisector having slope ∞ and passing through the point (−12,−2) is
(y+2)=∞(x+12) " " [∵(y−y1)=m2(x−x1)]
⇒y+1x+12=∞=10⇒x+12=0
∴x=−12
So , the coordinates of the point Q is (−12,0) on the X -axis which lies on the perpendicular bisector of the line segment joining the point AB.
to know the type of triangle formed by the point Q , A and B , We find the length of all three sides and see whatever condition of triangle is satisfy by these sides .
Now , using distance formed between two points,
AB=√(4+5)2+(−2+2)2=√(9)2+0=9
[∵ distance between two points (x1,y1)and(x2,y2)=√(x2−x1)+(y2−y1)2] BQ =√(−12−4)2+(0+2)2
=√(−92)2+(2)2=√814+4=√974=√972
and QA =√(−5+12)+(−2−0)2
=√(−92)2+(2)2
=√814+4=√974=√972
We see that , BQ=QA≠AB
which shows that the triangle formed by the points Q ,A and B is an isosceles.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions7videos
CONSTRUCTIONS
- BOOK - NCERT EXEMPLARCHAPTER - INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONSEXERCISE - Introduction To Trigonometry And Its Applications60videos
INTRODUCTION TO TRIGoNOMETRY AND ITS APPLICATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
The point which lies on the perpendicular bisector of the line segment joining the points A(-2,-5) and B (2,5) is
A(0,0)B(0,2)C(2,0)D(-2,0) - Question 2 - Select One
The point which lies on the perpendicular bisector of the line sequent joining the points P(−2,0) and Q(2,5) is
A(0,0)B(0,2)C(2,0)D(−2,0) - Question 3 - Select One
The perpendicular bisector of the line segment joining the points A(1,5) and B(4,6) cuts the Y-axis at
A(0,13)B(0,-13)C(0,12)D(13,0)
Find the equation of the perpendicular bisector of the line segment joining the points A(2,3)andB(6,−5).
View SolutionFind the equation of the perpendicular bisector of the line segment joining the points A(2,3) and B(6,−5).
View SolutionThe equation of the perpendicular bisector of line segment joining points A(4,5) and B(-2,3) is
View SolutionThe perpendicular bisector of the line segment joining the points A(1,5)andB(4,6) cuts the y-axis at which point?
View SolutionThe equation of the perpendicular bisector of line segment joining points A (4,5) and B (−2,3) is :
View Solution
