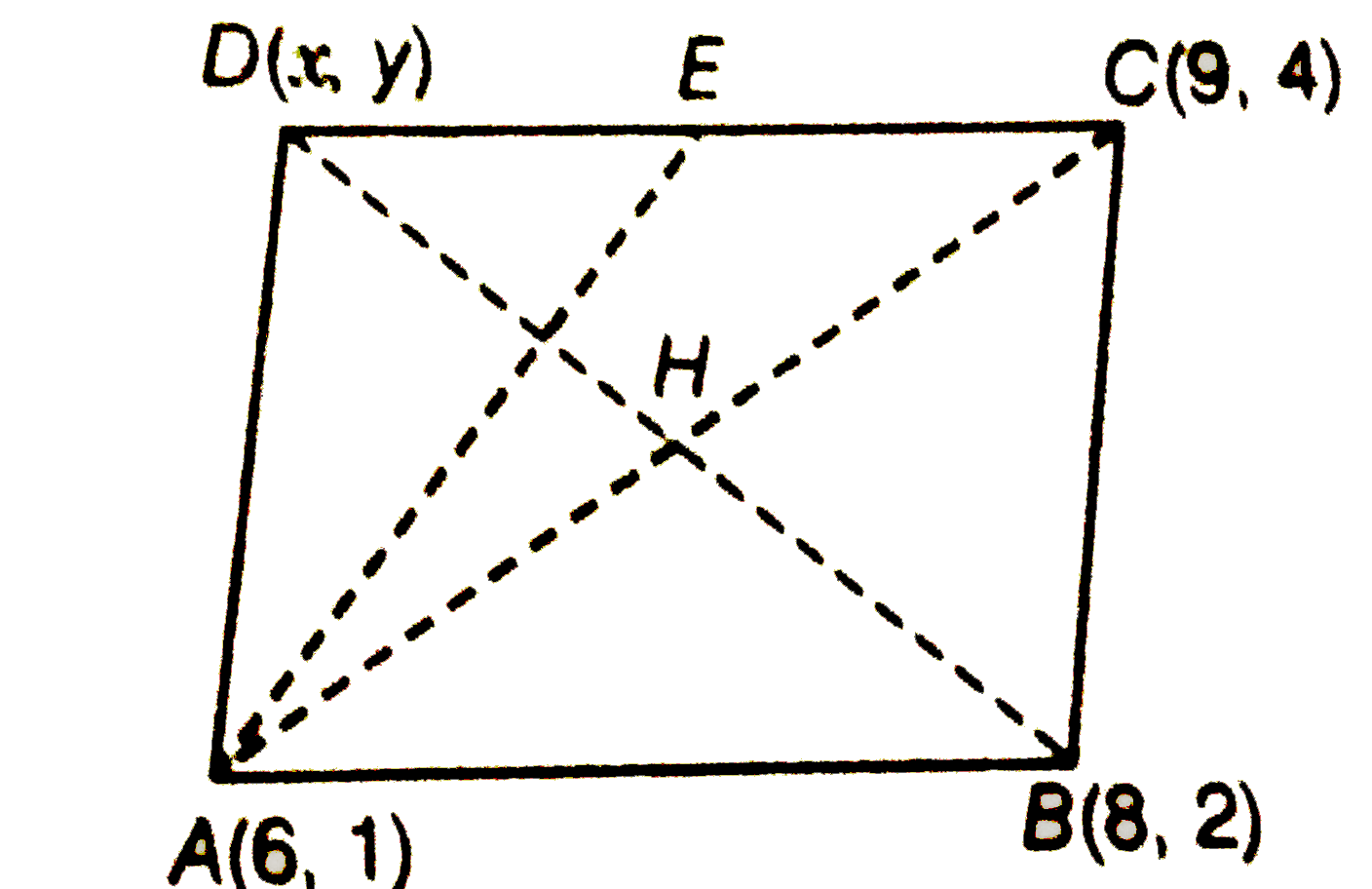
A(6,1) , B (8,2) and C (9,4) are three vertices of a parallelogram ABCD . If E is the mid - point of DC , then find the area of $△$ ADE.

Video Solution

Text Solution

Verified by Experts

A(6,1) , B (8,2) and C (9,4) are three vertices of a parallelogram ABCD . Let the fourth vertex of paralleogram be (x,y). We know that. The ,the diagonals os a parallelogram bisect each other.

$∴$ Mid - point of BD = Mid point of AC
$\Rightarrow (\frac{8 + x}{2}, \frac{2 + y}{2}) = (\frac{6 + 9}{2}, \frac{1 + 4}{2})$
[ $∵$ mid - point of a line segment joining the points $(x_{1}, y_{1}) and (x_{2}, y_{2}) = (\frac{x_{1} + x_{2}}{2}, \frac{y_{1} + y_{2}}{2})]$
$\Rightarrow (\frac{8 + x}{2}, \frac{2 + y}{2}) = (\frac{15}{2}, \frac{5}{2})$
$∴ \frac{8 + x}{2} = \frac{15}{2}$
$\Rightarrow 8 + x = 15 \Rightarrow x = 7$
and $\frac{2 + y}{2} = \frac{5}{2}$
$\Rightarrow 2 + y = 5 \Rightarrow y = 3$
So ,fourth vertex of a parallelogram is D (7,3).
Now , mid - point of side DC $\equiv (\frac{7 + 9}{2}, \frac{3 + 4}{2})$
E $\equiv (8, \frac{7}{2})$
[ $∵$ area of $△$ ABC with vertices $(x_{1}, y_{1}), (x_{2}, y_{2}) and (x_{3}, y_{3}) = \frac{1}{2} [x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + (y_{1} - y_{2})]$
$∴$ Area of $△$ ADE with vertices A (6,1),D (7,3) and $(8, \frac{7}{2})$ ,
$△ = \frac{1}{2} [6 (3 - \frac{7}{2}) + 7 (\frac{7}{2} - 1) + 8 (1 - 3)]$
$= \frac{1}{2} [6 \times (\frac{- 1}{2}) + 7 (\frac{5}{2}) + 8 (- 2)]$
$= \frac{1}{2} (3 + \frac{35}{2} - 16)$
$= \frac{1}{2} (\frac{35}{2} - 19) = (\frac{- 3}{2})$
$= \frac{- 3}{4}$ [but area cannot be negative]
Hence , the required area of $△$ ADE is $\frac{3}{4}$ sq units.

Updated on:21/07/2023

The points $A (4, 5, 10), B (2, 3, 4) and C (1, 2, - 1)$ are three vertices of a parallelogram ABCD, then
AVector equation of AB is $2 i + 3 j + 4 k + λ (i + j + 3 k)$
BCartesian equation of BC is $\frac{x - 2}{1} = \frac{y - 3}{1} = \frac{z - 4}{- 5}$
CCoordinate of D are $(3, 4, 5)$
DABCD is a rectangle.