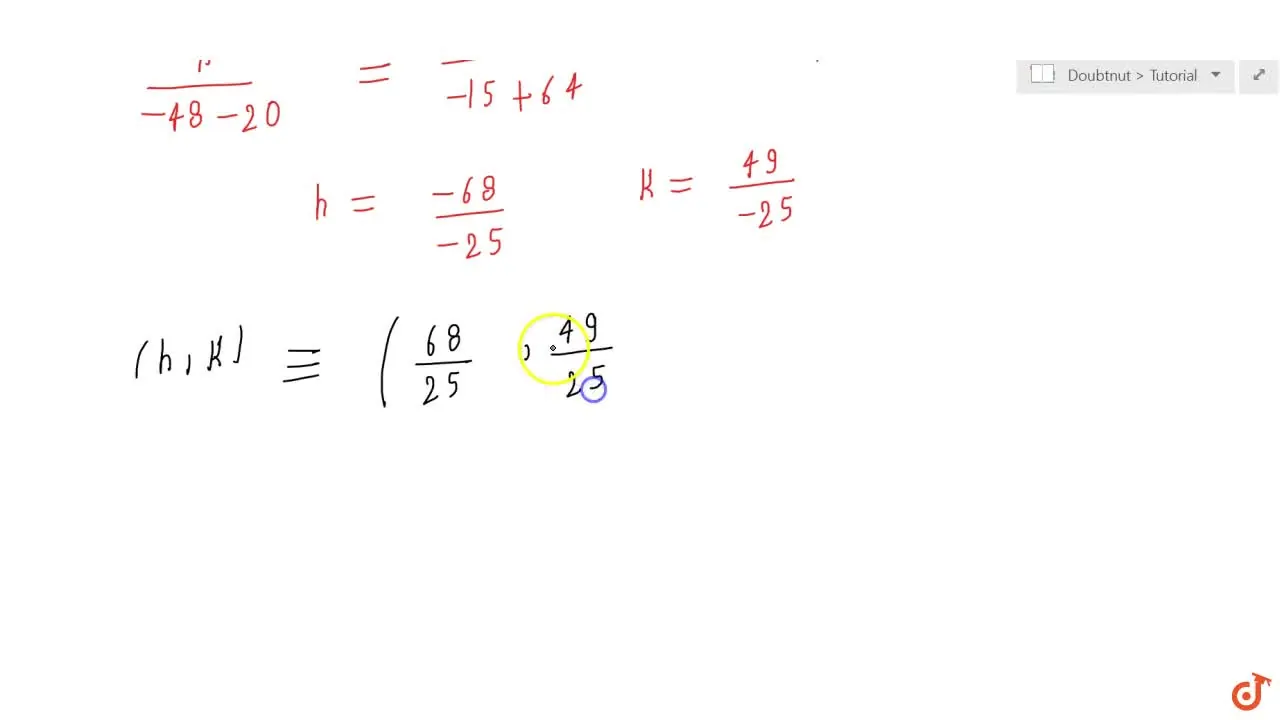Find the coordinates of the foot of perpendicular from the point (1,3)to the line 3x4y16=0.
Given line is 3x−4y−16=0→(1)
We will bring it in general form, y=mx+c
4y=3x−16
y=34x−4
So, slope of given line, m1=34.
Now, if slope of perpendicular to this line is m2. then,
m1⋅m2=−1
m2⋅34=−1
m2=−43
Now, equation of this line at point (-1,3),
(y−3)=−43(x+1)
⇒3y−9=−4x−4
⇒4x+3y−5=0→(2)
Now, we will solve equation (1) and equation (2) to find the point of intersection.
Multiplying (1) with 3, and multiplying (2) with 4 and then adding them,
9x−12y−48+16x+12y−20=0
⇒25x=68⇒x=6825
Putting value of x in (1),
3(6825)−4y=16
⇒20425−4y=16⇒100y=−196⇒y=−4925
So, coordinates of foot of perpendicular will be (6825,−4925).
Related Playlists
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - MISCELLANEOUS EXERCISE24videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE 10.114videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STRAIGHT LINESEXERCISE - SOLVED EXAMPLES28videos
STRAIGHT LINES
- BOOK - NCERTCHAPTER - STATISTICSEXERCISE - EXERCISE 15.210videos
STATISTICS
- BOOK - NCERTCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - EXERCISE 3.17videos
TRIGONOMETRIC FUNCTIONS
Similar Questions
Find the coordinates of the foot o the perpendicular from the point (-1, 3) to the line 3x−4y−16=0
View SolutionFind the coordinates of the foot of perpendicular from a point (−1,3) to the line 3x−4y−16=0
View SolutionFind the coordinates of the foot of the perpendicular from the point (−1,3) to the line 3x−4y−16=0.
View SolutionWhat are the coordinates of the foot of the perpendicular from the point (2 , 3) on the line x + y - 11 = 0 ?
View SolutionFind the co-ordinates of the foot of perpendicular drawn from the point (3,−3) to the line x−2y=4.
View SolutionFind the coordinates of the foot of the perpendicular drawn from the point (2,3) to the line y=3x+4
View Solution(i) Find the co-ordinates of the foot of perpendicular from point (−1,3) to the line 3x−4y=16.
(ii) The co-ordinates of the foot of perpendicular drawn from origin to a line are (2,3). Find the equation of the line.View SolutionThe foot of the perpendicular from the point (3, 4) on the line 3x - 4y + 5 = 0 is
View SolutionThe foot of the perpendicular from the point (3, 4) on the line 3x - 4y + 5 = 0 is
View SolutionFind the coordinates of the foot of perpendicular from the point (2,6,3) to the line x2=y−12=z−23. Also find the equation of this perpendicular.
View Solution