Find the area enclosed by the curves x2=y,y=x+2,andx−aξs.
Video Solution
Text Solution
The correct Answer is:56 sq. units
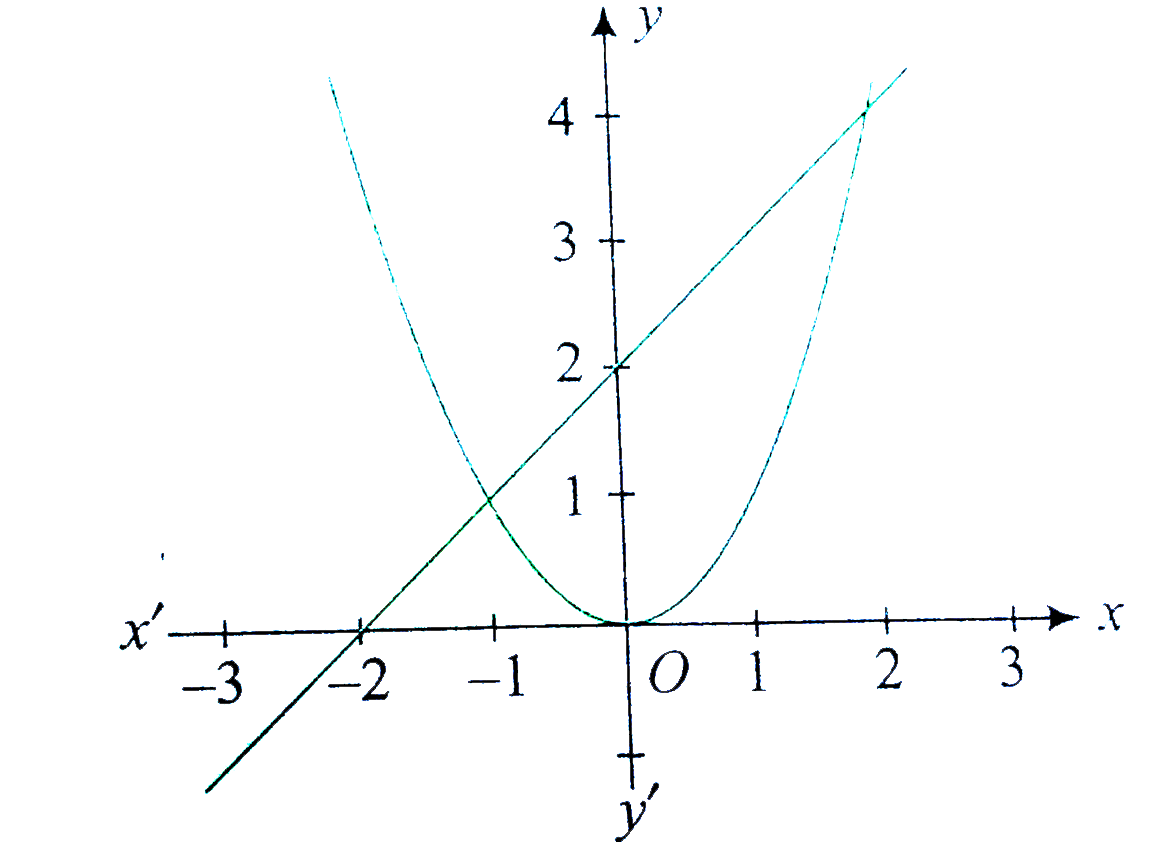
Required area =∫−1−2(x+2)dx+∫0−1x2dx
=∣∣∣x22+2x∣∣∣−1−2+∣∣∣x33∣∣∣0−1
=(12−2)−(2−4)+(0+13)
=56 sq. units.
|
Topper's Solved these Questions
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.2
Explore 14 Videos
- AREABook:CENGAGEChapter:AREAExercise:Exercise 9.3
Explore 7 Videos
- AREABook:CENGAGEChapter:AREAExercise:Comprehension Type
Explore 2 Videos
- APPLICATIONS OF DERIVATIVESBook:CENGAGEChapter:APPLICATIONS OF DERIVATIVESExercise:Question Bank
Explore 29 Videos
- AREA UNDER CURVESBook:CENGAGEChapter:AREA UNDER CURVESExercise:Question Bank
Explore 20 Videos
Similar Questions
Find the area enclosed by the curves x2=y,y=x+2,andx−aξs.
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionFind the area enclosed by the curve x=3cost,y=2sint
View SolutionFind the area enclosed by the curves 3x2+5y=32 and y=|x−2|.
View SolutionFind the area enclosed by the curves
max(|x|,|y|)=1
View SolutionFind the area enclosed by the curves
max(2|x|,2|y|)=1
View SolutionFind the area enclosed by the curves y=|x−1|andy=−|x−1|+1.
View SolutionFind the area enclosed by the curves
max(|x+y|,|x−y|)=1
View SolutionFind the area enclosed by the curve x2=4y and the abcissa y=1
View SolutionUsing integration, find the area enclosed by the curve y=cos,y=sinx and x - axis in the interval [0,π/2].
View Solution

