Find the area bounded by the y-axis, y=cosx,andy=sinxwhen0≤x≤π2.
A
2(√2−1)
B
√2−1
C
√2+1
D
√2
Video Solution
Text Solution
The correct Answer is:B
Given curves y=sinx and y−cosx meet
wher sinx=cosx
and tanx=1
⇒x=π4
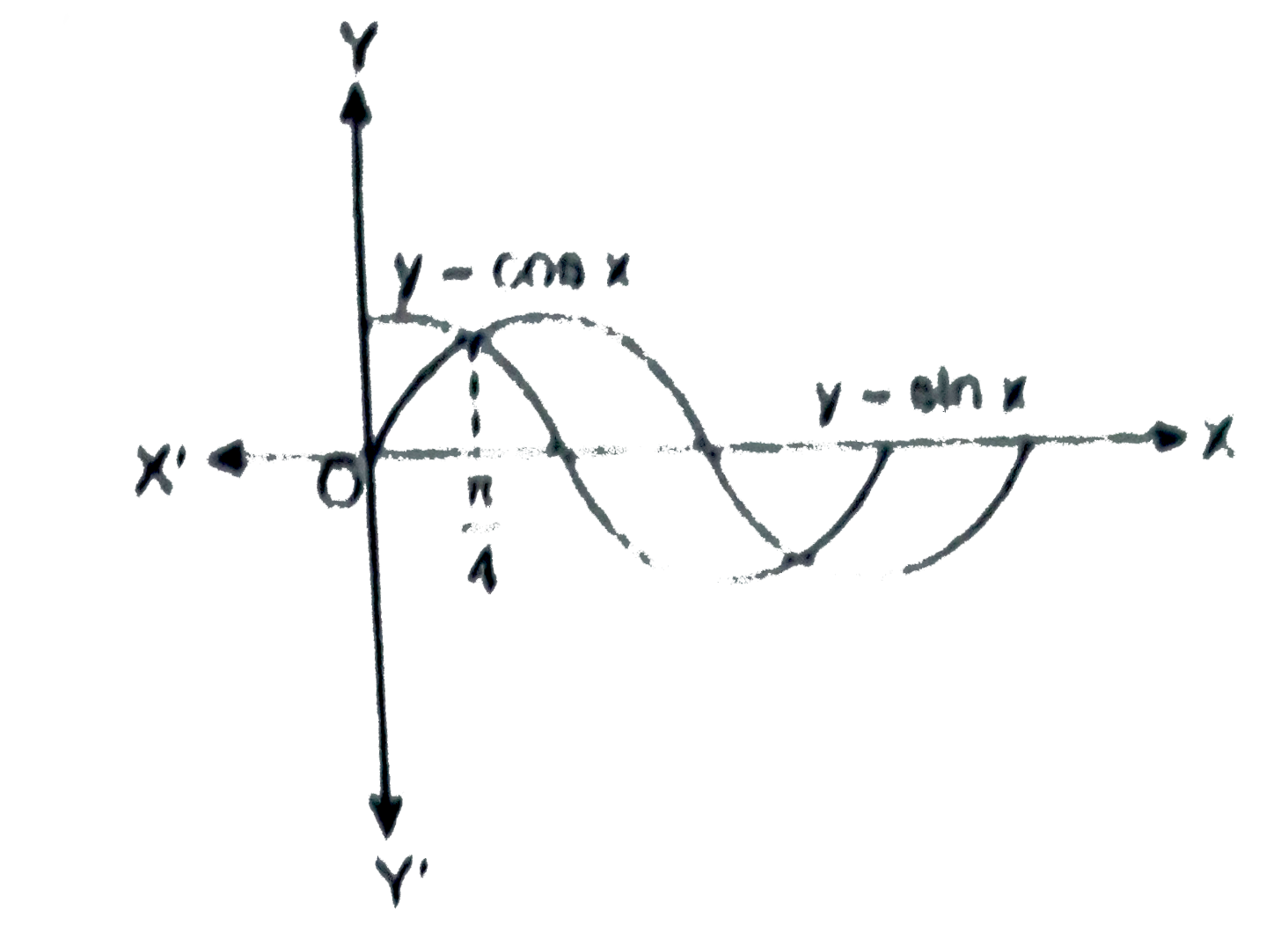
∴ Area of required shaded region
=∫π/20(cosx−sinx)dx=[sinx+cosx]π/40
=sinπ4+cosπ4−(0+1)=1√2+1√2−1
=2√2−1=√2−1 sq. units.
|
Topper's Solved these Questions
- APPLICATIONS OF INTEGRALSBook:NAGEEN PRAKASHAN ENGLISHChapter:APPLICATIONS OF INTEGRALSExercise:Exercise 8.2
Explore 7 Videos
- APPLICATIONS OF DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:APPLICATIONS OF DERIVATIVESExercise:Miscellaneous Exercise
Explore 24 Videos
- Continuity and DifferentiabilityBook:NAGEEN PRAKASHAN ENGLISHChapter:Continuity and DifferentiabilityExercise:Miscellaneous Exercise
Explore 23 Videos
Similar Questions
Find the area bounded by the y-axis, y=cosx ,and y=sinx when 0≤x≤π2.
View SolutionFind the area bounded by the curves y=xandy=x3.
View SolutionFind the area bounded by y=cosx,y=x+1,y=0
View SolutionFind the area bounded by the curves y=6x−x2andy=x2−2x.
View SolutionThe area bounded by y=tanx,y=cotx, X-axis in 0≤x≤π2 is
View SolutionFind the area bounded by the curve x2=y,x2=−yandy2=4x−3
View SolutionFind the area bounded by the curve y=sin−1x and the line x=0,|y|=π2.
View SolutionFind the area bounded by the curve y=sin−1x and the line x=0,|y|=π2.
View SolutionThe area bounded by the curves y=cosx and y=sinx between the ordinates x=0 and x=3π2 is
View SolutionFind the area bounded by y=1+2sin2x,X-axis,X=0 and x=π.
View Solution

