Question

Find the area of the region $\{(x,y):y^2\le 4x,4x^2+4y^2\le 9\}$

Explanation

Corrosponding equations of curves
`y^(2)=4x`
and `4x^(2)+4y^(2)=9`
On solving, the points of intersections are
`A((1)/(2), sqrt(2))" and "B((1)/(2), -sqrt(2))`
The centre is (0, 0) and radius is `(3)/(2)` of the given circle.

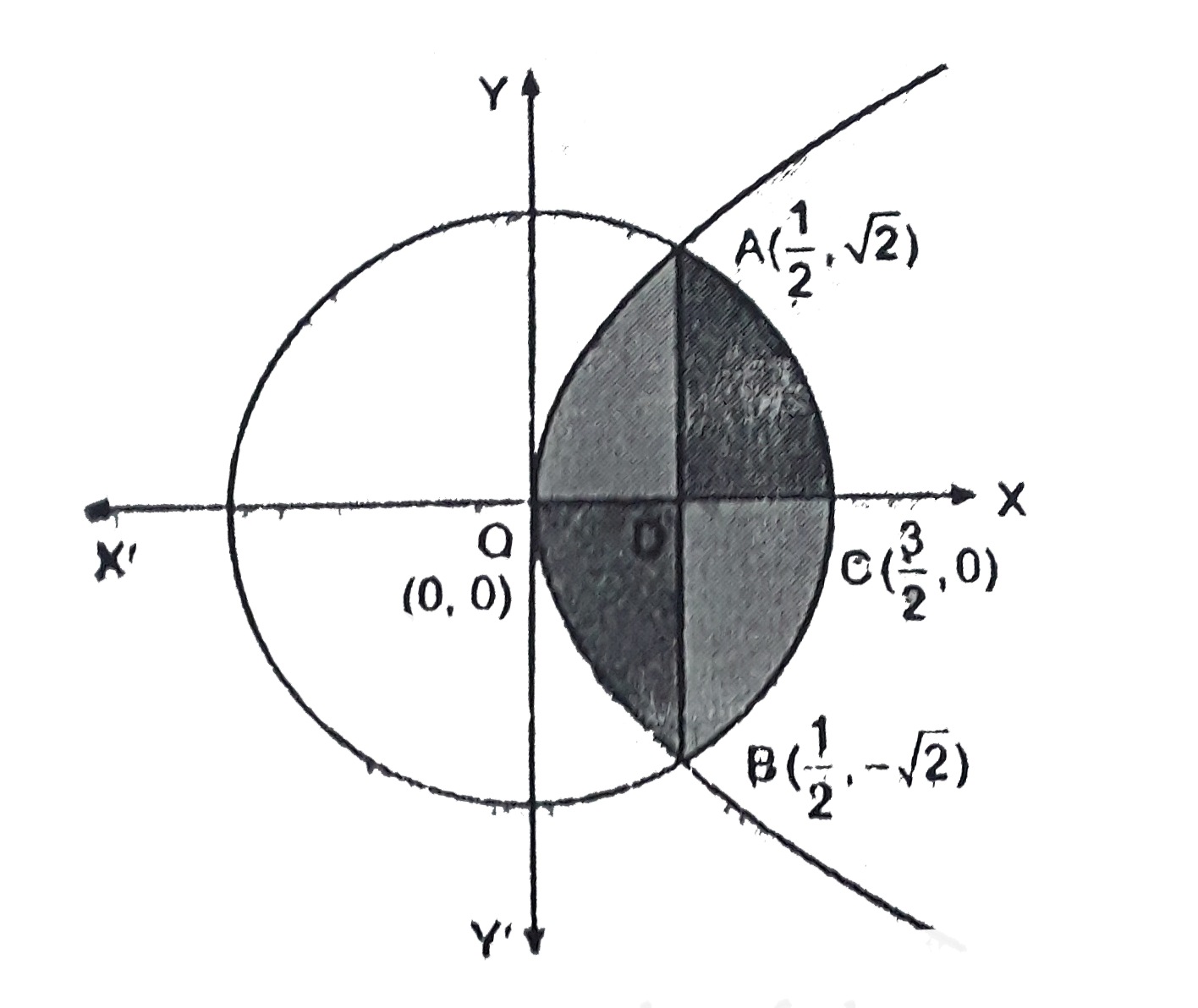
Now we draw the graphs of the curves. Using inequations, we find the required region.
Required region is symmetric about X-axis.
Required area
`=2 `area of (ODAO)`+2` area of (DCAD)
`=int_(0)^(1//2)2sqrt(x)dx+2int_(1//2)^(3//2)sqrt((9)/(4)-x^(2))dx`
`=4*(2)/(3)[x^(3//2)]_(0)^(1//2)+2[(x)/(2)sqrt((9)/(4)-x^(2))+(9)/(8)"sin"^(-1)((x)/(3//2)]_(1//2)^(3//2)`
`=(8)/(3)*(1)/(2sqrt(2))+2[(0+(9)/(8)"sin"^(-1)(1))-((1)/(4)sqrt(2)+(9)/(8)"sin"^(-1)(1)/(3))]`
`=(4)/(3sqrt(2))+(9pi)/(8)-(sqrt(2))/(2)-(9)/(4)"sin"^(-1)(1)/(3)` sq. units.
`=(4sqrt(2))/(6)-(sqrt(2))/(2)+(9)/(4)((pi)/(2)-"sin"^(-1)(1)/(3))`
`=((sqrt(2))/(6)+(9)/(4)"cos"^(-1)(1)/(3))` sq. units.