AB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : ∠APB=60∘
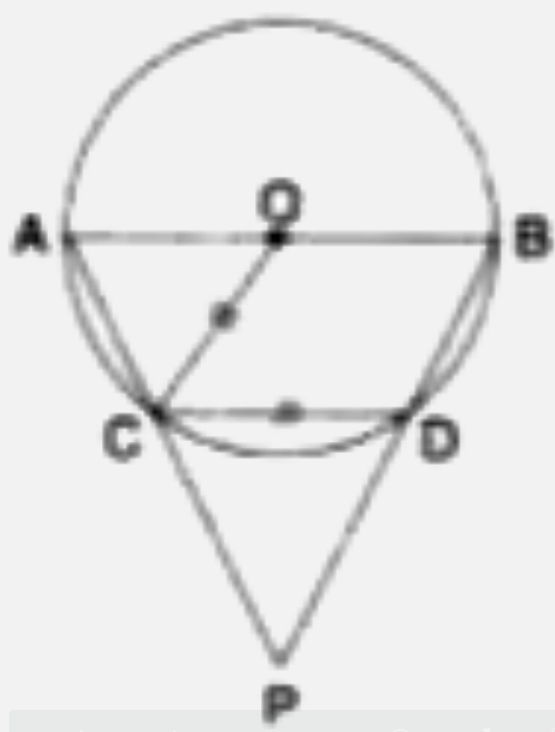
Step by step video & image solution for AB is a diameter of a circle with centre O. Chord CD is equal to radius OC. AC and BD produced intersect at P. Prove that : angleAPB= 60^(@) by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CHAPTERWISE REVISION EXERCISEBook:ICSEChapter:CHAPTERWISE REVISION EXERCISEExercise:CHAPTERWISE REVISION EXERCISE (TANGENTS AND INTERSECTING CHORDS)
Explore 10 Videos
- CHAPTERWISE REVISION EXERCISEBook:ICSEChapter:CHAPTERWISE REVISION EXERCISEExercise:CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)
Explore 3 Videos
- CHAPTERWISE REVISION EXERCISEBook:ICSEChapter:CHAPTERWISE REVISION EXERCISEExercise:CHAPTERWISE REVISION EXERCISE (LOCI)
Explore 7 Videos
- BANKING (RECURRING DEPOSIT ACCOUNTS)Book:ICSEChapter:BANKING (RECURRING DEPOSIT ACCOUNTS)Exercise:QUESTIONS
Explore 7 Videos
- CIRCLESBook:ICSEChapter:CIRCLESExercise:EXERCISE 17( C )
Explore 28 Videos
Similar Questions
AB is a diameter of the circle with centre O and chord CD is equal to radius OC (fig). AC and BD proudced meet at P. Prove that ∠CPD=60∘.
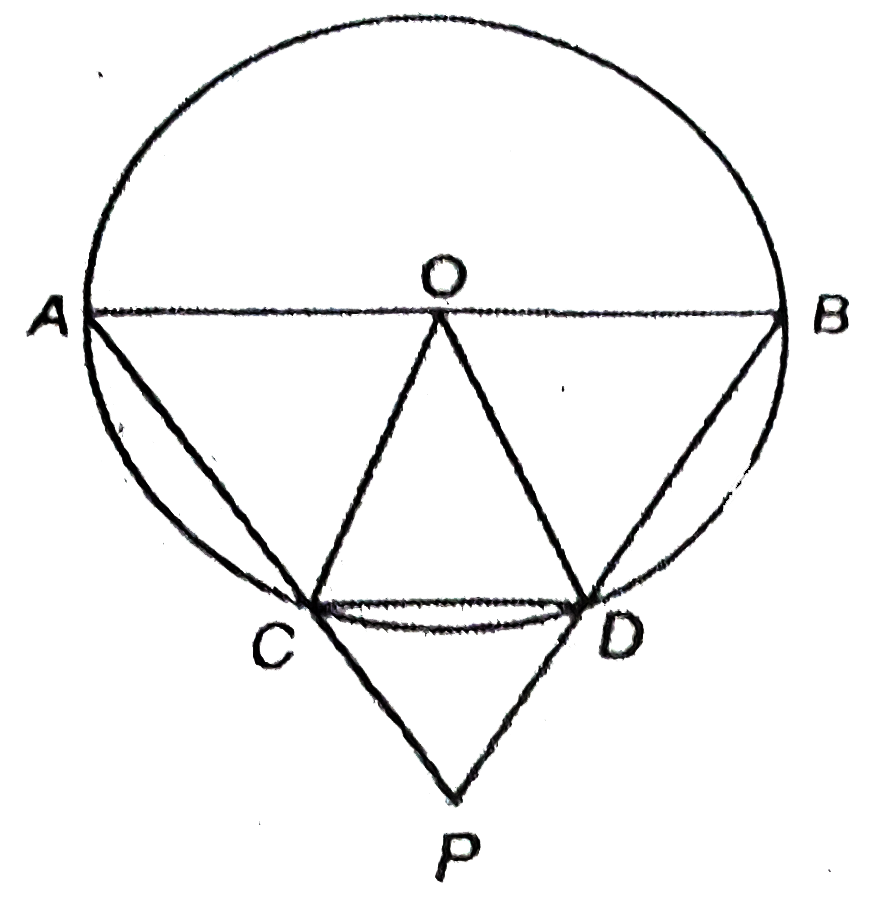
View SolutionAB is a diameter of a circle C(O, r). Chord CD is equal to radius OC. If AC and BD when produced intersect at P, prove that ∠APB is constant.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that APB=60∘ .
View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View SolutionIn the adjoining figure,AB is the diameter of the circle of centre O & the chord CD is equal to radius. If P is an external point, then find the value of ∠APB.
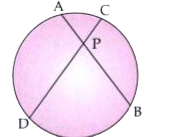
View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

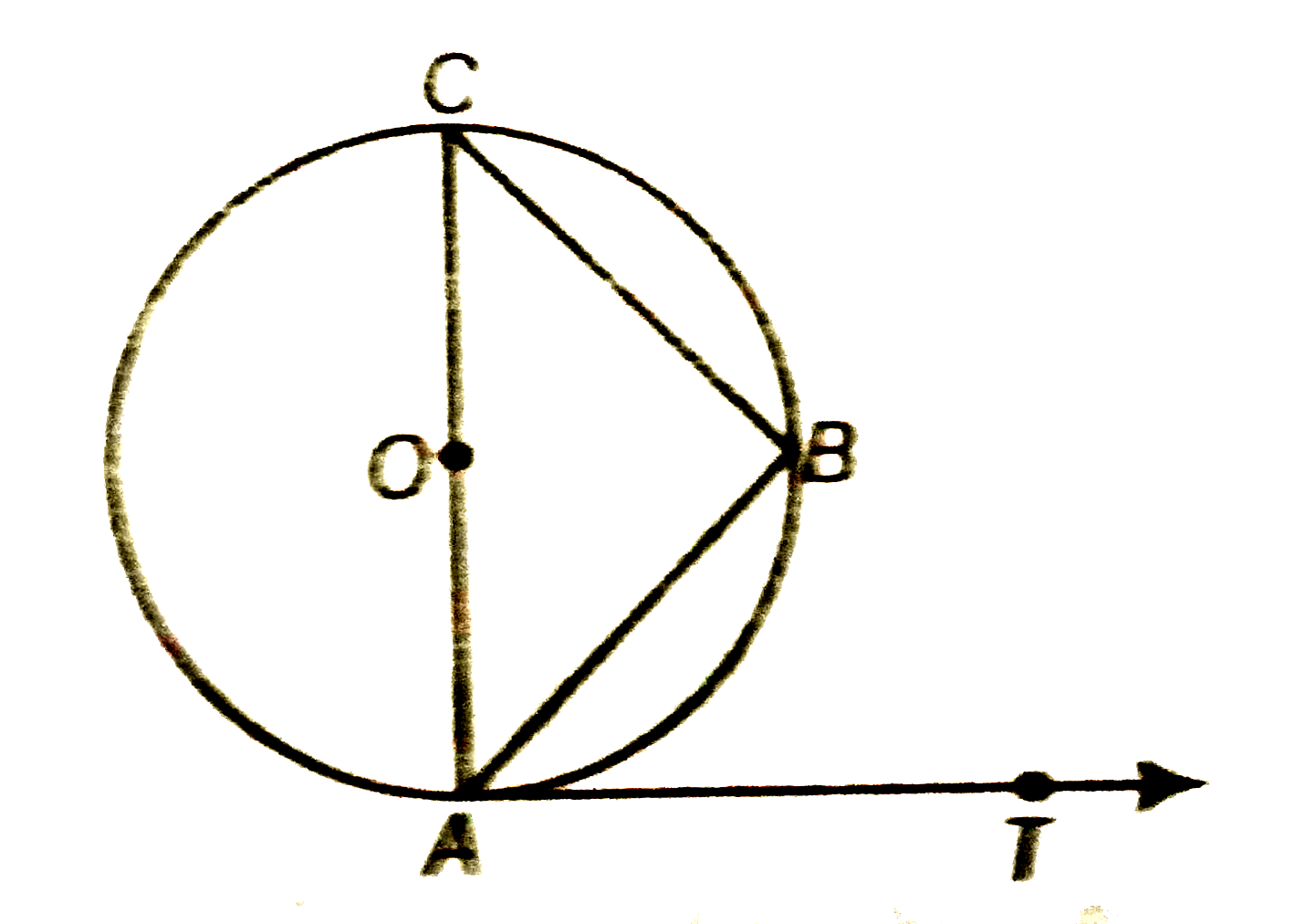
View SolutionIf AB is chord of a circle with centre O, AOC is a diameter and AT is the tangent at A as shown in figure. Prove that ∠BAT=∠ACB.
View SolutionIn the given figure AB is the diameter of a circle with centre O . If chord AC = chord AD, prove that :
(i) are BC=areDB
(ii) AB is bisector of ∠CAD.
Further, if the length of are AC is twice the length of are BC , find :
(i) ∠BAC
(ii) ∠ABC
View Solution

