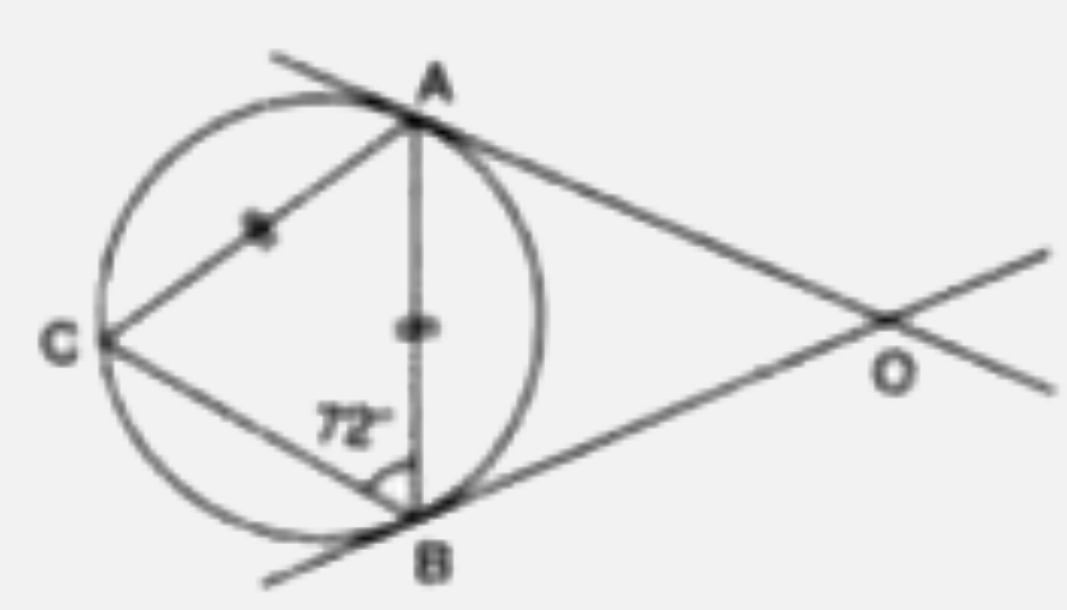
In the given figure, AC= AB and . OA and OB are two tangents. Determine:
The correct Answer is:
Step by step video & image solution for In the given figure, AC= AB and angleABC= 72^(@). OA and OB are two tangents. Determine: angleAOB by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)3videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (MENSURATION)8videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CIRCLES)9videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - BANKING (RECURRING DEPOSIT ACCOUNTS)EXERCISE - QUESTIONS7videos
BANKING (RECURRING DEPOSIT ACCOUNTS)
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )28videos
CIRCLES
Similar Questions
In the given figure, AC= AB and ∠ABC=72∘. OA and OB are two tangents. Determine:

angle subtended by the chord AB at the centre.View SolutionIn the given figure, AB = BC = DC and ∠AOB=50∘

∠AOC =?View SolutionIn the given figure AC = BD, prove that AB = CD.
 View Solution
View SolutionIn the given figure, if AB=AC, rove that BE=EC.
 View Solution
View SolutionIn the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:
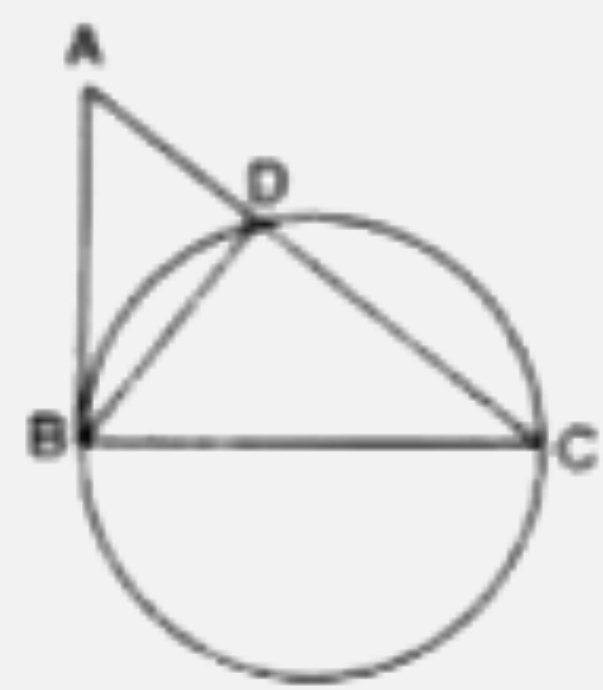
AC×AD=AB2View SolutionIn the given figure if AP=10cm. Find BP.
Given OA=6cm and OB=3cm.
 View Solution
View SolutionIn the given figure, ∠ABC=90∘ and BC is diameter of the given circle. Show that:

AC×CD=BC2View SolutionIn the given figure, PA and PB are tangents to a circle with centre O. Prove that ∠APB and ∠AOB are supplementary.
 View Solution
View SolutionIn the figure given below, O is the centre of the circle and Ab is a diameter.
If AC = BC and ∠AOC=72∘. Find:
(i) ∠ABC
(ii) ∠BAD
(iii) ∠ABD
 View Solution
View SolutionIn the given figure below, if AC = BD then prove that AB = CD.
 View Solution
View Solution
