AB and CD are two chords of a circle intersecting at a point P inside the circle. If
AP=3cm, PB= 2.5cm and CD= 6.5 cm, determine CP.
The correct Answer is:5cm or 1.5cm
To find the length of CP in the given problem, we can use the property of intersecting chords in a circle. According to this property, if two chords AB and CD intersect at point P, then the products of the lengths of the segments of each chord are equal.
1. Identify the given lengths:
- AP = 3 cm
- PB = 2.5 cm
- CD = 6.5 cm
2. Calculate the total length of chord AB:
- The total length of chord AB can be calculated as:
AB=AP+PB=3 cm+2.5 cm=5.5 cm
3. Let CP = x cm.
- Since CD = 6.5 cm, we can express DP (the other segment of chord CD) as:
DP=CD−CP=6.5 cm−x
4. Apply the intersecting chords theorem:
- According to the theorem, we have:
AP×PB=CP×DP
- Substituting the known values:
3 cm×2.5 cm=x×(6.5 cm−x)
- This simplifies to:
7.5=x(6.5−x)
5. Rearranging the equation:
- Expanding the right side:
7.5=6.5x−x2
- Rearranging gives us:
x2−6.5x+7.5=0
6. Solve the quadratic equation:
- We can use the quadratic formula x=−b±√b2−4ac2a where a=1,b=−6.5,c=7.5:
x=6.5±√(−6.5)2−4⋅1⋅7.52⋅1
- Calculate the discriminant:
(−6.5)2−4⋅1⋅7.5=42.25−30=12.25
- Now substituting back into the formula:
x=6.5±√12.252
- Since √12.25=3.5:
x=6.5±3.52
7. Calculate the two possible values for x:
- First value:
x=6.5+3.52=102=5
- Second value:
x=6.5−3.52=32=1.5
8. Conclusion:
- Therefore, the possible lengths for CP are:
CP=5 cm or 1.5 cm
- AP = 3 cm
- PB = 2.5 cm
- CD = 6.5 cm
- The total length of chord AB can be calculated as:
AB=AP+PB=3 cm+2.5 cm=5.5 cm
- Since CD = 6.5 cm, we can express DP (the other segment of chord CD) as:
DP=CD−CP=6.5 cm−x
- According to the theorem, we have:
AP×PB=CP×DP
- Substituting the known values:
3 cm×2.5 cm=x×(6.5 cm−x)
- This simplifies to:
7.5=x(6.5−x)
- Expanding the right side:
7.5=6.5x−x2
- Rearranging gives us:
x2−6.5x+7.5=0
- We can use the quadratic formula x=−b±√b2−4ac2a where a=1,b=−6.5,c=7.5:
x=6.5±√(−6.5)2−4⋅1⋅7.52⋅1
- Calculate the discriminant:
(−6.5)2−4⋅1⋅7.5=42.25−30=12.25
- Now substituting back into the formula:
x=6.5±√12.252
- Since √12.25=3.5:
x=6.5±3.52
- First value:
x=6.5+3.52=102=5
- Second value:
x=6.5−3.52=32=1.5
- Therefore, the possible lengths for CP are:
CP=5 cm or 1.5 cm
Topper's Solved these Questions
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CONSTRUCTION)3videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (MENSURATION)8videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - CHAPTERWISE REVISION EXERCISEEXERCISE - CHAPTERWISE REVISION EXERCISE (CIRCLES)9videos
CHAPTERWISE REVISION EXERCISE
- BOOK - ICSECHAPTER - BANKING (RECURRING DEPOSIT ACCOUNTS)EXERCISE - QUESTIONS7videos
BANKING (RECURRING DEPOSIT ACCOUNTS)
- BOOK - ICSECHAPTER - CIRCLESEXERCISE - EXERCISE 17( C )28videos
CIRCLES
Similar Questions
AB and CD are two chords of a circle intersecting at a point P inside the circle. If
AB= 24cm, AP= 4cm and PD = 8cm, determine CPView SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PA= 8cm, PC= 5cm and PD= 4cm, determine AB.View SolutionAB and CD are two chords of a circle intersecting at a point P outside the circle. If
PC=30cm, CD=14cm and PA=24cm, determine AB.View SolutionAB and CD are two chords of a circle intersecting at P. Prove that AP×PB=CP×PD
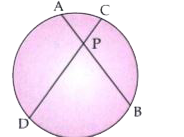 View Solution
View SolutionIn a circle, chords AB and CD intersect at a point R inside the circle. If AR : RB = 1:4 and CR: RD = 4:9, then the ratio AB: CD is
View SolutionIf chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
View SolutionAB and CD are two parallel chords of a circle which are on opposite sides of the centre such that AB=10cm, CD=24cm and the distance between AB and CD is 17cm. Find the radius of the circle.
View SolutionAB and CD are two parallel chords of a circle on opposite sides of a diameter such that AB = 24 cm and CD = 10 cm. If the radius of the circle is 13 cm, find the distance between the two chords.
View SolutionIn the figure given below, O is the centre of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD
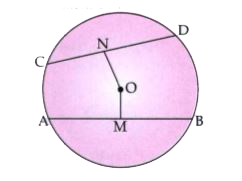 View Solution
View SolutionTwo equal chord AB and CD of a circle with centre O, intersect each other at point P inside the circle.

Prove that:
BP=DPView Solution

