Question

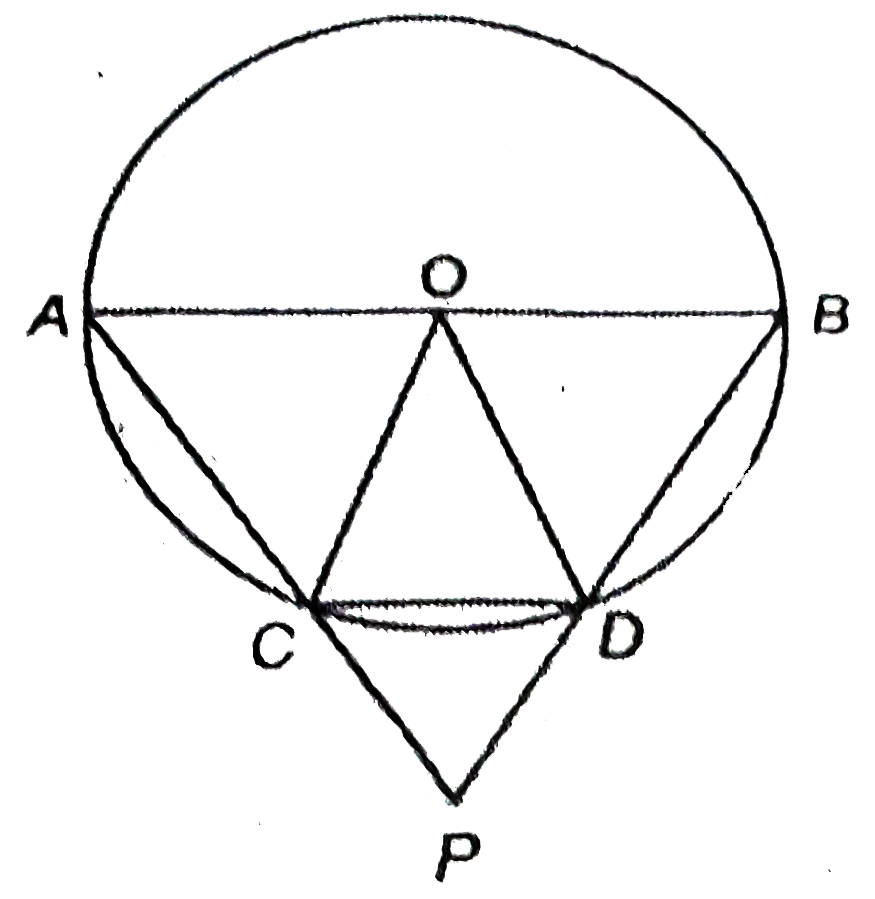
ABCD is a cyclic quadrilateral of a circle with centre O such that AB is a diameter of this circle and the length of the chord CD is equal to the radius of the circle. If AD and BC produced meet at P, show that $APB={60}^{\circ }$ .

Answer

` (ii) x+2y = 90 ^(@) `

Explanation

To solve the problem, we will follow these steps:

Step 1: Understand the given information
We have a cyclic quadrilateral ABCD where AB is a diameter of the circle, and the length of the chord CD is equal to the radius of the circle. We need to show that the angle APB is equal to 60 degrees, where AD and BC produced meet at point P.

Step 2: Draw the diagram
Draw a circle with center O. Mark points A and B such that AB is the diameter. Place points C and D on the circumference such that CD is a chord equal to the radius of the circle. Extend lines AD and BC to meet at point P.

Step 3: Analyze triangle COD
Since CD is equal to the radius, we have:
- OC = OD = CD = radius (R)

This means triangle COD is an equilateral triangle because all sides are equal. Therefore, each angle in triangle COD is:
- Angle COD = Angle ODC = Angle OCD = 60 degrees.

Step 4: Analyze triangles AOD and BOC
Since O is the center of the circle and OA = OB = radius (R), triangles AOD and BOC are also isosceles triangles.

- In triangle AOD:
- Angle AOD = 60 degrees (from triangle COD).
- Therefore, Angle OAD = Angle ODA (base angles of isosceles triangle).
- Let Angle OAD = x. Then:
\( x + x + 60 = 180 \implies 2x = 120 \implies x = 60 \text{ degrees}. \)
- Thus, Angle OAD = 60 degrees.

- In triangle BOC:
- Similarly, Angle BOC = 60 degrees.
- Let Angle OBC = Angle OCB = y. Then:
\( y + y + 60 = 180 \implies 2y = 120 \implies y = 60 \text{ degrees}. \)
- Thus, Angle OBC = 60 degrees.

Step 5: Find angles BAP and PBA
Since Angle BAP = Angle OAD and Angle PBA = Angle OBC:
- Angle BAP = 60 degrees.
- Angle PBA = 60 degrees.

Step 6: Find angle APB
In triangle ABP, the sum of angles is 180 degrees:
\( \text{Angle APB} + \text{Angle BAP} + \text{Angle PBA} = 180. \)
Substituting the known values:
\( \text{Angle APB} + 60 + 60 = 180. \)
This simplifies to:
\( \text{Angle APB} + 120 = 180 \implies \text{Angle APB} = 180 - 120 = 60 \text{ degrees}. \)

Conclusion
We have shown that Angle APB = 60 degrees.