AB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tengent at C intersects AB extended at D, then BC=BD.
To Prove, BC=BD

Join BC and OC.
Given, ∠BAC=30∘
⇒∠BCD=30∘
[angle between tangent and chord is equal to angle made by chord in the alternate segment]
∴∠ACD=∠ACO+∠OCD=30∘+90∘=120∘
[∴OC⊥CDandOA=OC=radius⇒∠OAC=∠OCA=30∘]
In ΔACD, ∠CAD+∠ACD+∠ADC=180∘
[since, sum of all interior angles of a triangle is 180∘]
⇒30∘+120∘+∠ADC=180∘
⇒∠ADC=180∘−(30∘+120∘)=30∘
Now in ΔBCD ∠BCD=∠BDC=30∘
⇒BC=BD
[since, sides opposite to equal angles are equal]
Topper's Solved these Questions
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.3 SHORT ANSWER TYPE QUESTIONS
Explore 10 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS
Explore 14 Videos
- CIRCLESBook:NCERT EXEMPLAR ENGLISHChapter:CIRCLESExercise:EXERCISE 9.4 LONG ANSWER TYPE QUESTIONS
Explore 14 Videos
- ARITHMETIC PROGRESSIONSBook:NCERT EXEMPLAR ENGLISHChapter:ARITHMETIC PROGRESSIONSExercise:Long Answer Type Questions
Explore 10 Videos
- CONSTRUCTIONSBook:NCERT EXEMPLAR ENGLISHChapter:CONSTRUCTIONSExercise:Exercise 10.4 Long Answer type Questions
Explore 7 Videos
Similar Questions
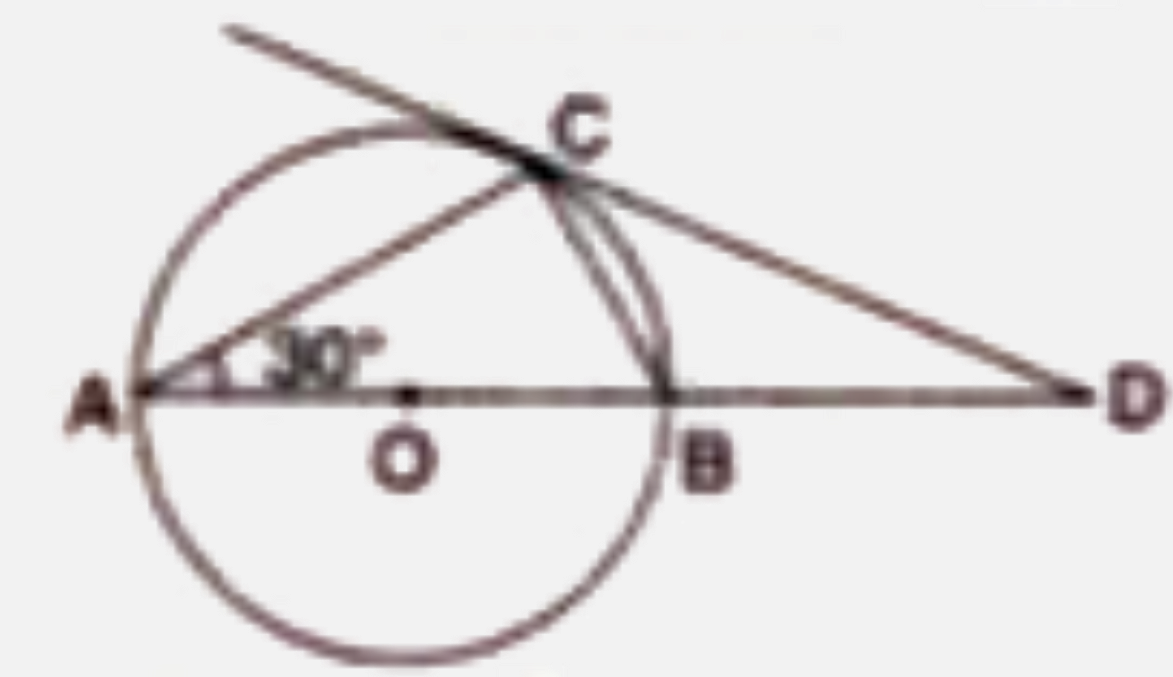
In the given figure AB is the diameter and AC is the chord of a circle such that ∠BAC=30∘. The tangent at C intersects AB produced at D. Prove that :BC=BD.
View SolutionIn figure, AB is a chord of the circle and AOC is its diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then ∠BAT is equal to
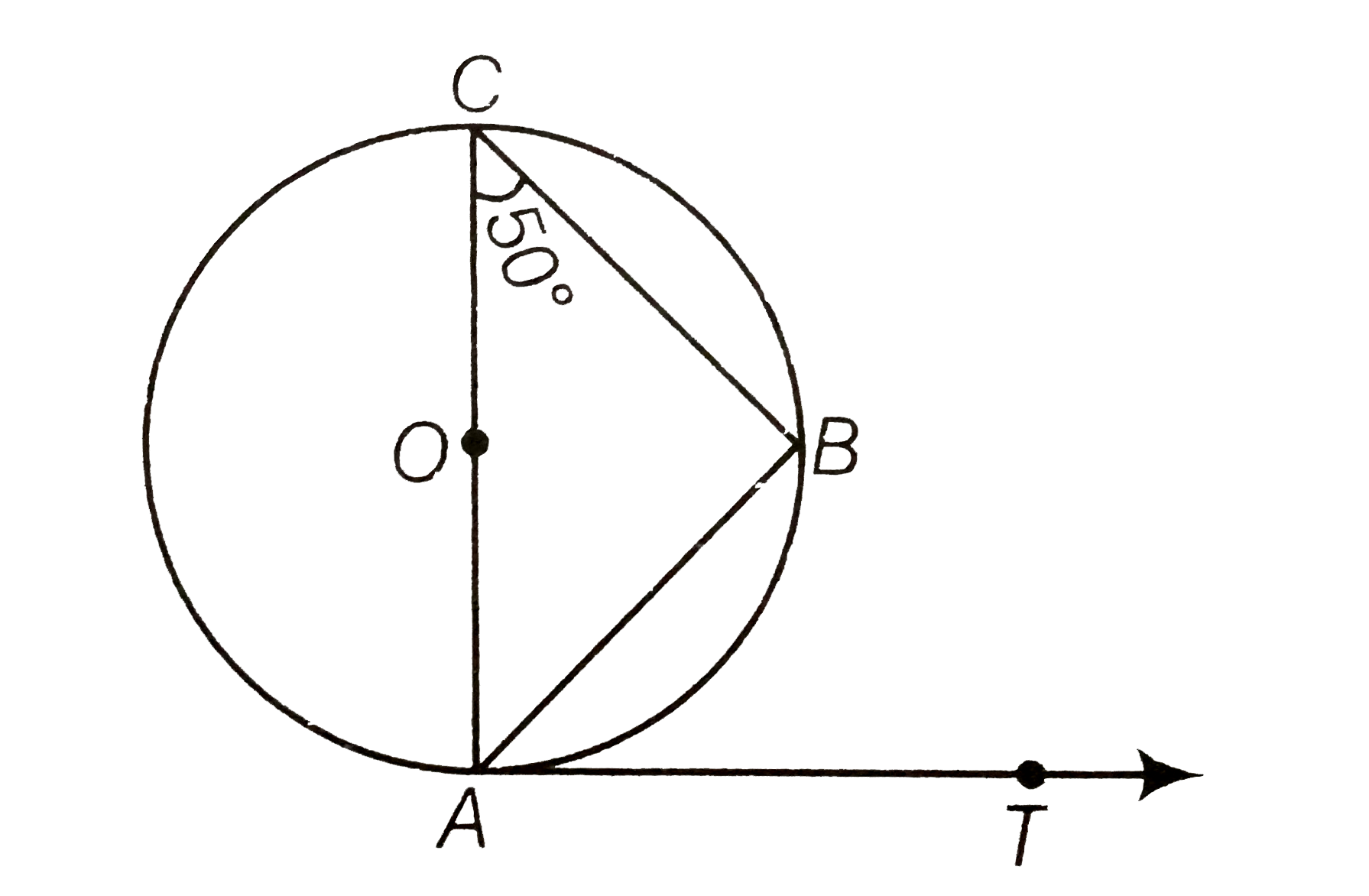
View SolutionIn figure, AB is a chord of the circle and AOC is the diameter such that ∠ACB=50∘. If AT is the tangent to the circle at the point A, then angleBAT is equal to : (a) 45∘ , (b) 60∘ , (c) 50∘ , (d) 55∘
View SolutionAB is the diameter and AC is a chord of a circle with centre O such that angle BAC=30∘. The tangent to the circle at C intersects AB produced in D. Show that BC=BD.
View SolutionAB is a diameter of a circle. CD is a chord parallel to AB and 2CD=AB. The tangent at B meets the line AC produced at E then AE is equal to -
View SolutionIf AOB is a diameter of a circle and C is a point on the circle, then AC2+BC2=AB2.
View SolutionIn the adjoinig figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘.

View SolutionIn Figure, AB is a diameter of the circle, CD is a chord equal to the radius of the circle. AC and BD when extended intersect at a point E. Prove that ∠AEB=60∘
View SolutionAD is a diameter of a circle and AB is a chord. If AD = 34cm, AB = 30cm, the distance of AB form the centre of the circle is
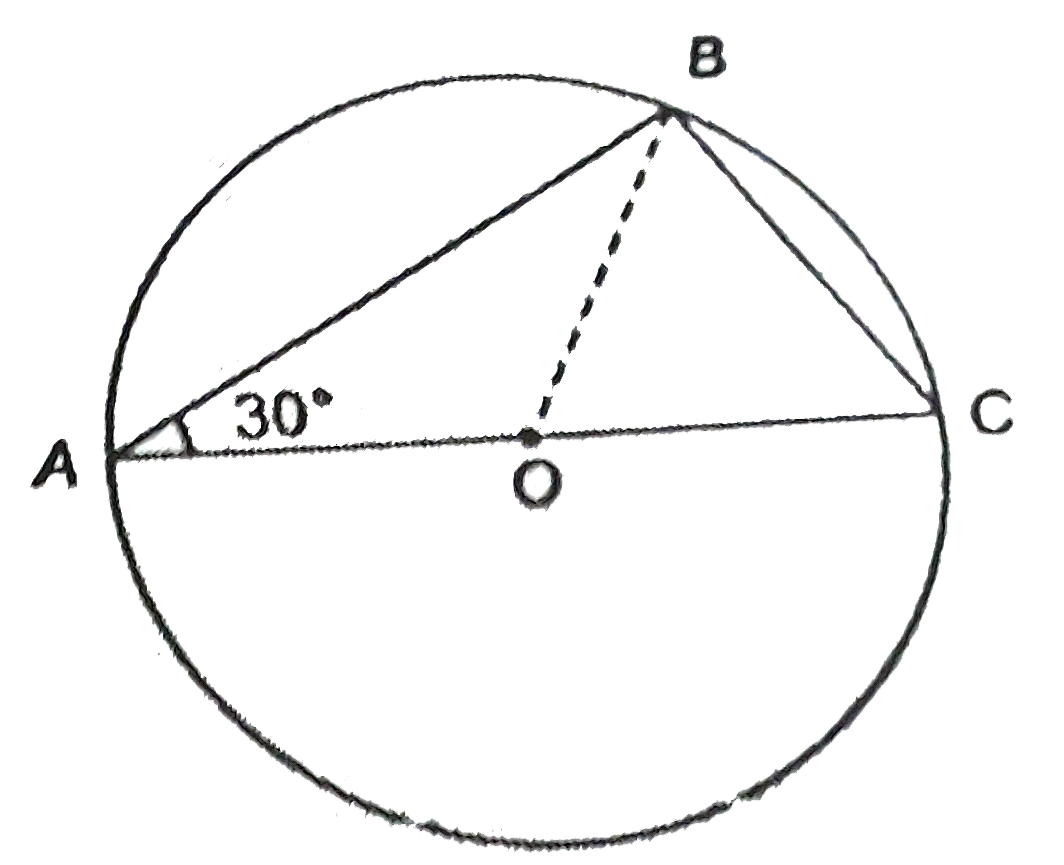
View SolutionIn the adjoining figure, O is the centre of the circle and AC is its diameter. If ∠BAC=30∘, then find ∠BOC.
View Solution

