A beam is supported at its ends by supports which are 12 metres apart. Since the load is concentrated at its centre, there is a deflection of 3 cm at the centre and the deflected beam is in the shape of a parabola. How far from the centre is the
Let equation of parabola is x2=ay
It passes through the point A (600,3)
∴ (600)2=4a(3)
⇒ 4a=120000
Therefore, x2=120000y
Let at 1 cm deflection there is a point B then BO=2cm
Let the co-ordinates of B are (h,2).
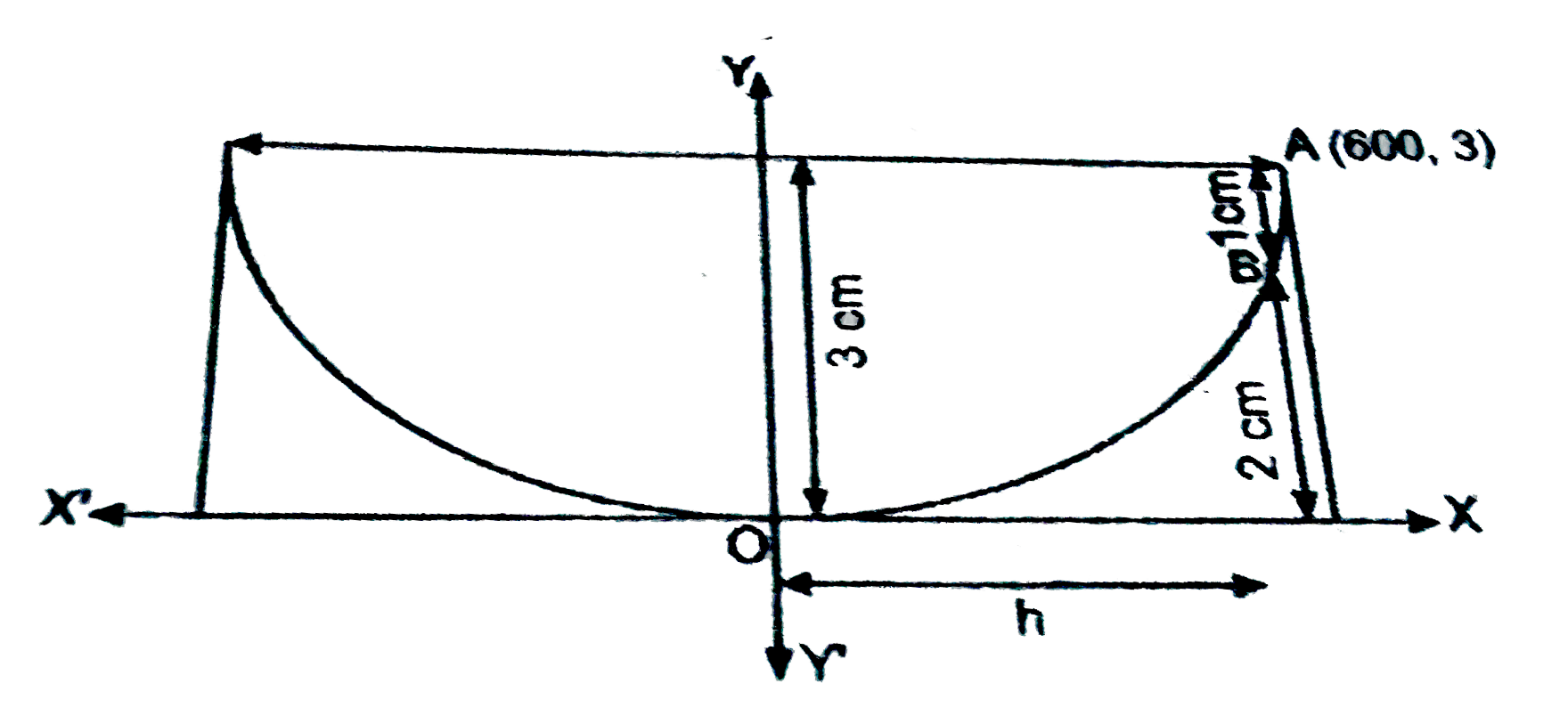
B lies on parabola (1)
∴ h2=120000×2=240000
⇒ h=200√6cm=2√6m
Therefore, 1 cm deflection is at a distance of 2√6m
from the centre.
Topper's Solved these Questions
- CONIC SECTIONBook:NAGEEN PRAKASHANChapter:CONIC SECTIONExercise:Exercise 11A
Explore 38 Videos
- CONIC SECTIONBook:NAGEEN PRAKASHANChapter:CONIC SECTIONExercise:Exercise 11B
Explore 23 Videos
- CONIC SECTIONBook:NAGEEN PRAKASHANChapter:CONIC SECTIONExercise:Miscellaneous Exercise
Explore 8 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATION Book:NAGEEN PRAKASHANChapter:COMPLEX NUMBERS AND QUADRATIC EQUATION Exercise:MISCELLANEOUS EXERCISE
Explore 20 Videos
- INTRODUCTION OF THREE DIMENSIONAL GEOMETRYBook:NAGEEN PRAKASHANChapter:INTRODUCTION OF THREE DIMENSIONAL GEOMETRYExercise:Miscellaneous Exercise
Explore 6 Videos
Similar Questions
A beam is supported at its ends by supports which are 12 metres apart. Since the load is connected at its centre, there is a deflection of e centre and the deflected beam is in the shape of a parabola. How far from the centre is the deflection 1 cm?
View SolutionA beam of metal supported at the two edges is loaded at the centre. The depression at the centre is proportional to

View Solution
Knowledge Check
The radius of a circles is 13cm and the length of one of its chords is 10cm. Find the distance of the chord from the centre.
A9cmB10cmC11cmD12cmThe radius of a circle is 13 cm and the length of one of its chords is 10 cm . The distance of the chord from the centre is
A12 cmB9 cmC10 cmD15 cmA rectangular beam of metal supported at its two ends is loaded at the centre. The depression at the centre is proportional to
A1YBY2C1Y2DY
The radius of a circle is 8cm and the length of one of its chords is 12cm. Find the distance of the chord from the centre.
View SolutionFind the length of the chord of a circle of radius 12 cm if its distance from the centre is 9 cm.
View SolutionThe radius of a circle is 13 cm and the length of one of its chords is 10 cm. Find the distance of the chord from the centre.
View SolutionA chord 6 cm long is at a distance of 4 cm from the centre of a circle. Find the length of a chord which is at a distance of 3 cm from the centre of the circle.
View SolutionThe radius of a circle is 13 cm and the length of one of its chords is 10 cm . The distance of the chord from the centre is
View Solution

