A beam is supported at its ends by supports which are 12 metres apart. Since the load is concentrated at its centre, there is a deflection of 3 cm at the centre and the deflected beam is in the shape of a parabola. How far from the centre is the

Video Solution

Text Solution

Verified by Experts

Let equation of parabola is $x^{2} = a y$
It passes through the point A (600,3)
$∴ {(600)}^{2} = 4 a (3)$
$\Rightarrow 4 a = 120000$
Therefore, $x^{2} = 120000 y$
Let at 1 cm deflection there is a point B then BO=2cm
Let the co-ordinates of B are (h,2).

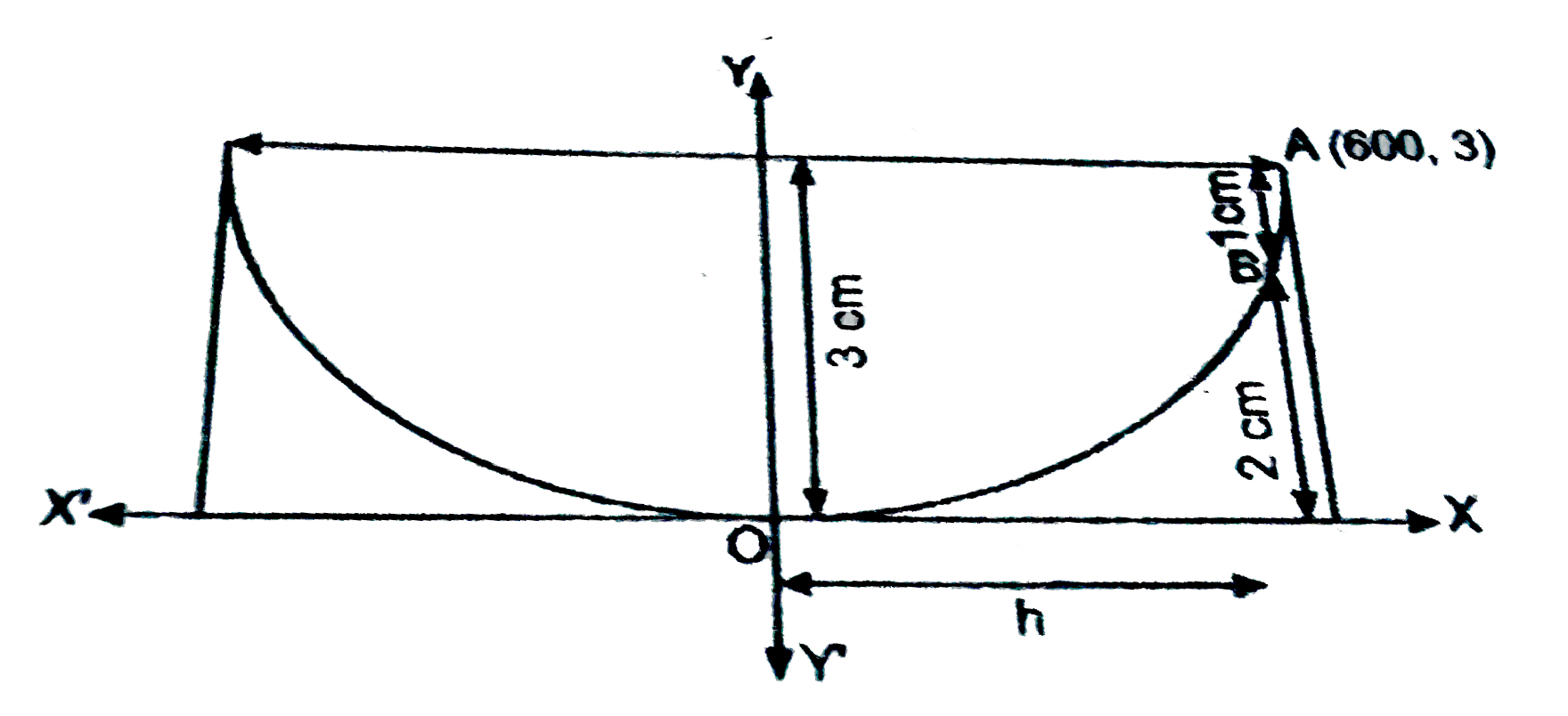
B lies on parabola (1)
$∴ h^{2} = 120000 \times 2 = 240000$
$\Rightarrow h = 200 \sqrt{6} c m = 2 \sqrt{6} m$
Therefore, 1 cm deflection is at a distance of $2 \sqrt{6} m$
from the centre.

Updated on:21/07/2023