Question

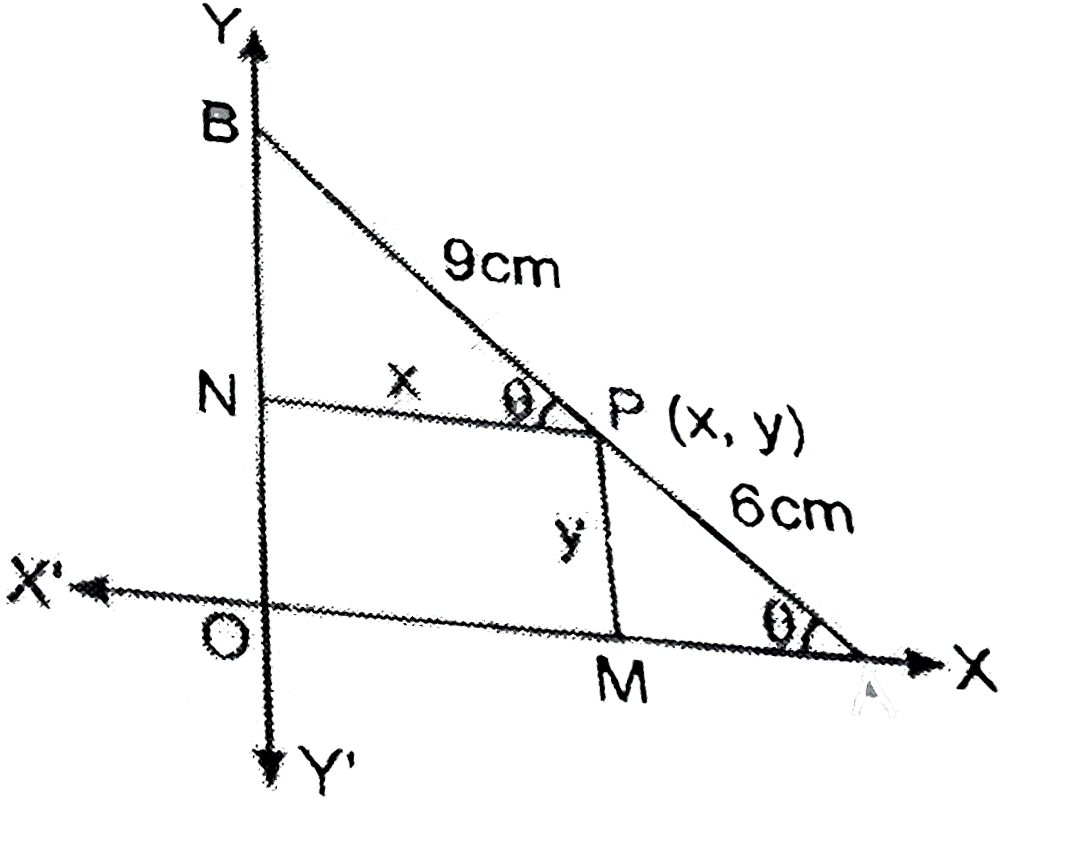
A rod AB of length 15 cm rests in between two coordinate axes in
such a way that the end point A lies on x-axis and end point B lies on
y-axis. A point P(x, y) is taken on the rod in such a way that AP = 6 cm.
Show that the locus of P is an ellip

Explanation

Let the rod AB makes an angle `theta` from x-axis.
Here AB=15 cm and AP = 6 cm
`rArr" "BP=9cm`
In `DeltaAPM`
`sintheta=(y)/(6)`
In `DeltaPBN`
`costheta=(x)/(9)`
`because" "cos^(2)theta+sin^(2)theta=1`
`rArr" "((x)/(9))^(2)+((y)/(6))^(2)=1`
`rArr" "(x^(2))/(81)+(y^(2))/(36)=1`, which is the locus of point P