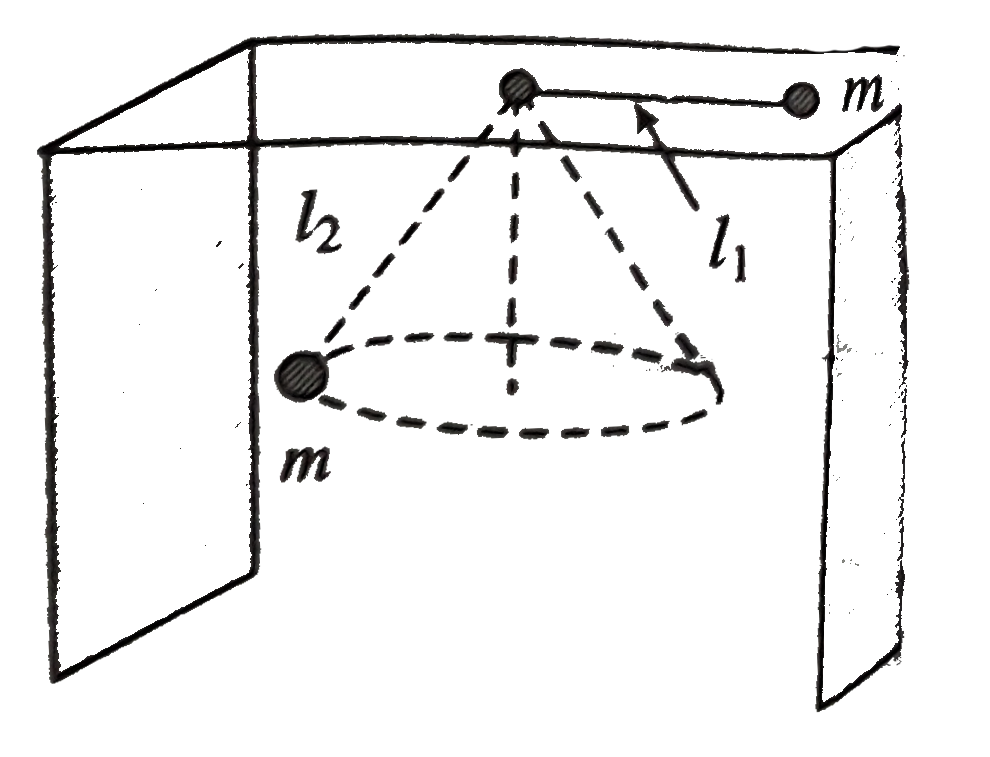
Two identical particle are attached at the ends of a light string which passes through a hole at the centre of a table another particle on the table is made to revolve with angular velocity ω1 . One of the particles is made to move in a horizontal circle as a conical pendulum with angular velocity ω2 . If l1 and l2 are the length of the string over and under the table , then in order that particle under the table neither moves down nor moves up the ratio l1l2 is :

ω1ω2
ω2ω1
ω21ω22
ω22ω21
The correct Answer is:D
For the particle on the table T = mω21l1

For the particle under the table T sin θ=mω22r
= mω22l2sinθ orT=mω22l2
∴ mω21l1=mω22l2 or l1l2=ω22ω21
Topper's Solved these Questions
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - More than one correct18videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Assertion - Reason12videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FRICTION AND CIRCULAR MOTION EXERCISE - Problem For Practice23videos
FRICTION AND CIRCULAR MOTION
- BOOK - GRB PUBLICATIONCHAPTER - FORCE AND NEWTONS LAWS OF MOTIONEXERCISE - Comprehension12videos
FORCE AND NEWTONS LAWS OF MOTION
- BOOK - GRB PUBLICATIONCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Comprehension type Queston14videos
MOTION IN A STRAIGHT LINE
Similar Questions
Two identical particles are attached at the end of a light string which passes through a hole at the center of a table One of the partical is made to move in a circle on a table with angular velocity ω1 and the ther is made a move is a horizontal ω2 if l1and l2 are the length the table , than in order that particle under down the table neither moves down nor move up the ratiol1/l2 is
 View Solution
View SolutionTwo identical particles are attached at the end of a light string which passes through a hole at the center of a table One of the partical is made to move in a circle on a table with angular velocity ω1 and the ther is made a move is a horizontal ω2 if l1and l2 are the length the table , than in order that particle under down the table neither moves down nor move up the ratiol1/l2 is
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Two identical particles are attached at the end of a light string which passes through a hole at the center of a table One of the partical is made to move in a circle on a table with angular velocity ω1 and the ther is made a move is a horizontal ω2 if l1and l2 are the length the table , than in order that particle under down the table neither moves down nor move up the ratiol1/l2 is
 Aω1ω2Bω2ω1Cω21ω22Dω22ω21
Aω1ω2Bω2ω1Cω21ω22Dω22ω21 - Question 2 - Select One
Two particles, each of mass m are attached to the two ends of a light string of length l which passes through a hole at the centre of a table. One particle describes a circle on the table with angular velocity ω1 and the other describes a circle as a conical pendulum with angular velocity ω2 below the table as shown in figure -3.86. if l1 and l2 are the lengths of the portion of the string above and below the table then :
 Al1l2=ω22ω21Bl1l2=ω21ω22C1ω21+1ω22=lgD1ω21+1ω22>lg
Al1l2=ω22ω21Bl1l2=ω21ω22C1ω21+1ω22=lgD1ω21+1ω22>lg - Question 3 - Select One or More
A particle is revolving in a circle of radius r and centre at 'O' with uniform angular velocity ω. Choose the correct option(s) :
 Athe ratio of angular velocity at A about O and about B is 3:2Bthe angular velocity at A about all points O,B and C is same.Cthe angular velocity at A about C is ω/2Dthe velocity at A and C are same.
Athe ratio of angular velocity at A about O and about B is 3:2Bthe angular velocity at A about all points O,B and C is same.Cthe angular velocity at A about C is ω/2Dthe velocity at A and C are same.
For a particle moving in a horizontal circle with constant angular velocity:
View SolutionA particle of mass m is attached to one end of a weightless and inextensible string of length L. The particle is on a smooth horizontal table. The string passes through a hole in the table and to its other and is attached a small particle of equal mass m. The system is set in motion with the first particle describing a circle on the table with constant angular velocity ω1 and the second particle moving in the horizontal circle as a conical pendulum with constant angular velocity ω2 Show that the length of the portions of the string on either side of the hole are in the ratio ω22:ω21
View SolutionA particle is revolving in a circle of radius r and centre at 'O' with uniform angular velocity ω. Choose the correct option(s) :
 View Solution
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View SolutionA particle of maas m is attched to a light string of length l, the other end of which is fixed. Initially the string is kept horizontal and the particle is given an upwrd velocity v. The particle is just able to complete a circle
View Solution
