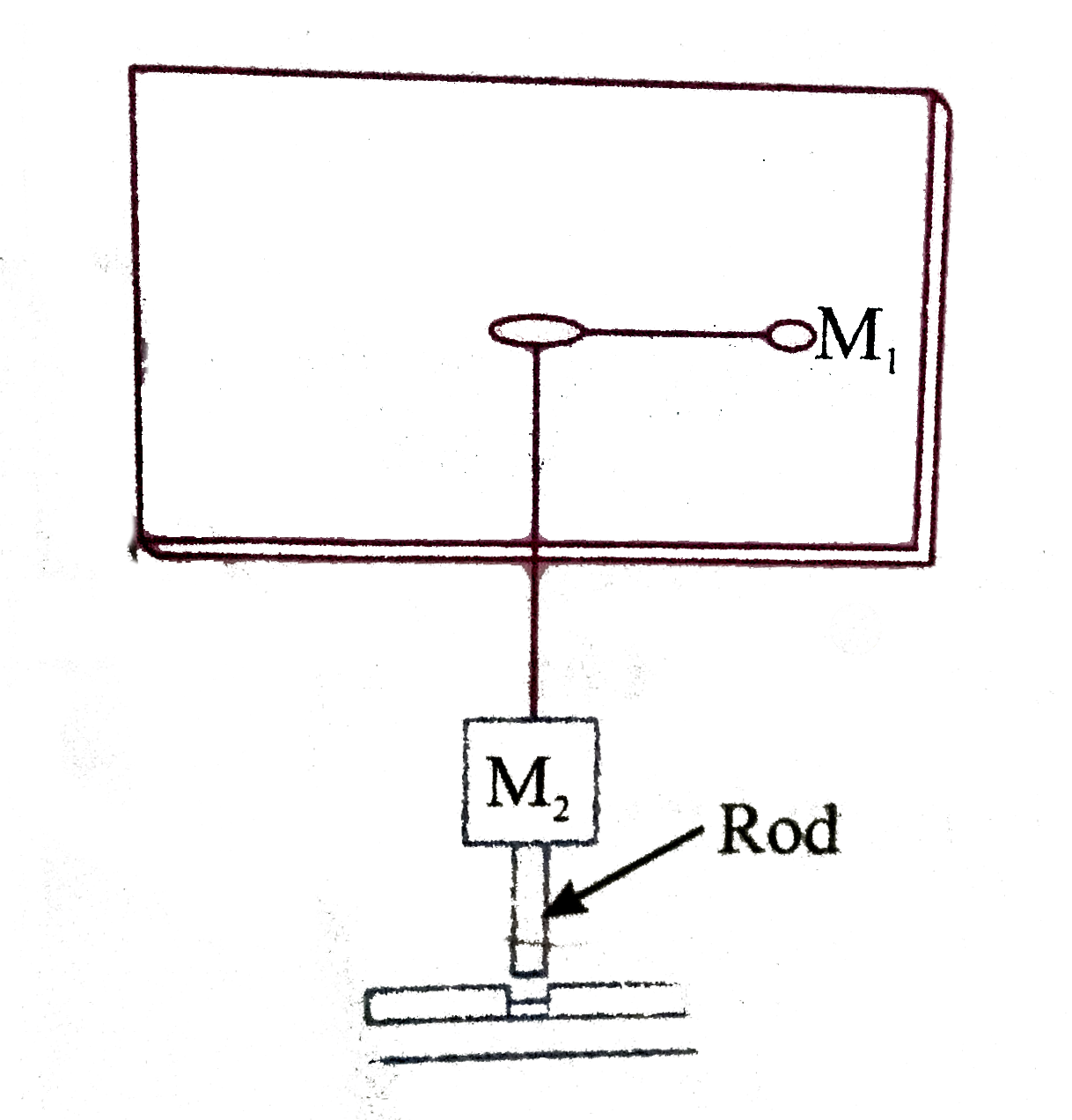
For the arrangement in the Figure, the particle M1 attached to one end of string which moves on a horizantal table in a circle of radius l2 (where l is the length of the string) with constant angular speed ω. The other end of the string attached to to mass M2 which rest on a vertical rod. When the rod collapse, the acceleration of mass M2 at that instant
g
ω2l2
2M2g−M1lω22(M1+M2)
M2g+M1lω2M1+M2
The correct Answer is:C
From Newton's second law

T−M1ω2l2=M1a and M2g−T=M2a
After solving above equations , we get
a=2M2g−M1lω22(M1+M2)
Topper's Solved these Questions
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:More than one correct
Explore 18 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Assertion - Reason
Explore 12 Videos
- FRICTION AND CIRCULAR MOTION Book:GRB PUBLICATIONChapter:FRICTION AND CIRCULAR MOTION Exercise:Problem For Practice
Explore 23 Videos
- FORCE AND NEWTONS LAWS OF MOTIONBook:GRB PUBLICATIONChapter:FORCE AND NEWTONS LAWS OF MOTIONExercise:Comprehension
Explore 12 Videos
- MOTION IN A STRAIGHT LINEBook:GRB PUBLICATIONChapter:MOTION IN A STRAIGHT LINEExercise:Comprehension type Queston
Explore 14 Videos
Similar Questions
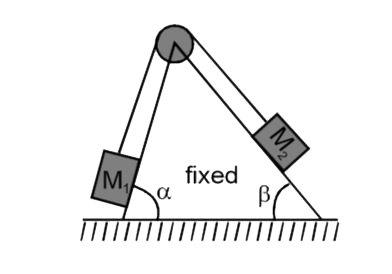
Two masses M1 and M2 are attached to the ends of a light string which passes over a massless pulley attached to the top of a double inclined smooth plane of angles of inclination α and β.The tension in the string is :
View SolutionTwo particles of mass m each are attached to a light rod of length d, one at its centre and the other at a free end, The rod is fixed at the other end is rotated in a plane at an angular speed ω. Calculate the angular momentum of the particle at the end with respect to the particle at the centre
View Solution
Knowledge Check
A stone of mass m tied to a string of length l is rotated in a circle with the other end of the string as the centre. The speed of the stone is v. If the string breaks, the stone will move
Amove towards the centreBmove away from the centreCmove along a tangentDstopA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
Am2gm1+m2Bm1gm1+m2CgDm2gm1In fig mass m is lifted up by attaching a mass 2m to the other end of the string while in fig
(b) m is lifted by pulling the other end of the string with a constant force F=2mg then:
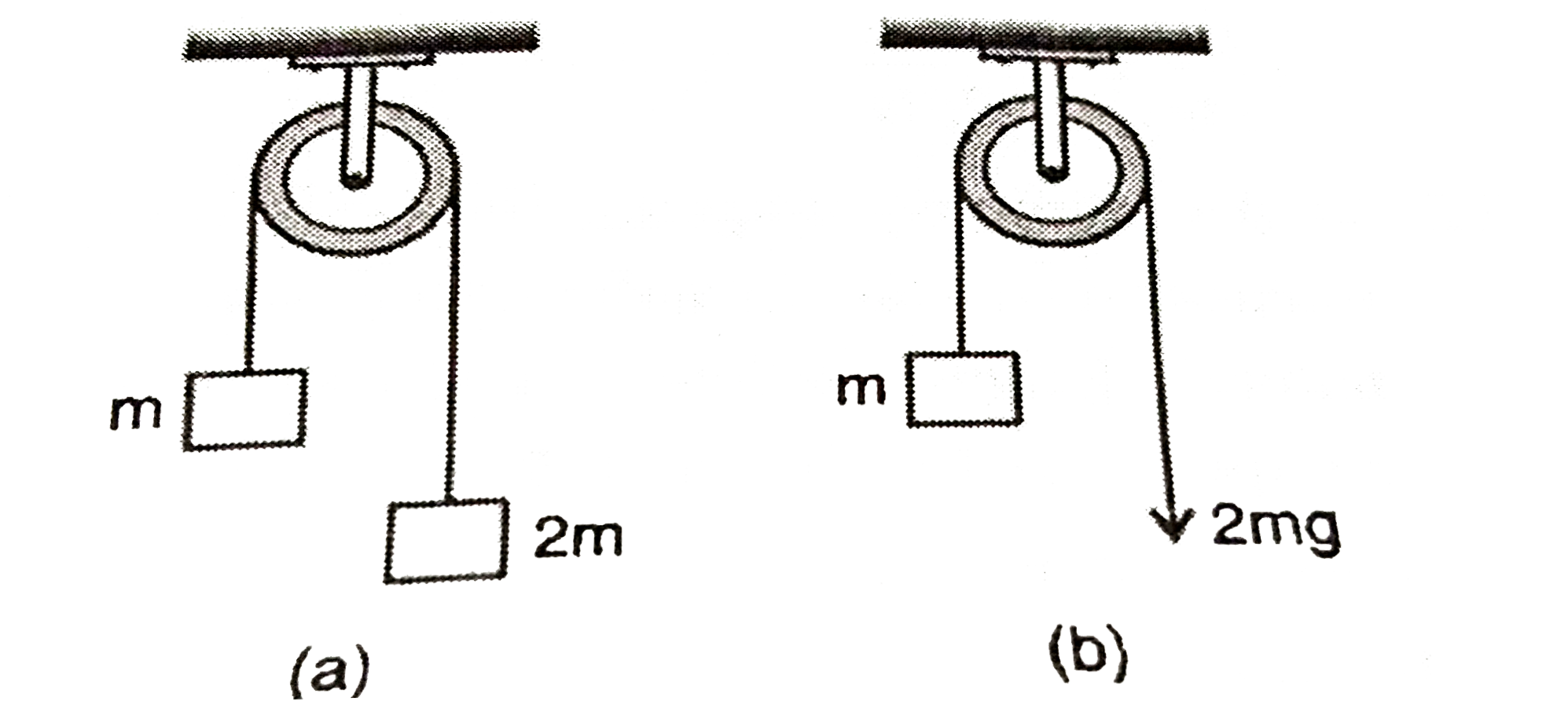 Aacceleration of m in the two situations is same and non - zeroBacceleration of m in situation
Aacceleration of m in the two situations is same and non - zeroBacceleration of m in situation
(a) is more than that of in situation(b)Cacceleration of m in situation
(a) is less than that of in situation
(b)Dacceleration of m in the two situations is same and equals to zero
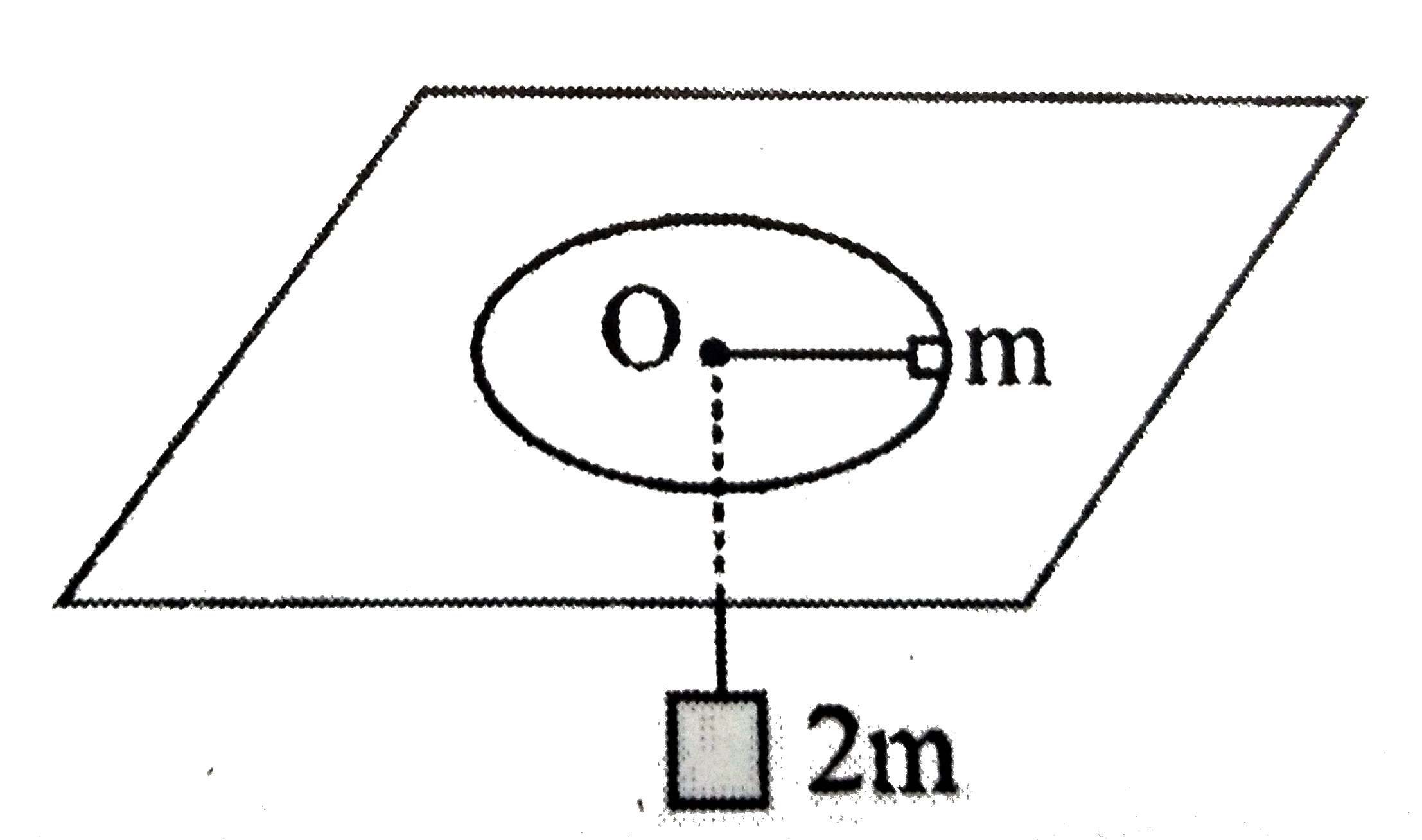
A mass m rotating freely in a horizontal circle of a radius 1m on a frictionless smooth table support a stationary mass 2m, attached to the other end of the string passing through smooth hole O in table, hanging vertically. Find the angular velocity of rotation.
View SolutionA block of mass m is attached to one end of a light string which is wrapped on a disc of mass 2m and radius R. The total length of the slack portion of the string is 1. The block is released from rest. The angular velocity of the disc just after the string becomes taut is
View SolutionA particle of mass m attached to an inextensible light string is moving in a vertical circle of radius r. The critical velocity at the highest point is v0 to complete the vertical circle. The tension in the string when it becomes horizontal is
View SolutionA mass attached to one end of a string crosses top - most point on a vertical circle with critical speed. Its centripetal acceleration when string becomes horizontal will be
(where, g=gravitational acceleration)
View SolutionA partical of mass m is attached to a massless string of length l and is oscillating in a vrtical plane with the other end of the string fixed to a rigid support. The tension in the string at a certain instant is T=kmg .
View Solution

