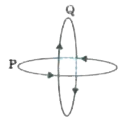
Two identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in fig. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
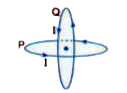
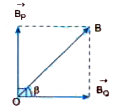
Magnetic field due to current carrying coil = Field BQ due to current carrying coil . Their directions are as shown in fig. As the two field are in mutually perpendicular directions, hence net magnetic field at the common centre O is
The net field subtend an angle from such that
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISM Book:U-LIKE SERIESChapter:MOVING CHARGES AND MAGNETISM Exercise:LONG ANSWER QUESTIONS-I
Explore 33 Videos
- MOVING CHARGES AND MAGNETISM Book:U-LIKE SERIESChapter:MOVING CHARGES AND MAGNETISM Exercise:LONG ANSWER QUESTIONS-II
Explore 11 Videos
- MOVING CHARGES AND MAGNETISM Book:U-LIKE SERIESChapter:MOVING CHARGES AND MAGNETISM Exercise:VERY SHORT ANSWER QUESTIONS
Explore 39 Videos
- MODEL TEST PAPER 3 (UNSOLVED)Book:U-LIKE SERIESChapter:MODEL TEST PAPER 3 (UNSOLVED)Exercise:SECTION A
Explore 3 Videos
- NUCLEIBook:U-LIKE SERIESChapter:NUCLEIExercise:Self Assessment Test
Explore 10 Videos
Similar Questions
Two identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
View SolutionTwo identical circular wires P and Q each of radius R and carrying current 'I' are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.

View SolutionTwo identical loops P and Q each of radius 5cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to 3A and 4A respectively.
View SolutionTwo identical loops P and Q each of radius 5cm are lying in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net field at the common centre of the two coils, if they carry currents equal to 3A and 4A respectively.

View SolutionTwo identical coils P and Q each of radius R are lying in perpendicular planes such that they have a common centre. Find the magnitude and PC direction of the magnetic field at the common centre of the two coils, if they carry currents equal to land √3I respectively.
View Solution(a) Draw the pattern of magnetic field lines for a circular coil carrying current.
(b) Two identical planes such that they have a common centre at P as shown in the figure. Find the magnitude and direction of the net magnetic field at the point P due to the loops
View SolutionAnswer the following:
(a) State Biot - Savart's law and express this law in the vector form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ planes. Find the magnitude and direction of the net magnetic field at the centre of the coils.
View Solution(a) State Biot - Savart law and express this law in the vactor form.
(b) Two identical circular coils, P and Q each of radius R, carrying currents 1A and √3A
respectively, are placed concentrically and perpendicular to each other lying in the XY
and YZ planes. Find the magnitude and direction of the net magnetic field at the centre
of the coils.
View SolutionTwo identical circular coils, P and Q, carrying currents 1A and √3A respectively, are placed concentrically and perpendicular to each other lying in the XY and YZ plane. Find the magnitude and direction of the net magnetic field at the centre of the coils.
View SolutionA straight wire carrying a current of 5 A is bent into a semicircular arc of radius 2 cm as shown in the fig. Find the magnitude and direction of the magnetic field at the centre of the arc.

View Solution

