Four particles, each of mass $M$ , move along a circle of radius $R$ under the acting of their mutual graviational attraction. The speed of each particle is

A

$\frac{G M}{R}$

B

$\sqrt{2 \sqrt{2} \frac{G M}{R}}$

C

$\sqrt{\frac{G M}{R} (2 \sqrt{2} + 1)}$

D

$\sqrt{\frac{G M}{R} (\frac{2 \sqrt{2} + 1}{4})}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

Side of square : $r = 2 R {cos 45}^{\circ} = \sqrt{2} R$

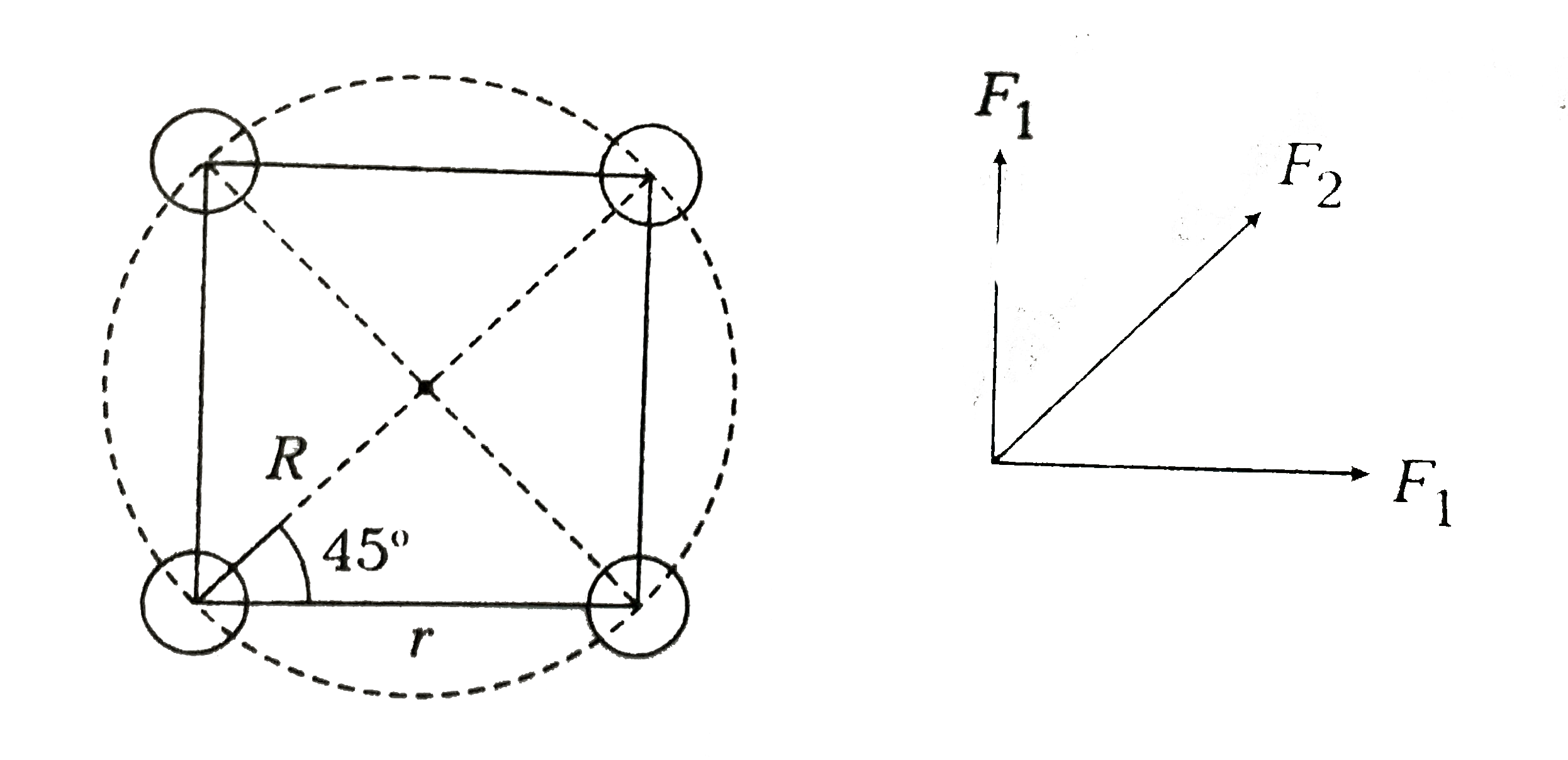
Now, $2 F_{1} {cos 45}^{\circ} + F_{2} = \frac{M v^{2}}{R}$
$\Rightarrow v = \sqrt{\frac{R}{M} (\sqrt{2} F_{1} + F_{2})}$
$\Rightarrow v = \sqrt{\frac{R}{M} ⎡ ⎢ ⎢ ⎢ ⎣ \sqrt{2} \frac{G M . M}{{(\sqrt{2} R)}^{2}} + \frac{G M M}{{(2 R)}^{2}} ⎤ ⎥ ⎥ ⎥ ⎦}$
$= \sqrt{\frac{G M}{R} (\frac{2 \sqrt{2 + 1}}{4})}$ .

Updated on:21/07/2023

|

Class 11 PHYSICS GRAVITATION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A $\frac{1}{2 R} \sqrt{(\frac{1}{G m})}$
B $\sqrt{(\frac{G m}{2 R})}$
C $\frac{1}{2} \sqrt{(\frac{G m}{R})}$
D $\sqrt{(\frac{4 G m}{R})}$

DC PANDEY ENGLISH-GRAVITATION-(A) Chapter Exercises

Home
Ask Doubt
Profile