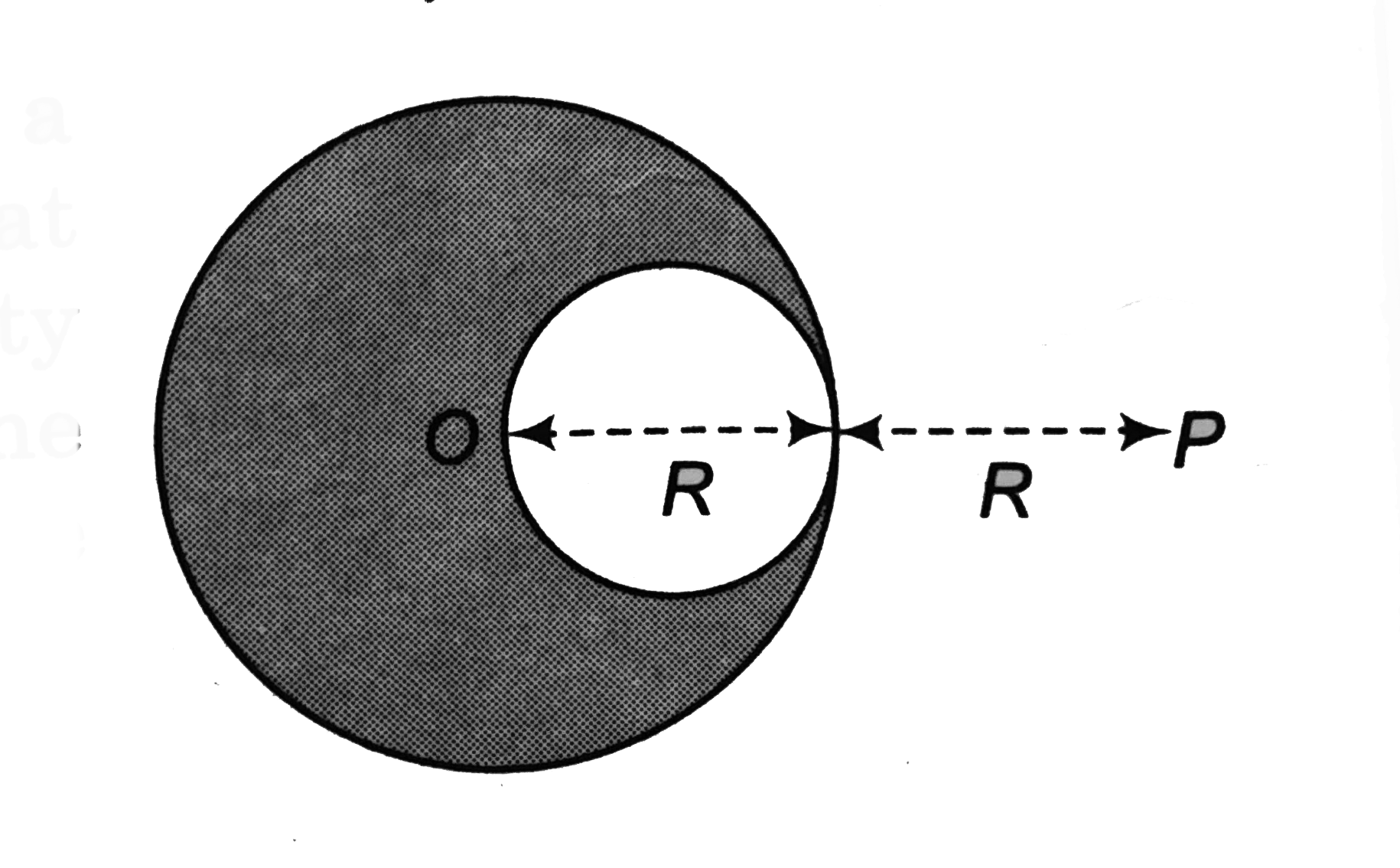
A solid sphere of uniform density and radius R applies a gravitational force of attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shown in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be
59
78
34
79
The correct Answer is:D
F1=GMm(2R)2=GMm4R2
F2=F1−Fcavity=GMm4R2−G(M8)(m)(32R)2
⇒F2=7GMn36R2⇒F2F1=79.
Topper's Solved these Questions
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (B) Chapter Exercises
31 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - (C) Chapter Exercises
45 Videos
- GRAVITATIONBOOK - DC PANDEY ENGLISHCHAPTER - GRAVITATIONEXERCISE - Check Point 10.6
20 Videos
- GENERAL PHYSICSBOOK - DC PANDEY ENGLISHCHAPTER - GENERAL PHYSICSEXERCISE - INTEGER_TYPE
2 Videos
- KINEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - KINEMATICSEXERCISE - INTEGER_TYPE
10 Videos
Similar Questions
A solid sphere of uniform density and radius R applies a gravitational force attraction equal to F1 on a particle placed at P, distance 2R from the centre O of the sphere. A spherical cavity of radius R/2 is now made in the sphere as shows in figure. The particle with cavity now applies a gravitational force F2 on same particle placed at P. The radio F2/F1 will be

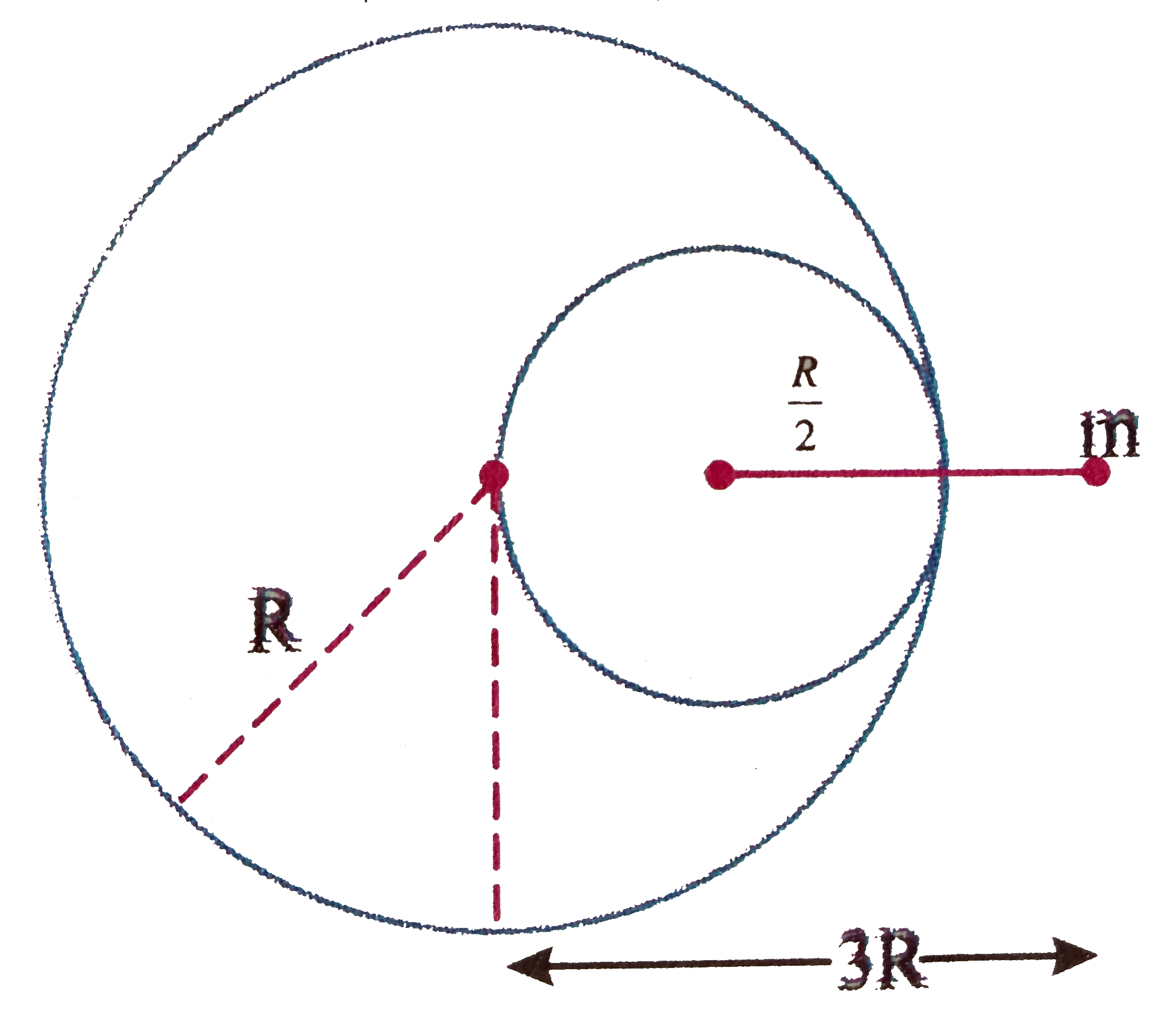
View SolutionThe gravitational force acting on a particle, due to a solid sphere of uniform density and radius R, at a distance of 3R from the centre of the sphere is F1. A spherical hole of radius (R/2) is now made in the sphere as shown in diagram. The sphere with hole now exerts a force F2 on the same particle. ratio of F1 to F2 is
View SolutionA hemi-spherical cavity is created in solid sphere (of radius 2R) as shown in the figure. Then

View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA hemispherical cavity of radius R is created in a solid sphere of radius 2R as shown in the figure . They y -coordinate of the centre of mass of the remaining sphere is

View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distance R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA solid sphere of mass M and radius R has a spherical cavity of radius R/2 such that the centre of cavity is at a distance R/2 from the centre of the sphere. A point mass m is placed inside the cavity at a distanace R/4 from the centre of sphere. The gravitational force on mass m is
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.

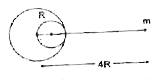
View SolutionA particle of mass m is placed at a distance of 4R from the centre of a huge uniform sphere of mass M and radius R. A spherical cavity of diameter R is made in the sphere as shown in the figure. If the gravitational interaction potential energy of the system of mass m and the remaining sphere after making the cavity is λGMm28R. Find the value of λ
View SolutionA uniform ring of mas m and radius a is placed directly above a uniform sphere of mass M and of equal radius. The centre of the ring is at a distance √3 a from the centre of the sphere. Find the gravitational force exerted by the sphere on the ring.
View Solution
