Four particles each of mass 'm' are placed at the four vertices of a square 'a' .Find net force on any one the particle.
The correct Answer is:A, B
To find the net gravitational force acting on one of the particles located at the vertices of a square, we can follow these steps:
Step 1: Identify the Configuration
Consider a square with vertices labeled A, B, C, and D, where each vertex has a particle of mass m. We will calculate the net force acting on particle D due to particles A, B, and C.
Step 2: Calculate Forces Due to Each Particle
1. Force on D due to A (F_DA):
- The distance between particles D and A is equal to the side of the square, a.
- The gravitational force is given by:
FDA=Gm2a2
2. Force on D due to B (F_DB):
- The distance between particles D and B is also equal to the side of the square, a.
- The gravitational force is:
FDB=Gm2a2
3. Force on D due to C (F_DC):
- The distance between particles D and C is the diagonal of the square, which can be calculated using the Pythagorean theorem:
Distance=√a2+a2=a√2
- The gravitational force is:
FDC=Gm2(a√2)2=Gm22a2
Step 3: Resolve Forces into Components
Next, we need to resolve the forces FDA, FDB, and FDC into their x and y components.
1. Components of F_DA:
- FDA,x=FDA⋅cos(45∘)=Gm2a2⋅1√2=Gm2a2√2
- FDA,y=FDA⋅sin(45∘)=Gm2a2⋅1√2=Gm2a2√2
2. Components of F_DB:
- FDB,x=0 (since it acts vertically downwards)
- FDB,y=−FDB=−Gm2a2
3. Components of F_DC:
- FDC,x=−FDC⋅cos(45∘)=−Gm22a2⋅1√2=−Gm22a2√2
- FDC,y=−FDC⋅sin(45∘)=−Gm22a2⋅1√2=−Gm22a2√2
Step 4: Sum the Components
Now, we sum the x and y components to find the net force components acting on particle D.
1. Net Force in the x-direction (F_net,x):
Fnet,x=FDA,x+FDB,x+FDC,x=Gm2a2√2+0−Gm22a2√2=Gm2a2√2−Gm22a2√2=Gm22a2√2
2. Net Force in the y-direction (F_net,y):
Fnet,y=FDA,y+FDB,y+FDC,y=Gm2a2√2−Gm2a2−Gm22a2√2
=Gm2a2√2−Gm2√22a2√2=Gm2a2√2−Gm22a2=Gm22a2√2
Step 5: Calculate the Magnitude of the Net Force
Finally, we can calculate the magnitude of the net force using the Pythagorean theorem:
Fnet=√(Fnet,x)2+(Fnet,y)2
=
⎷(Gm22a2√2)2+(Gm22a2√2)2
=
⎷2(Gm22a2√2)2=Gm22a2√2√2=Gm22a2
Final Result
Thus, the net force acting on any one of the particles is:
Fnet=Gm22a2
Consider a square with vertices labeled A, B, C, and D, where each vertex has a particle of mass m. We will calculate the net force acting on particle D due to particles A, B, and C.
1. Force on D due to A (F_DA):
- The distance between particles D and A is equal to the side of the square, a.
- The gravitational force is given by:
FDA=Gm2a2
- The distance between particles D and B is also equal to the side of the square, a.
- The gravitational force is:
FDB=Gm2a2
- The distance between particles D and C is the diagonal of the square, which can be calculated using the Pythagorean theorem:
Distance=√a2+a2=a√2
- The gravitational force is:
FDC=Gm2(a√2)2=Gm22a2
Next, we need to resolve the forces FDA, FDB, and FDC into their x and y components.
- FDA,x=FDA⋅cos(45∘)=Gm2a2⋅1√2=Gm2a2√2
- FDA,y=FDA⋅sin(45∘)=Gm2a2⋅1√2=Gm2a2√2
- FDB,x=0 (since it acts vertically downwards)
- FDB,y=−FDB=−Gm2a2
- FDC,x=−FDC⋅cos(45∘)=−Gm22a2⋅1√2=−Gm22a2√2
- FDC,y=−FDC⋅sin(45∘)=−Gm22a2⋅1√2=−Gm22a2√2
Now, we sum the x and y components to find the net force components acting on particle D.
Fnet,x=FDA,x+FDB,x+FDC,x=Gm2a2√2+0−Gm22a2√2=Gm2a2√2−Gm22a2√2=Gm22a2√2
Fnet,y=FDA,y+FDB,y+FDC,y=Gm2a2√2−Gm2a2−Gm22a2√2
=Gm2a2√2−Gm2√22a2√2=Gm2a2√2−Gm22a2=Gm22a2√2
Finally, we can calculate the magnitude of the net force using the Pythagorean theorem:
Fnet=√(Fnet,x)2+(Fnet,y)2
=
⎷(Gm22a2√2)2+(Gm22a2√2)2
=
⎷2(Gm22a2√2)2=Gm22a2√2√2=Gm22a2
Thus, the net force acting on any one of the particles is:
Fnet=Gm22a2
Topper's Solved these Questions
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Solved Examples
Explore 16 Videos
- GRAVITATIONBook:DC PANDEY ENGLISHChapter:GRAVITATIONExercise:Miscellaneous Examples
Explore 8 Videos
- GENERAL PHYSICSBook:DC PANDEY ENGLISHChapter:GENERAL PHYSICSExercise:INTEGER_TYPE
Explore 2 Videos
- KINEMATICSBook:DC PANDEY ENGLISHChapter:KINEMATICSExercise:INTEGER_TYPE
Explore 10 Videos
Similar Questions
Four particles each of mass m are kept at the four vertices of a square of side 'a' . Find gravitational potential energy of this system.
View SolutionFour particles each of mass 'm' are kept at the four corners of a square of edge 'a'. Find the moment of inertia of the system about a line perpendicular to the plane of the square and passing through the center of the square.
View Solution
Knowledge Check
Four particles each of mass m are placed at the vertices of a square of side l. the potential at the centre of square is
A−√2Gm2l(2−1√2)B−2Gm2l(2+1√2)C−√2Gm2l(√2−1√2)D−2Gm2l(√2−1√2)
Four identical particles each of mass m are arranged at the corners of a square of sie a. If mass of one of th particle is doubled, the shift in the centre of mass of the system is
View SolutionFour bodies each of mass m are placed at the different corners of a square of side a. find the work done on the system to take any one body to infinity.
View SolutionFind the gravitational potential energy of a system of four particles, each of mass m placed at the verticles of a square of side l. Also obtain the gravitaitonal potential at centre of the square.
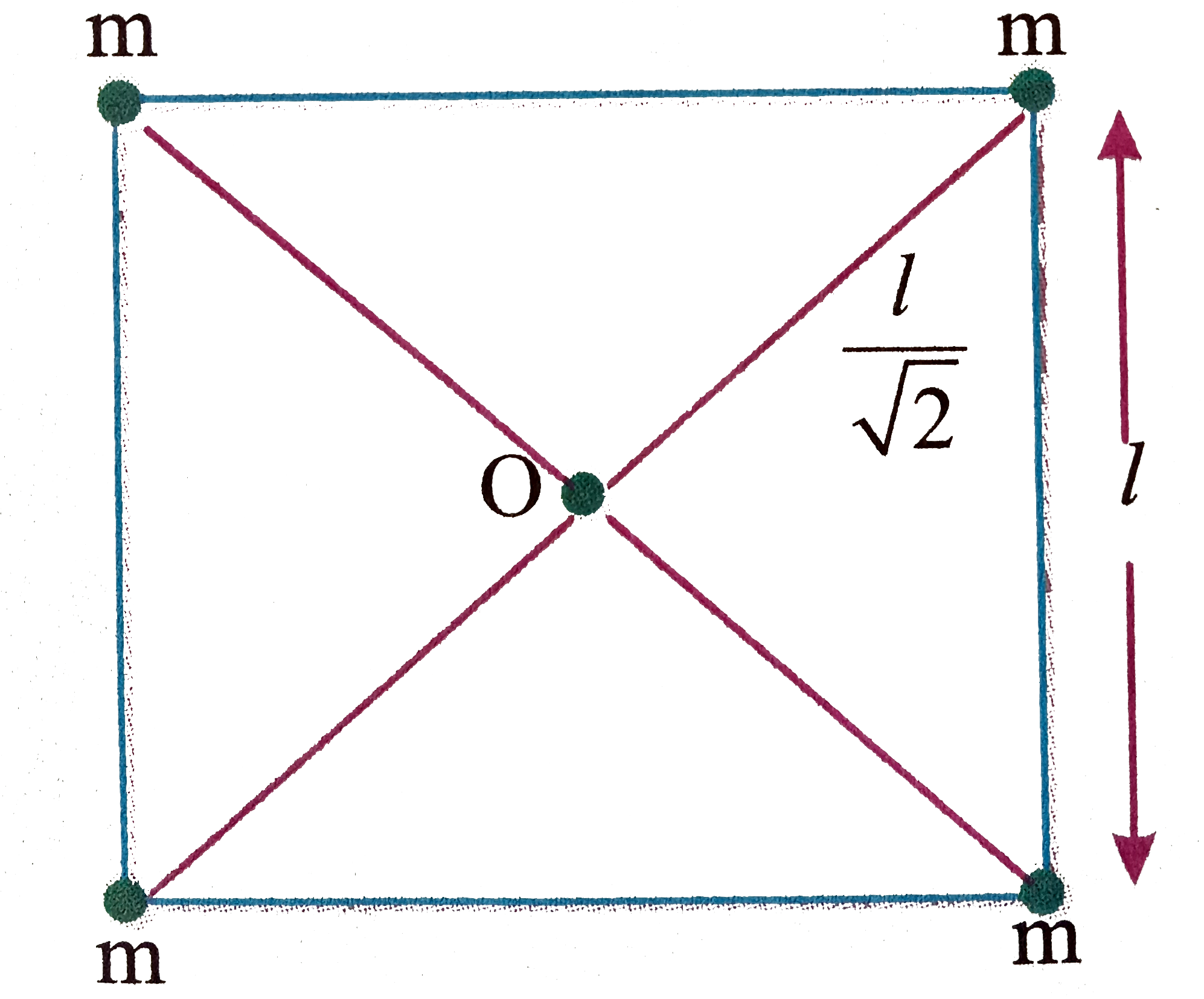
View SolutionFour particles each of mass 'm' are located at the four corners of a sqaure of side a. If the system is revolving in a circle due to thei mutual force of attraction then the angular velocity and time period of each particle is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionFour identical particles each of mass 1 kg are arranged at the corners of a square of side length 2√2m. If one of the particles is removed, the shift in the centre of mass is
View SolutionThree identical particles each of mass m are placed at the vertices of an equilateral triangle of side a. Fing the force exerted by this system on a particle P of mass m placed at the
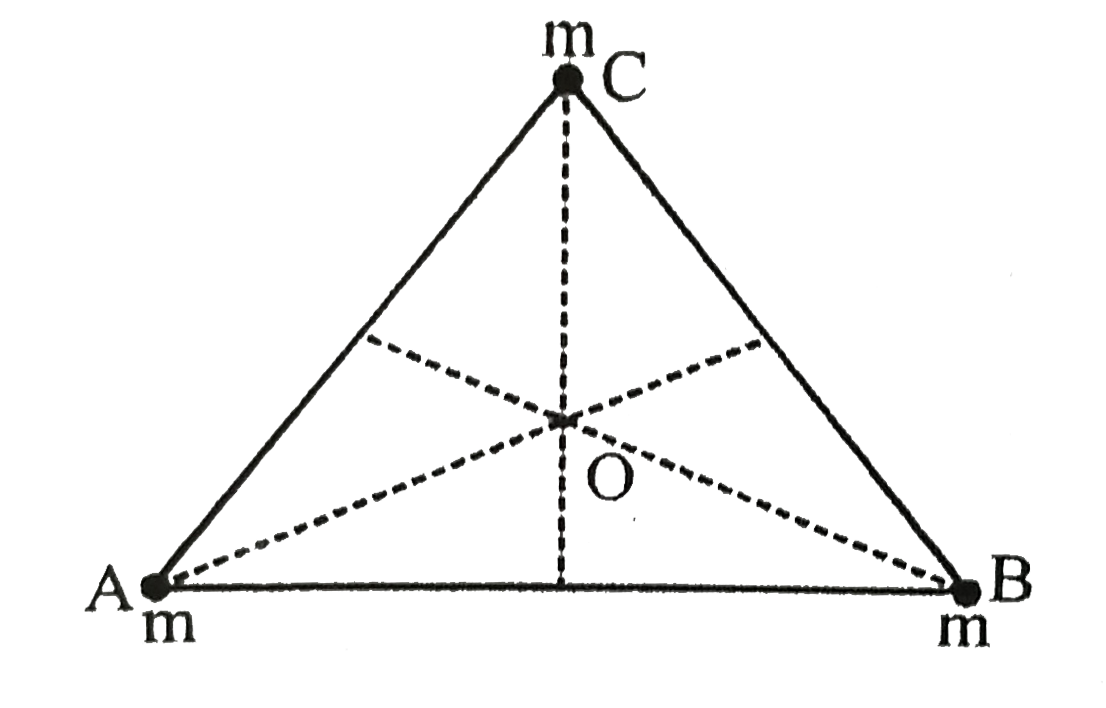
(a) the mid point of a side
(b) centre of the triangle
View Solution

