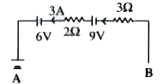Consider
 .
.
The condition for which the potential difference between A and B is zero is.
A
C1C2=C3C4
B
C1C4=C2C3
C
C1C3=C2C4
D
none of these
Video Solution
Text Solution
The correct Answer is:B
Let charge be as shown. (Capacitors in series have the same the charge.)
Taking loop containing C1,C2, and E, we get
qC1+qC2−E=0 or q=E[C1C2C1+C2]
Similarly, from loop containing C3,C4, and E, we get
q'C3+q'C4−E=0 or q'=E[C3C4C3+C4]
Now, VA−VB=qC2−q'C
=E[C1C1+C2−C3C3+C4]
=E[C1C4−C3C2(C1+C2)(C3+C4)]
Now VA−VB=E⇒C1C4−C2C3=0
or C1C2=C3V4.
|
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Integer
Explore 5 Videos
- CAPACITOR AND CAPACITANCEBook:CENGAGE PHYSICS ENGLISHChapter:CAPACITOR AND CAPACITANCEExercise:Multile Correct
Explore 11 Videos
- ATOMIC PHYSICSBook:CENGAGE PHYSICS ENGLISHChapter:ATOMIC PHYSICSExercise:ddp.4.3
Explore 15 Videos
- CENGAGE PHYSICS DPPBook:CENGAGE PHYSICS ENGLISHChapter:CENGAGE PHYSICS DPPExercise:subjective type
Explore 51 Videos
Similar Questions
Knowledge Check
The potential difference between A and B as shown in figure is
 A1VB2VC3VD4V
A1VB2VC3VD4V
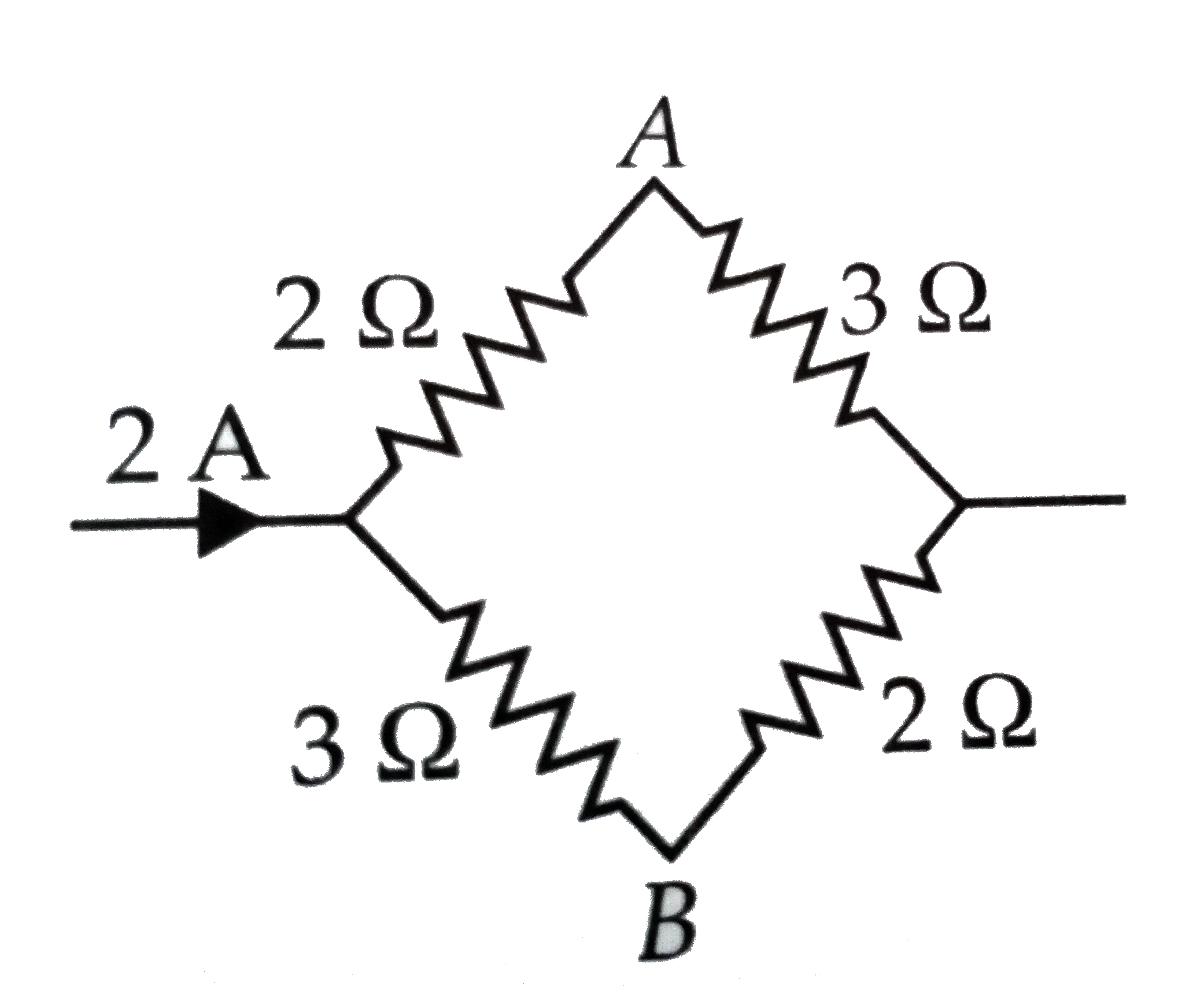
The potential difference between points A and B is
View SolutionThe potential difference between points A and B is

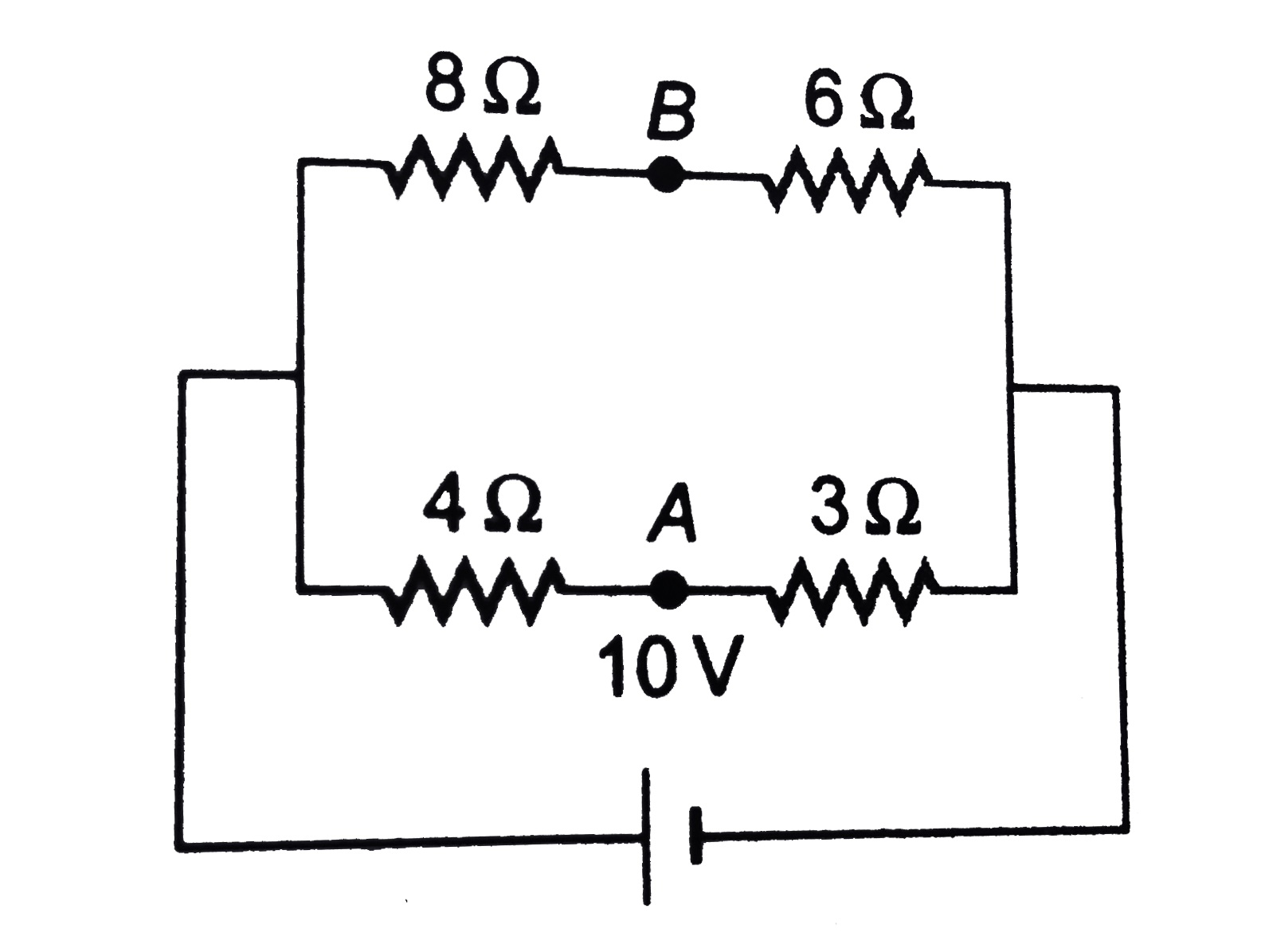
View SolutionIn the figure potential difference between A and B is :

View SolutionIn the circuit below, the potential difference between A and B is

View SolutionIn the figure, potential difference between A & B is
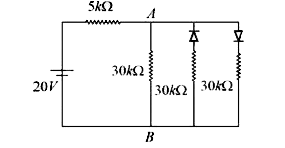
View SolutionIn the figure, potential difference between A & B is
View SolutionIn the figure, potential difference between A & B is

View Solution