In each capacitance C1is6.0μF, and each capacitance C2 is 4.0μF.
 .
.
With 420V across a and b the value of Vc−Vd is.
24.6V
46.7V
18V
72V
The correct Answer is:B
Reduction of the farthest right leg yields
C=(16.0μF+16.0μF+16.0μF)−1=20.0μF=C13
It combines in parallel with C2,i.e.,
C=4.0μF+2.0μF=6.0μF=C1
So the next reduction is the same as the second, leaving 3C1's, in series.
So Ceq=2.0μF=C1/3. For the three capacitors nearest to points a and b:
QC1=CeqV=(2.0×10−6F)(420V)=8.4×10−4C
Vcd=13(4203V)=46.7V.
By symmetry, the total voltage drop over the equivalent capacitance of the part of the circuit from the junctions betweenc and d is (420/3)V and the equivalent capacitance is that of one of those capacitors, i.e., 1/3 of 420/3V.
Topper's Solved these Questions
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Integer
5 Videos
- CAPACITOR AND CAPACITANCEBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CAPACITOR AND CAPACITANCEEXERCISE - Multile Correct
11 Videos
- ATOMIC PHYSICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ATOMIC PHYSICSEXERCISE - ddp.4.3
15 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
Similar Questions
In each capacitance C1 is 6.0μF, and each capacitance C2 is 4.0μF.
 .
.
The charge on C1 nearest to a when Vab=420V is.
View SolutionIn each capacitance C1 is 6.0μF, and each capacitance C2 is 4.0μF.
 .
.
The equivalent capacitance of the netwok between ponts a and b is.
View SolutionEach capacitance shown in is in μF. Find the charge on 6μF.
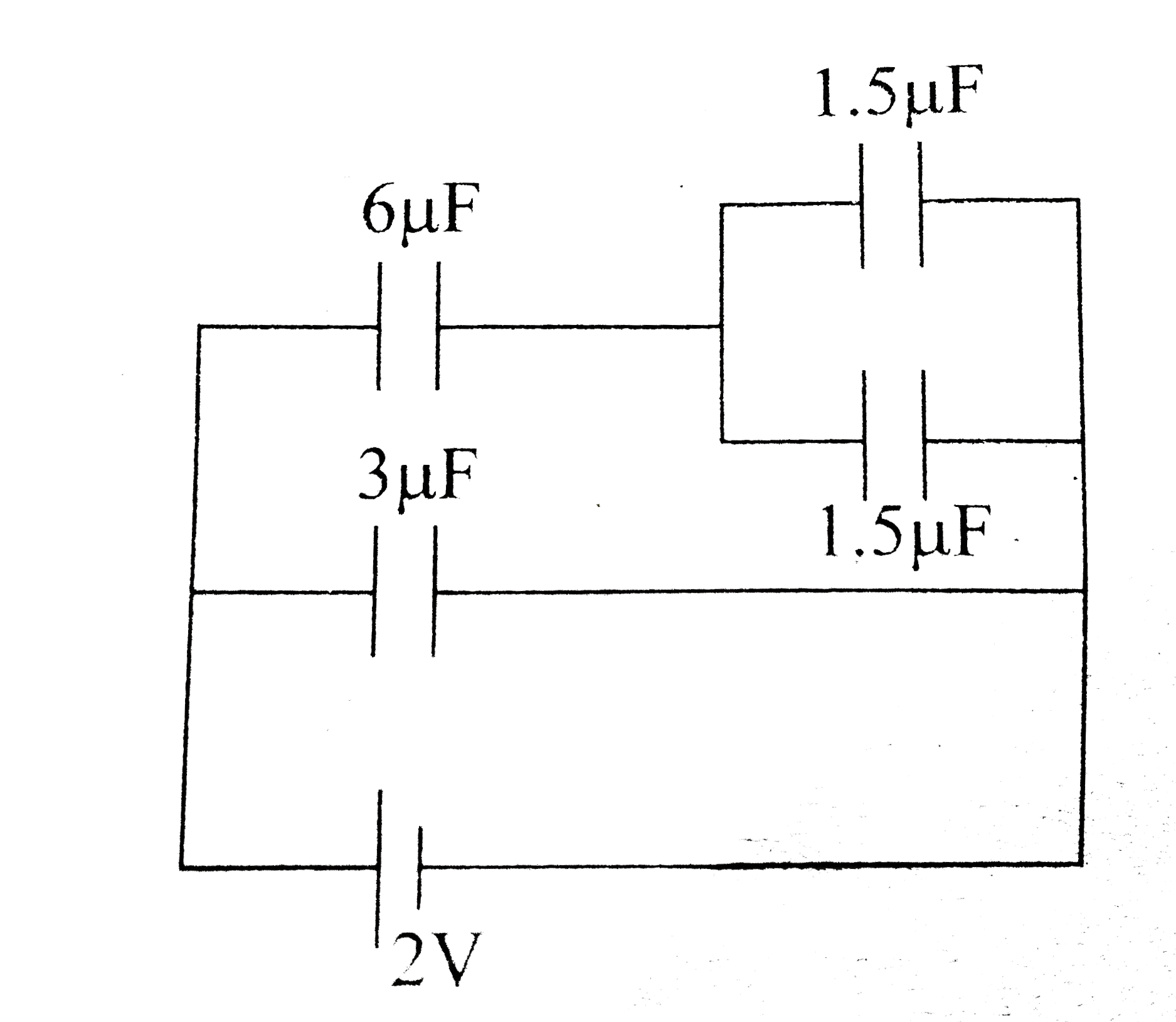 .
.
View SolutionA capacitor of capacitance C1=1μF withstand a maximum voltage of V1=6KV, and another capacitor of capacitance C2=2μF, can with stand a maximum voltage of V2=4KV. If they are connected in series, what maximum voltage will the system withstand?
View SolutionA capaitor of capacitance C1=1.0μF withstands teh maximum voltage V1=6.0kV while a capacitor of capacitance Cs=2.0μF, the maximum voltage Vs=4.0kV. What voltage will the system of these two capacitors withsatand if they are connected in sereis ?
View SolutionA circuit shown in the figure consists of a battery of emf 10V and two capacitance C1 and C2 of capacitances 1.0μF and 2.0μF respectively. The potential difference VA−VB is 5V
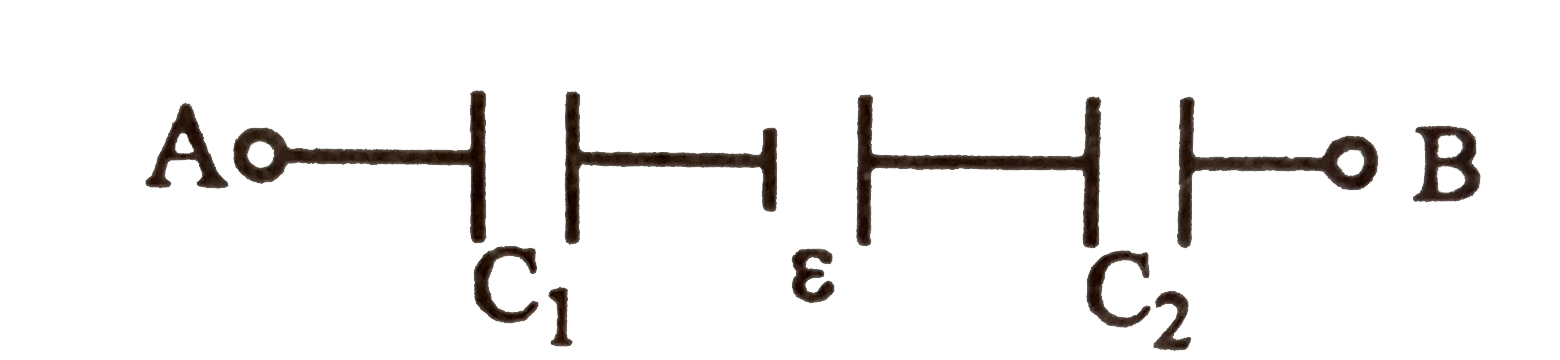
View SolutionIn the given network capacitance, C1=10μF,C2=5μF and C3=4μF. What is the resultant capacitance between A and B?
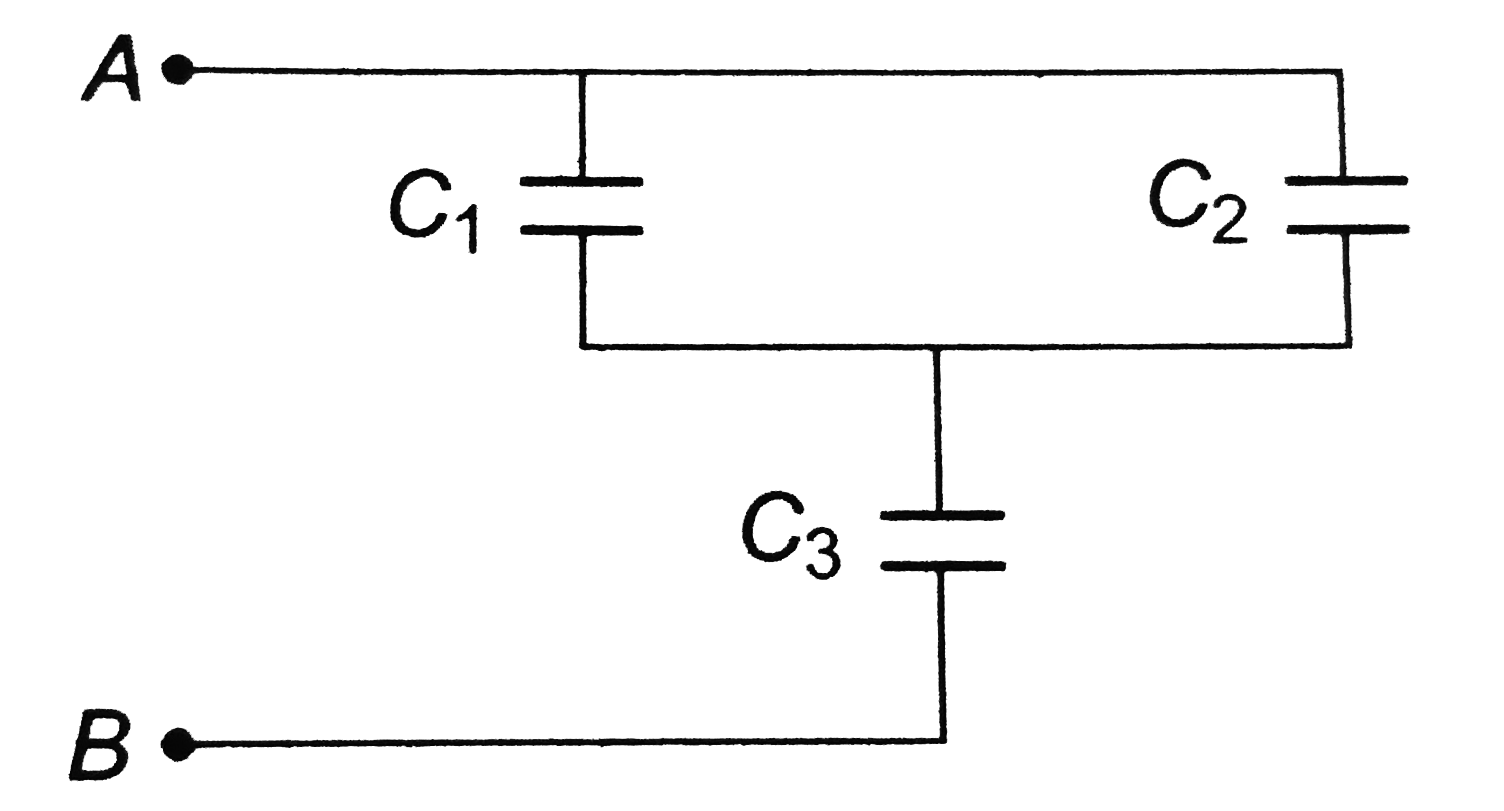
View SolutionIn the given network capacitance, C1=10μF,C2=5μF and C3=4μF. What is the resultant capacitance between A and B?

View SolutionA circuit has section AB as shown in The emf of the cell is 10V, and the capacitors have capacitances C1=1μF and C2=2μF. Find the voltage across each capacitor.
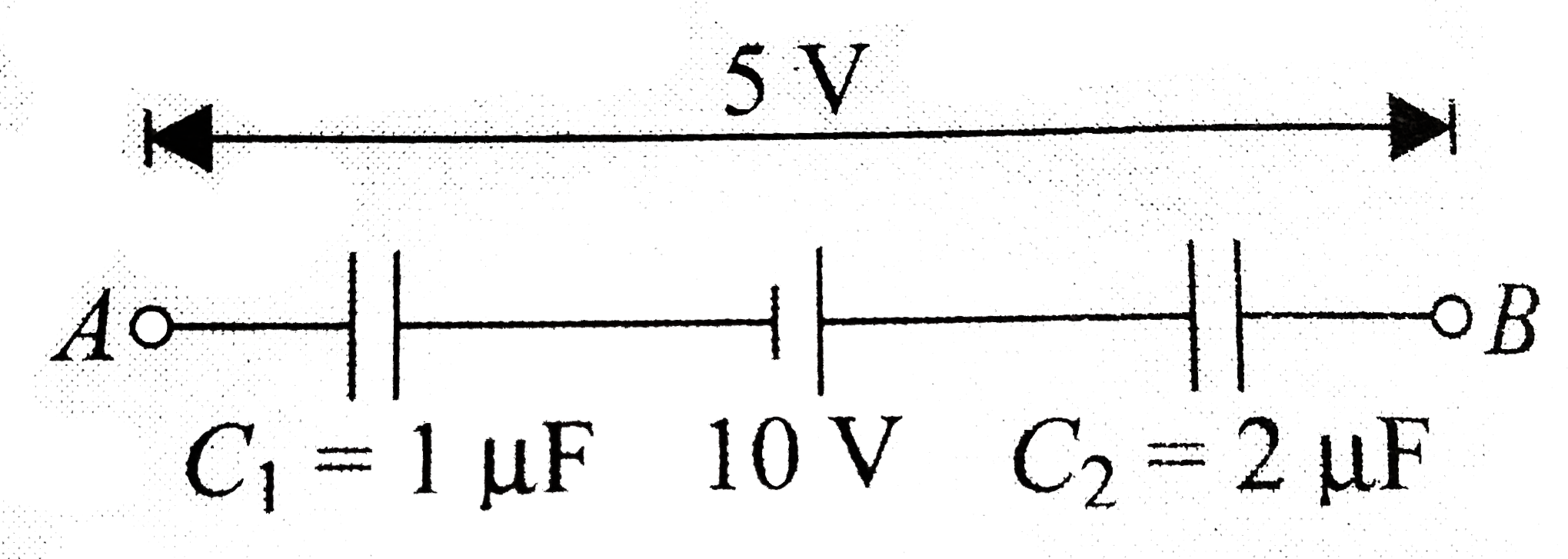 .
.
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View Solution
