Calculate potential energy of a point charge −q placed along the axis due to a charge +Q uniformly distributed along a ring of radius R. Sketch P.E. as a function of a axial distance z from the center of the ring, Looking at graph, can you see what happen if −q is displaced slightly from the centre of the ring (along the axis) ?
Here a ring of radius R is given, on whose circumference +Q charge is distributed uniformly.
Let us consider a charge -q kept at a point P on the axis of the ring. Let the distance between the point P and centre of the ring be z.
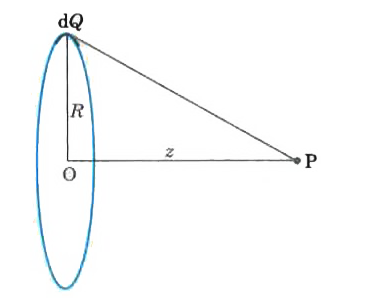
Consider a segment of charge dQ on the ring.
Electric potential due to this segment on point P can be written as follows:
dV=14πε0dQ√R2+z2
We can integrate it for the complete ring to get total potential at point P.
V=∫Ring14πε0Q√R2+z2
Except dQ, everything else is constant and can be taken out of the integration and the integration of dQ is total charge on the ring.
⇒V=14πε01√R2+z2∫RingdQ
⇒V=14πε0Q√R2+z2
All points on circumference of the ring are equidistant from any point on its axis. Hence, the above result is also predictable without any calculation.
Potential energy of point charge -q kept at point P can be calculated as:
U=−qV
⇒U=14πε0−dQ√R2+z2
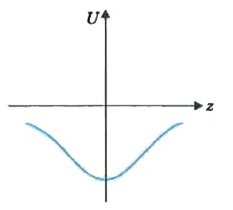
Potential energy at any point on the axis, z distance away from the centre will vary as shown in the figure.
When charge -q is displaced slightly from the centre charge -q is displaced slightly from the centre of the ring along the axis, the charge will perform oscillations. A point of minimum potential energy is supposed to the point of stable equilibrium. The particle will oscillate about a stable equilibrium position, which is the centre of the ring in this case.
Note that if the given point charge were positive, then the above graph would be just vertically inverted (or mirror image about Z-axis of graph). Thus, there will be maximum potential energy at the centre and it would be the point of unstable equilibrium. Also, the positive charge cannot oscillate.
Related Playlists
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Higher Order Thinking Skills & Advanced Level (QUESTIONS WITH ANSWERS)10videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - Revision Exercises (Very Short Answer Questions)56videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - NCERT FILE Solved (Exemplar Problems) (Very Short Answer Type Questions)5videos
ELECTROSTATIC POTENTIAL AND CAPACITANCE
- BOOK - MODERN PUBLICATIONCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - CHAPTER PRACTICE TEST14videos
ELECTROMAGNETIC WAVES
- BOOK - MODERN PUBLICATIONCHAPTER - MAGNETISM AND MATTEREXERCISE - CHAPTER PRACTICE TEST FOR BOARD EXAMINATION16videos
MAGNETISM AND MATTER
Similar Practice Problems
- Question 1 - Select One
A charge of 5 nC is uniformly distributed on a ring of radius 4 cm. Find the potential at the axis at a distance of 3 cm from the center.
A0.09VB600 VC900 VD300 V - Question 1 - Select One
A positive charge Q is uniformly distrubuted along a circular ring of radius R.a small test chage q is placed at the centre of the ring .The
 Aif q>0 and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.Bif q<0 and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.Cif q<0 it will perform SHM for small displacement along the axisDq at the centre of the ring is in an unstable equilibrium within the plane of the ring for q<0
Aif q>0 and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.Bif q<0 and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.Cif q<0 it will perform SHM for small displacement along the axisDq at the centre of the ring is in an unstable equilibrium within the plane of the ring for q<0 - Question 1 - Select One
Charges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2 - Question 1 - Select One
A charge Q is uniformly distributed only on the fourths portion of a ring of radius R. The elctric potential at centre of ring is
A3Q4πε0RBQ4πε0RC3Q2πε0RD6Q4πε0R
Similar Questions
Calculate potential energy of a point charge −q placed along the axis due to a charge +Q uniformly distributed along a ring of radius R. Skecth P.E. as a function of a axial distance z from the center of the ring, Looking at graph, can you see what happen if −q is displaced slighlty from the centre of the ring (along the axis) ?
View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of readius R.
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .
 View Solution
View SolutionCalculate potential on the axis of a disc of radius R due to a charge Q uniformly distributed on its surface.
View SolutionA charge Q is uniformly on a ring of radius R. Find the electric potential on the axis of ring at distance x from the centre of the ring. Sketch variation of potential with respect to x.
View SolutionPotential on the axis of ring of radius 3R and at distance 4R from centre of ring is (charge on the ring is Q )
View Solution

