Calculate potential energy of a point charge $- q$ placed along the axis due to a charge $+ Q$ uniformly distributed along a ring of radius R. Sketch P.E. as a function of a axial distance z from the center of the ring, Looking at graph, can you see what happen if $- q$ is displaced slightly from the centre of the ring (along the axis) ?

Video Solution

Text Solution

Verified by Experts

Here a ring of radius R is given, on whose circumference +Q charge is distributed uniformly.
Let us consider a charge -q kept at a point P on the axis of the ring. Let the distance between the point P and centre of the ring be z.

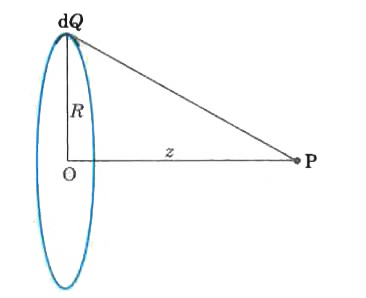
Consider a segment of charge dQ on the ring.
Electric potential due to this segment on point P can be written as follows:
$d V = \frac{1}{4 π ε_{0}} \frac{d Q}{\sqrt{R^{2} + z^{2}}}$
We can integrate it for the complete ring to get total potential at point P.
$V = \int Ring \frac{1}{4 π ε_{0}} \frac{Q}{\sqrt{R^{2} + z^{2}}}$
Except dQ, everything else is constant and can be taken out of the integration and the integration of dQ is total charge on the ring.
$\Rightarrow V = \frac{1}{4 π ε_{0}} \frac{1}{\sqrt{R^{2} + z^{2}}} \int Ring d Q$
$\Rightarrow V = \frac{1}{4 π ε_{0}} \frac{Q}{\sqrt{R^{2} + z^{2}}}$
All points on circumference of the ring are equidistant from any point on its axis. Hence, the above result is also predictable without any calculation.
Potential energy of point charge -q kept at point P can be calculated as:
$U = - q V$
$\Rightarrow U = \frac{1}{4 π ε_{0}} \frac{- d Q}{\sqrt{R^{2} + z^{2}}}$

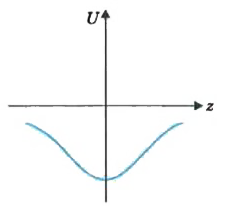
Potential energy at any point on the axis, z distance away from the centre will vary as shown in the figure.
When charge -q is displaced slightly from the centre charge -q is displaced slightly from the centre of the ring along the axis, the charge will perform oscillations. A point of minimum potential energy is supposed to the point of stable equilibrium. The particle will oscillate about a stable equilibrium position, which is the centre of the ring in this case.
Note that if the given point charge were positive, then the above graph would be just vertically inverted (or mirror image about Z-axis of graph). Thus, there will be maximum potential energy at the centre and it would be the point of unstable equilibrium. Also, the positive charge cannot oscillate.

Updated on:21/07/2023

A charge of 5 nC is uniformly distributed on a ring of radius 4 cm. Find the potential at the axis at a distance of 3 cm from the center.
A $0.09 V$
B600 V
C900 V
D300 V
A positive charge $Q$ is uniformly distrubuted along a circular ring of radius $R$ .a small test chage $q$ is placed at the centre of the ring .The

Aif $q > 0$ and is displaced away from the centre in the plane of the ring.it will be pushed back towards the centre.
Bif $q < 0$ and is displaced away from the cnetre in the plane of the ring .it will never return to the centre and will continue moving till it hits the ring.
Cif $q < 0$ it will perform $S H M$ for small displacement along the axis
D $q$ at the centre of the ring is in an unstable equilibrium within the plane of the ring for $q < 0$
Charges $q$ is uniformly distributed over a thin half ring of radius $R$ . The electric field at the centre of the ring is
A $\frac{q}{2 π^{2} ε_{0} R^{2}}$
B $\frac{q}{4 π^{2} ε_{0} R^{2}}$
C $\frac{q}{4 π ε_{0} R^{2}}$
D $\frac{q}{2 π ε_{0} R^{2}}$