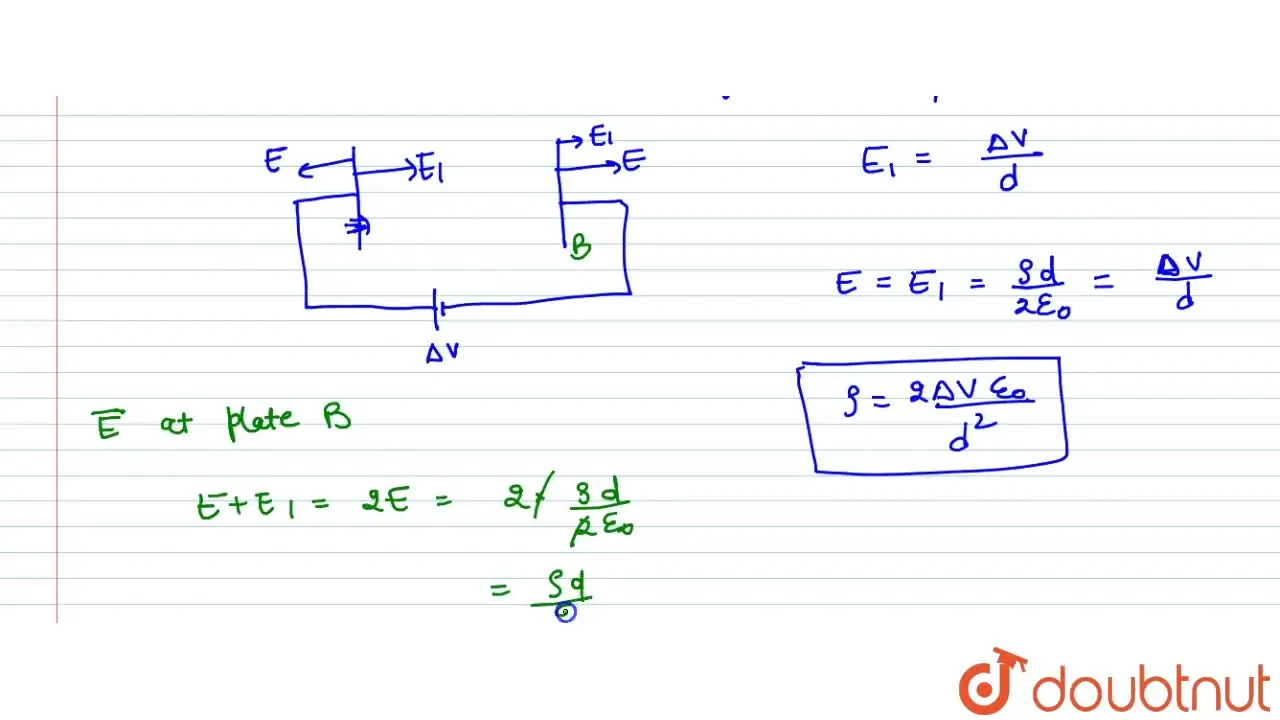
A uniformly distributed space charge fills up the space between two large parallel plates separated by a distance d. The potential difference between the plates is equal to zero ? What will then be the field strength near the other plate ?
In the space between the plates we have the Poission equation
∂2φ∂x2=−ρ0ε0
or, φ=−ρ02ε0x2+Ax+B
where ρ0 is the constant space charge density between the plates.
We can choose φ(0)=0 so B=0
Then φ(d)=Δφ=Ad−ρ0d22ε0 or, A=Δφd+ρ0d2ε0
Now E=∂φ∂x=ρ0ε0x−A=0 for x=0
if A=Δφd+ρ0d2ε0=0
then ρ0=−2ε0Δφd2
E(d)=ρ0dε0
Related Playlists
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Conductors And Dielectrics In An Electric Field47videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRODYNAMICSEXERCISE - Electric Capacitance - Energy Of An Electric Field46videos
ELECTRODYNAMICS
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTRICITY AND MAGNETISMEXERCISE - All Questions6videos
ELECTRICITY AND MAGNETISM
- BOOK - IE IRODOV, LA SENA & SS KROTOVCHAPTER - ELECTROMAGNETISMEXERCISE - All Questions24videos
ELECTROMAGNETISM
Similar Questions
When a metal slab is placed between the charged identical , parallel plates , the potential difference between the plates
View Solution
Magnetic field in space between the plates isView SolutionAn electron having charge e and mass m starts from the lower plate of two metallic plates separated by a distance d. If the potential difference between the plates is V, the time taken by the electron to reach the upper plate is given by
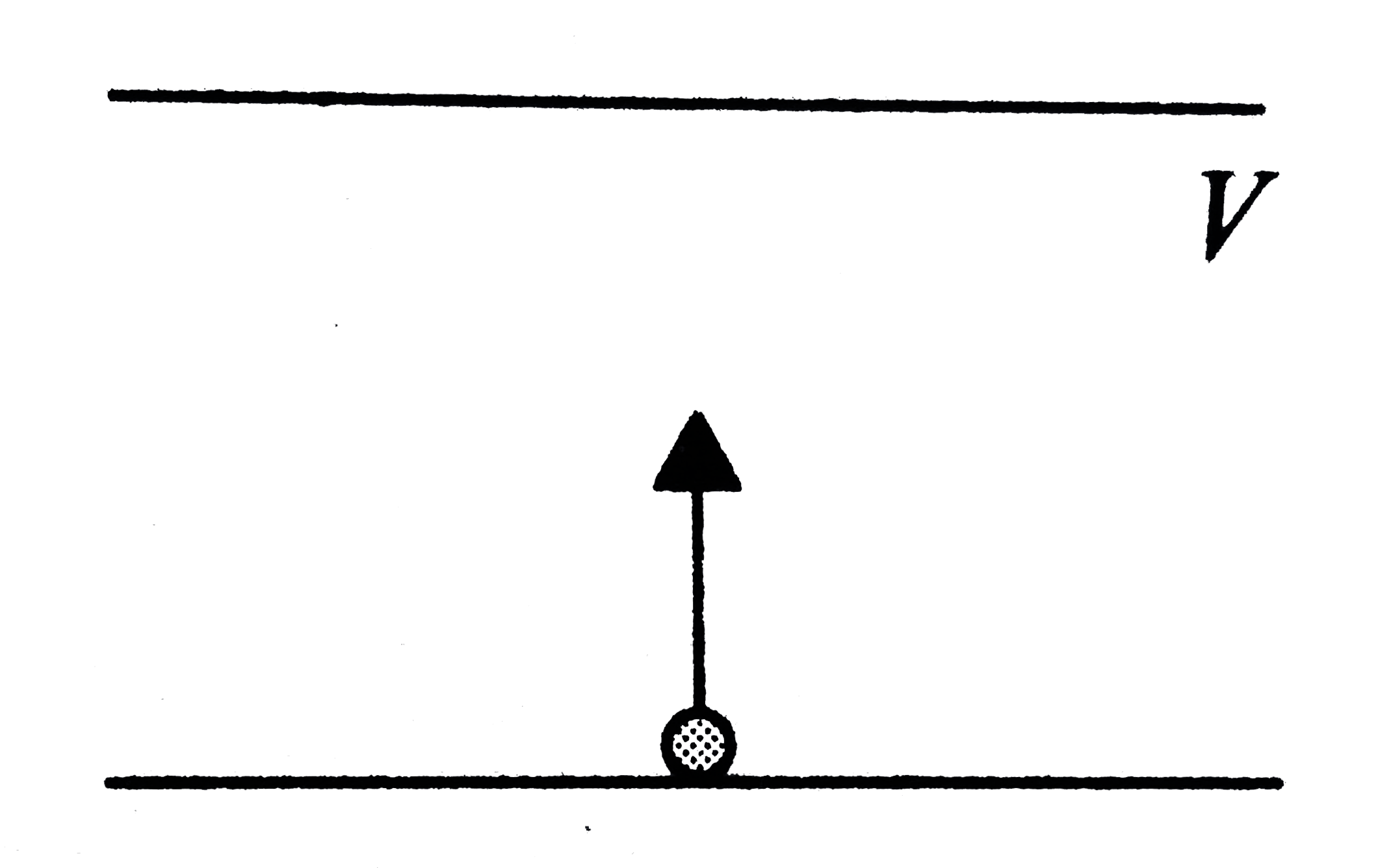 .View Solution
.View SolutionTwo large parallel conducting plates are separated by 40 mm. The potential difference between the plates is V. Potential difference between points X and Y as indicated in the figure will be
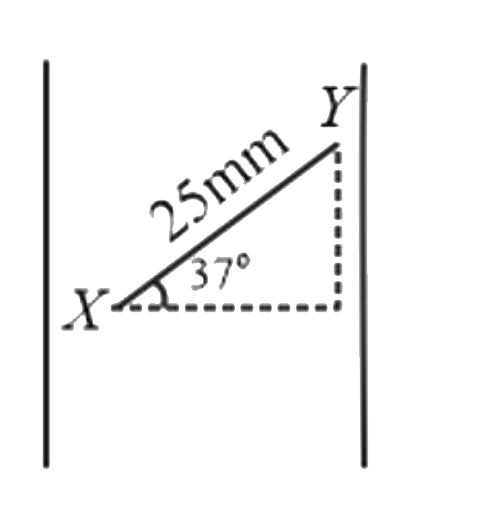 View Solution
View SolutionThe plates of a parallel-plate capacior are given equal positive charges .What will be the potential difference between the plates ? What will be the charges on the facing surfaces and on the outer surfaces ?
View SolutionThe separation between the plates of a charged parallel-plate capacitor is increased. The force between the plates
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionThe distance between the plates of a parallel plate condenser is 4mm and potential difference is 60 volts. If the distance between the plates is increased to 12mm, then
View SolutionThe force between the plates of a parallel plate capacitor of capacitance C and distance of separation of the plates d with a potential difference V between the plates, is.
View SolutionIn a parallel plate capacitor the potential difference of 100 V is manitianed between the plates. If distance between the plates be 5mm, what will be the electric field at points A and B ?
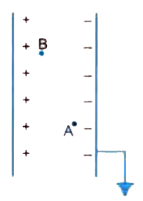 View Solution
View Solution