A proton, a deutron and an alpha particle, after being accelerated through the same potential difference enter a region of uniform magnetic field $\to B$ , in a direction perpendicular to $\to B$ . Find the ratio of their kinetic energies. If the radius of proton's circular path is $7 c m$ , what will be the radii of the paths of deutron and alpha particle?

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $1 : 1 : 2$ , $r_{d} = 7 \sqrt{2} c m$ , $r_{α} = 7 \sqrt{2} c m$

Charge on proton $= e$ , charge on deutron =e,
Charge on $α$ -particle $= 2 e$ .
As $q V = \frac{1}{2} m v^{2} = K$ (kinetic energy)
So, $K \propto q$
$∴ K_{p} : K_{d} : K_{α} = q_{p} : q_{d} : q_{α} = e : e : 2 e$
$= 1 : 1 : 2$
Radius of circular path of a charged particle in a magnetic field is
$r = \frac{m v}{q B} = \frac{\sqrt{2 m K}}{q B}$
( $∵ K = \frac{1}{2} m v^{2}$ or $m v = \sqrt{2 m K}$ )
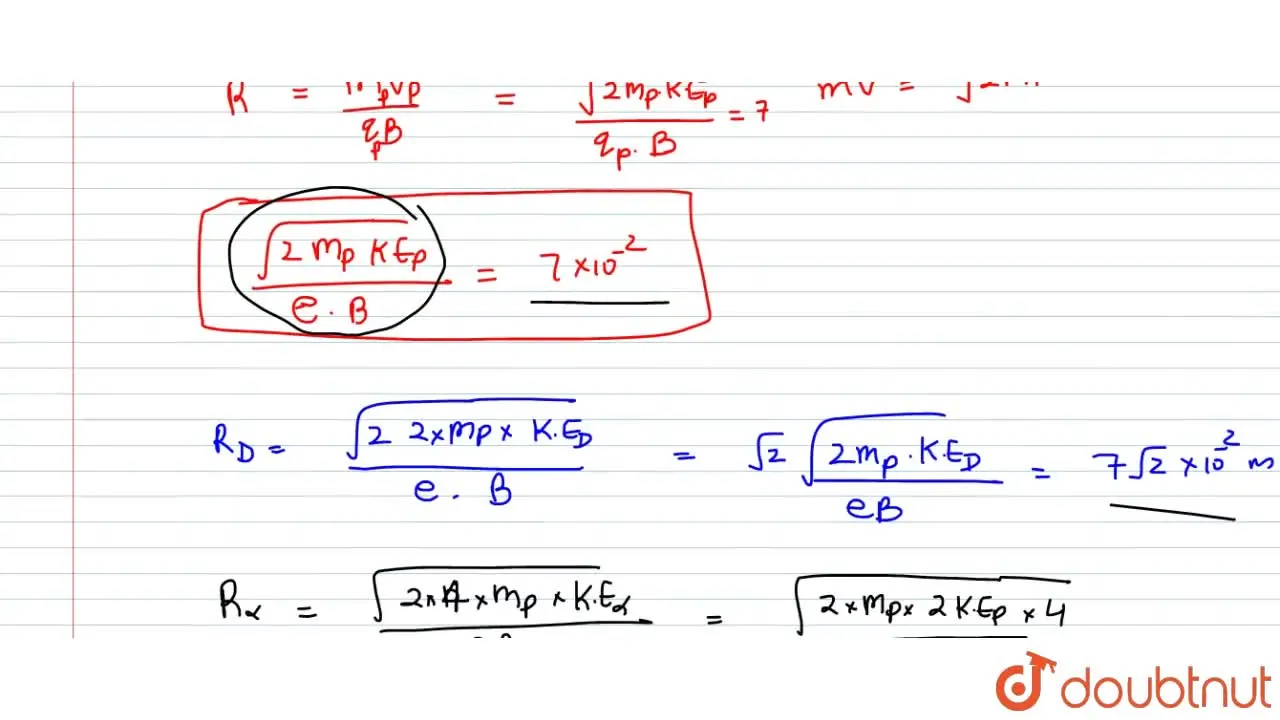
For proton, $r_{p} = \frac{\sqrt{2 m_{p} K_{p}}}{e B} = 7 c m$
For deutron, $r_{d} = \frac{\sqrt{2 m_{d} K_{d}}}{e B}$
$= \sqrt{\frac{2 \times 2 m_{p} \times K_{p}}{e B}} = \sqrt{2} r_{p} = \sqrt{2} \times 7 c m$
For $α$ -particle, $r_{α} = \frac{\sqrt{2 m_{α} K_{α}}}{2 e B}$
$= \sqrt{\frac{2 \times 4 m_{p} \times 2 K_{p}}{2 e B}} = \sqrt{2} r_{p} = \sqrt{2} \times 7 c m$

|

Updated on:21/07/2023

Class 12 PHYSICS MOVING CHARGES AND MAGNETISM

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A proton, a deutron and an $α$ - particle accelerated through the same potential difference enter a region of uniform magnetic field, moving at right angles to it. What is the ratio of their kinetic energy?
A $1 : 1 : 2$
B $2 : 2 : 1$
C $1 : 2 : 1$
D $2 : 1 : 1$
Question 2 - Select One
A proton, a deuteron and an $α$ particle are accelerated through same potential difference and then they enter a normal uniform magnetic field, the ratio of their kinetic energies will be
A $2 : 1 : 3$
B $1 : 1 : 2$
C $1 : 1 : 1$
D $1 : 2 : 4$
Question 3 - Select One
A proton and $α$ particle, after accelerating through same potential difference enters into a uniform magnetic field perpendicular to their velocities, find the radius ratio of proton and $α$ particle:-
A $1 : 2$
B $1 : 1$
C $2 : 1$
D $1 : \sqrt{2}$

PRADEEP-MAGNETIC EFFECT OF CURRENT AND MAGNETISM-Exercise

Home
Ask Doubt
Profile