A masslesss piston divides a closed thermallyy insulated cylinder into two equal parts. One part contains M = 28 g of nitrogen. At this temperature, one-third of molecules are dissociated into atoms and the other part is evacuated. The piston is released and the gas fills the whole volume of the cylinder at temperature T0. Then, the piston is slowly displaced back to its initial position. calculate the increases in internal energy of the gas. Neglect further dissociation of molecules during, the motion of the piston.
Molar mass of N2 gas is M = 28 g
Number of moles of N2, n0=(m/M)=1
One-third molecules are dissociated into atoms.
No. of moles of diatomic N2/2/3
No. of moles of monatomic nitrogen =2×(1/3)
For monatomic gas Cv1=(3/2)R
For diatomic gas Cv2=(5/2)R
Average molar specific heat at constant volume Cv is
n1Cv1+n2Cv2n1p0+n2=(22)(32)R+(23)(52)R23+23=2R
CP−Cv=R⇒CP=3R
γ=CPCV=1.5
Piston is diaplaced bac to its initial position, and during the adiabatic compression, volume of the gas mixture is halved.
For adiabatic compression,
T1Vγ−11=T2Vγ−12
Where T1=T0,V1=V0
T2=?,V2=V0/2
T0Vγ−10=T2(V02)γ−1⇒T2=T0√2
ΔU=(n1+n2)CV(T2−T0)
=43×0.2R(T0√2−T0)
ΔU=83RT0(√2−1)
Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Exercise 2.1
Explore 20 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Exercise 2.2
Explore 28 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
Similar Questions
A weightless piston divides a thermally insulated cylinder into two equal parts. One part contains one mole of an ideal gas with adiabatic exponent γ, the other is evacuated. The initial gas temperature is T0. The piston is released and the gas fills the whole volume of the cylinder. Then the piston is slowly displaced back to the initial position. Find the increment of the internal energy and entropy of the gas was resulting from these two processes.
View SolutionA weightless piston divides a thermally insulated cylinder into two parts of volumes V and 3V.2 moles of an ideal gas at pressure P=2 atmosphere are confined to the part with volume V=1 litre. The remainder of the cylinder is evacuated. The piston is now released and the gas expands to fill the entire space of the cylinder. The piston is then pressed back to the initial position. Find the increase of internal energy in the process and final temperature of the gas. The ratio of the specific heats of the gas, γ=1.5.
View Solution
Knowledge Check
A thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are P and T for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
AdecreaseBincreaseCremain sameDnone of these.A thermally insulated container is divided into two parts by a screen. In one part the pressure and temperature are P and T for an ideal gas filled. In the second part it is vacuum. If now a small hole is created in the screen, then the temperature of the gas will
AdecreaseBincreaseCremain sameDnone of theseTwo moles of an ideal gas is contained in a cylinder fitted with a frictionless movalbe piston, exposed to the atmosphere, at an initial temperature T0. The gas is slowly heated so that its volume becomes fout times the initial value. The wor done by gas is
AzeroB2RT0C4RT0D6RT0
A mass less piston divides a thermally insulated cylinder into two parts having volumes V = 2.5 litre and 3 V = 7.5 litre. 0.1 mole of an ideal gas is confined into the part with volume V at a pressure of P=105N/m2. The other part of the cylinder is empty. The piston is now released and the gas expands to occupy the entire volume of the cylinder. Now the piston is pressed back to its initial position. Find final temperature of the gas.
[Take R=253Jmol−1K−1 and γ=1.5 for the gas]
View SolutionA piston divides a closed gas cylinder into two parts. Initially the piston is kept pressed such that one part has a pressure P and volume 5V and the other part has pressure 8P and volume V, the piston is now left free. Find the new pressure and volume for the isothermal and aidabatic process. (γ=1.5)
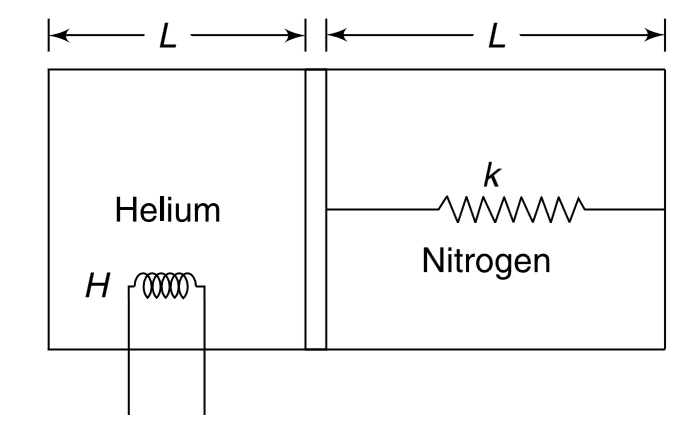
View SolutionAn adiabatic cylinder has length 2 L and cross sectional area A. A freely moving non conducting piston of negligible thickness divides the cylinder into two equal parts. The piston is connected to the right face of the cylinder with an ideal spring of force constant k. The right chamber contains 28 g nitrogen in which one third of the molecules are dissociated into atoms. The left chamber container 4 g helium. With piston in equilibrium and spring relaxed the pressure in both chamber is P0. The helium chamber is slowly given heat using an electric heater (H), till the piston moves to right by a distance 3L4. Neglect the volume occupied by the spring and the heating coil. Also neglect heat capacity of the spring.
(a) Find the ratio of CP and CV for nitrogen gas in right chamber.
(b) Calculate change in temperature of helium.
(c) Calculate heat supplied by the heater.
View Solution(i) A conducting piston divides a closed thermally insulated cylinder into two equal parts. The piston can slide inside the cylinder without friction. The two parts of the cylinder contain equal number of moles of an ideal gas at temperature T0. An external agent slowly moves the piston so as to increase the volume of one part and decrease that of the other. Write the gas temperature as a function of ratio (β) of the volumes of the larger and the smaller parts. The adiabatic exponent of the gas is γ.
(ii) In a closed container of volume V there is a mixture of oxygen and helium gases. The total mass of gas in the container is m gram. When Q amount of heat is added to the gas mixture its temperature rises by ΔT. Calculate change in pressure of the gas.
View SolutionA heat conducting piston can move freely inside a closed, thermally insulated cylinder with an ideal gas (γ= 5/3). At equilibrium, the piston divides the cylinder into two equal parts, the gas temperature being equal to 300 K. The piston is slowly displaced by an external agent. Find the gas temperature when the volume of the greater section is seven times the volume of the smaller section.
View Solution

