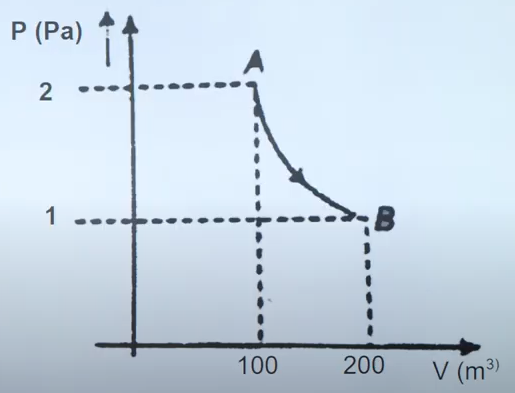
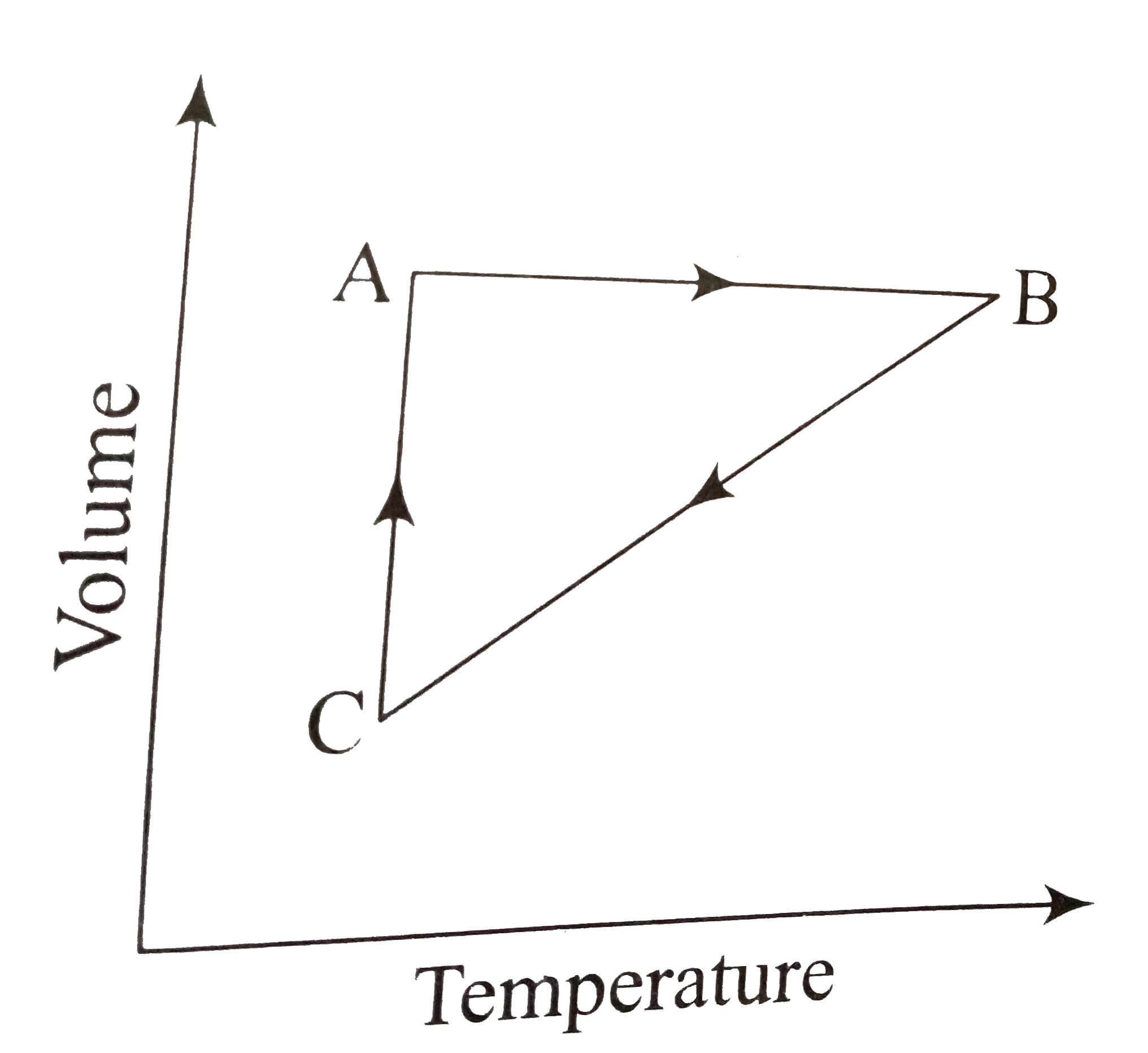
An ideal gas (2.0 moles) is carried round a cycle as shown. If the process b→c is isothermal and CV=3cal/mol/K. Determine
a. work done,
b. change in internal energy,
c. heat supplied to the system during processes a→b, b→c and c→a.
a. Work done , W
process a→b is clearly isobaric at P = 4 atm.
W=P(Vb−Va)=4(16.4−82)=32.8Latm
⇒Wa−b=32.8−101=3313J
Process b→c is isothermal (given)
W=2.303nRTlog(Vc/Vb)
⇒W=2.303(PbVb)log(Vc/Vb)
W=2.303(4×16.4×101)log(8.2/16.4)
Wb→c=−4592.5J
Process c→a is isochoric (volume is constant)
Wc→a=0J
b. change in internal energy ΔU
Process c→a:ΔU=nCvΔT
ΔU=nCv(PbVbnR−PaVanR) (since pV = nRT)
=CvR(P0V0−PaVa)=30.0821(4×16.4−4×8.2)
⇒ΔU=1200 cal
Process b→c : isothermal, ΔT=0
⇒ΔU=0
Process c→ΔU for complete cyclic process is zero because it depends on initial and final states i.e., temperature difference only.
(ΔU)ab+(ΔU)bc+(ΔU)ca=0
⇒1200+0+(ΔU)ca=0
⇒(ΔU)ca=−1200 col
Heat supplied : ΔH
Using the first law of thermodynamics:
(ΔH)ab=(ΔU)ab+Wab
=(1200+3313/4.18)cal=1992.5cal
⇒(ΔQ)ab=1992.5cal
⇒(ΔH)bc=(ΔU)bc+Wbc
=(0−4592.5/4.18)cal=1098.7cal
⇒(ΔH)bc=1098.7cal
(ΔH)ca=(ΔU)ca+Wca=−1200+0=−1200cal
⇒ΔH=1200cal

Topper's Solved these Questions
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Exercise 2.1
Explore 20 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Exercise 2.2
Explore 28 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSExercise:Interger
Explore 11 Videos
- KINETIC THEORY OF GASESBook:CENGAGE PHYSICSChapter:KINETIC THEORY OF GASESExercise:Compression
Explore 2 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBook:CENGAGE PHYSICSChapter:LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONExercise:Multiple Correct Answer Type
Explore 9 Videos
Similar Questions
Knowledge Check
Graph for one mole gas is given below

Work done in the process C→A isAZeroB8.21 L atmC16.2 L atmDUnpredictableIf work done by the system is 300 joule when 100 cal. Heat is supplied to it. The change in internal energy during the process is :-
A−200 JoulB400 JoulC720 JoulD120 JoulAn ideal gas is taken through the cycle A→B→C→A, as shown in figure. If the net heat supplied to the gas in the cycle is 5J, the work done by the gas in the process C→A is
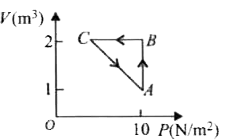 A−5JB−10JC−15JD−20J
A−5JB−10JC−15JD−20J
An ideal gas undergoes a series of processes represented bya→B→C→D on the P-V diagram. Answer the following questions.
(a) Is the internal energy of the gas at B and D equal?
(b) Find work done by the gas in the process A rarr B rarr C rarr D.
(c) Is it right to say that point B and D lie on an isotherm?
(d) Find the ratio of internal energy of the gas in state A to that in state D.
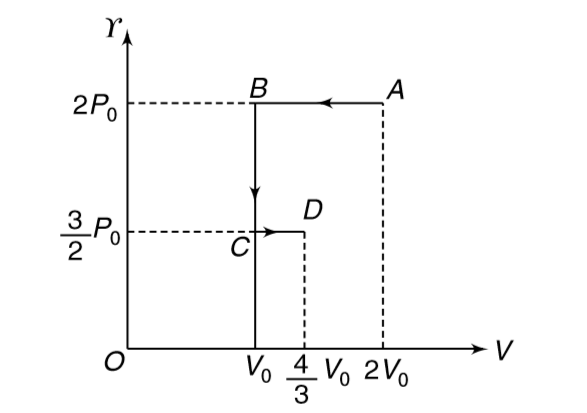
View SolutionAn ideal gas is taken through a thermodynamic cycle ABCDA. In state A pressure and volume are P0 and V0 respectively. During the process A→B, work done by the gas is zero and its temperature increases two fold. During the process B→C, internal energy of the gas remains constant but work done by it is WBC=–P0V0ln2. In the process C→D, the temperature decreases by 50% while the volume does not change. In the process D→A the temperature of the gas does not change.
(a) Draw pressure – volume (P–V) and pressure – density (P–ρ) graph for the cyclic process.
(b) Calculate work done on the gas during the cycle.
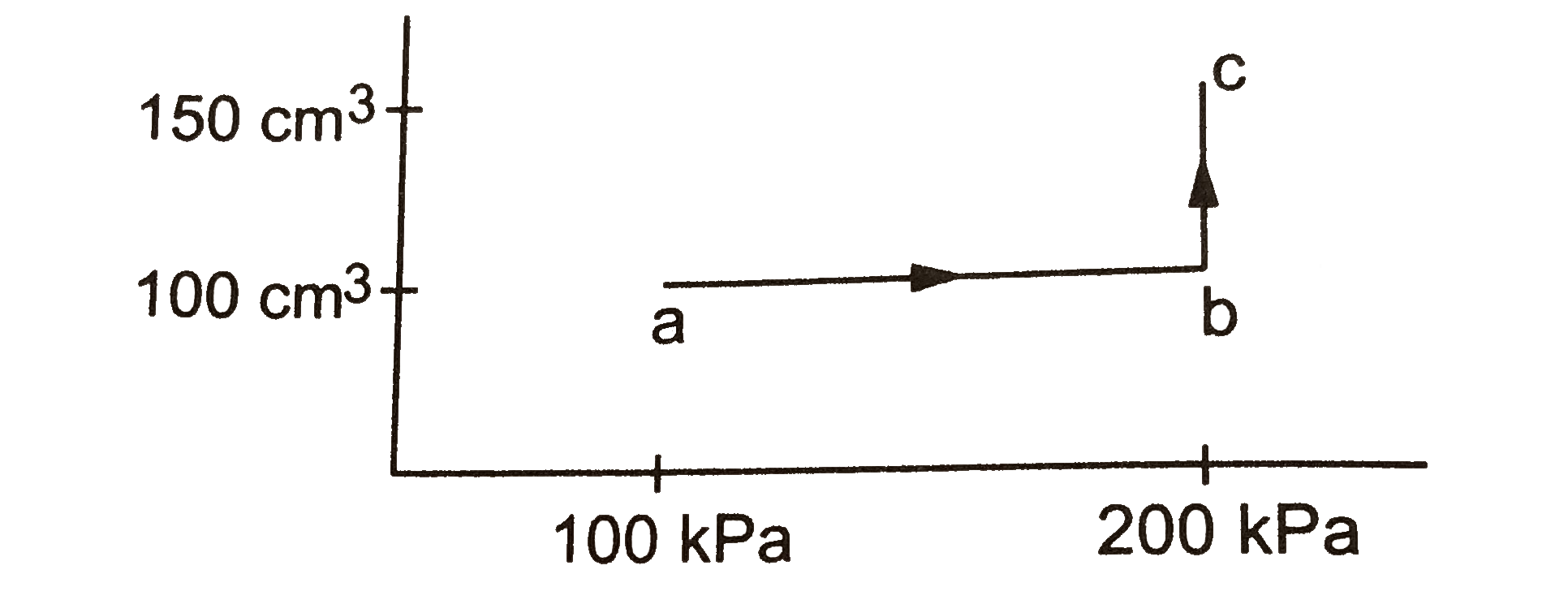
View SolutionAn ideal gas (γ=1.67) is taken through the process abc shown in figure . The temperature at the point a is 300k. Calculate (a) the temperature at b and c, (b) the work done in the process, ( c) the amount of heat supplied in the path ab and in the path bc and (d) the change in the internal energy of the gas in the process.
View SolutionOne mole of a monatomic gas is taken from a point A to another point B along the path ACB. The initial temperature at A is T0. Calculate the heat abosrbed by the gas in the process A→C→B.

View SolutionFive mole of a gas put through a series of change as shown below graphically in a cyclic process. The processes A→B,B→C and C→A, respectively, are
View Solution