A man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
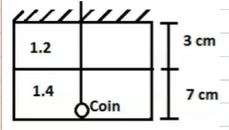
The correct Answer is:8
[8]
d=3.61.2+71.4=8
Related Playlists
- BOOK - FIITJEECHAPTER - TEST PAPERSEXERCISE - PHYSICS747videos
TEST PAPERS
- BOOK - FIITJEECHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Assignment Problems (Objective) (Level-II)20videos
SIMPLE HARMONIC MOTION
- BOOK - FIITJEECHAPTER - WORK, ENERGY AND POWER EXERCISE - COMPREHENSIONS ( Comprehension-II)5videos
WORK, ENERGY AND POWER
Knowledge Check
- Question 1 - Select One
A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
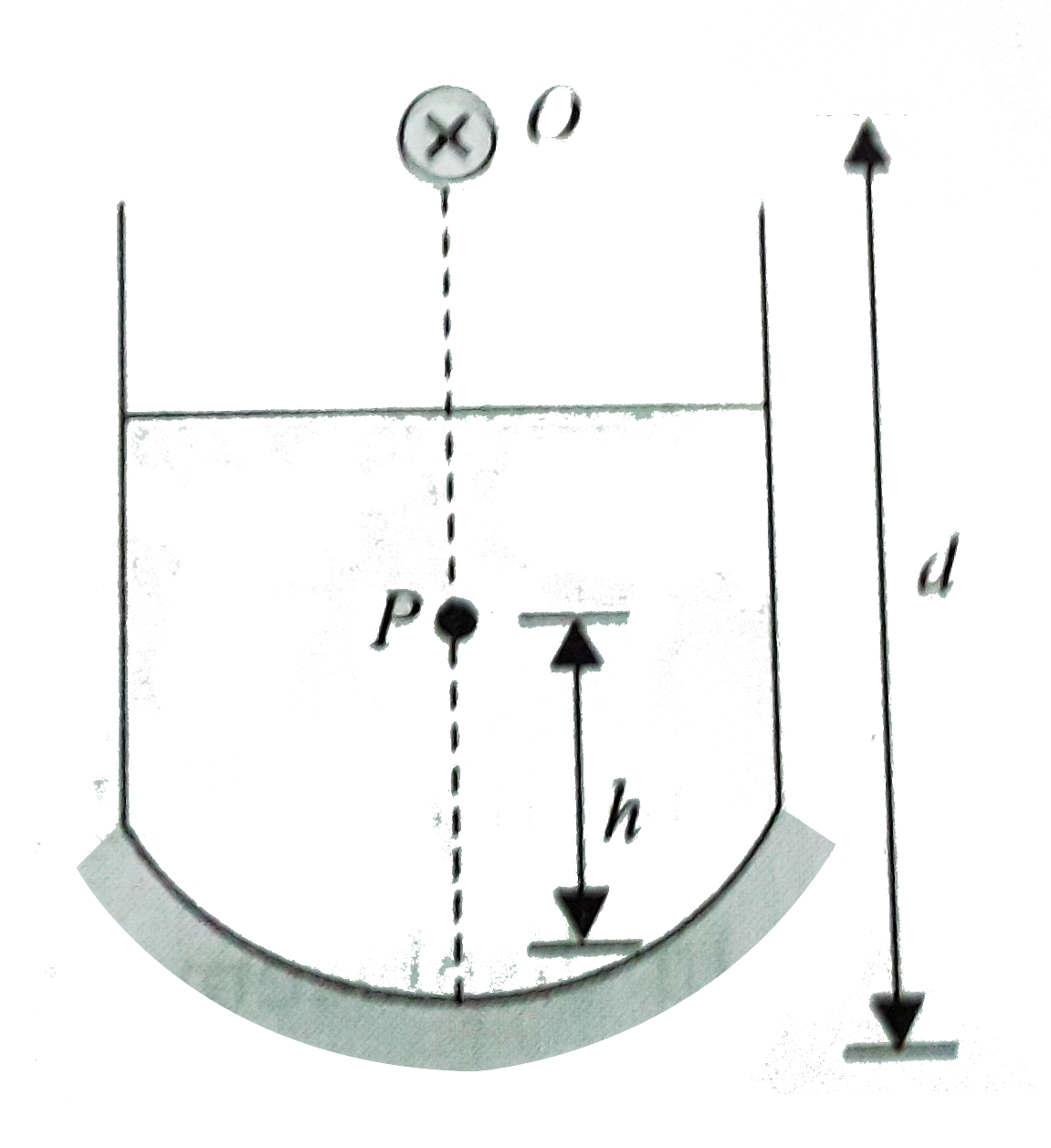 Ah(1−1μ)B2hμ−1CzeroD2hμ
Ah(1−1μ)B2hμ−1CzeroD2hμ - Question 1 - Select One

A real image of an object is formed by a conex lens at the bottom of an empty beaker. The beaker is now filled with a liquid of refractive index 1.4 to a depth of 7 cm. In order to get the image again at the bottom the beaker shoud be movedAdownward by 2 cmBupward by 2 cmCdownward by 3 cmDupward by 3 cm - Question 1 - Select One

Two liquids which do not react chemically are placed in a bent tube as shown in figure. The height of the liquids above their surface of separation areAdirectly proportional to their densitiesBinversely proportional to their densitiesCdirectly proportional to square of their densitiesDinversely proportional to square of theire densities. - Question 1 - Select One
A beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
A(d1×d2d1+d2)((1μ1)+(1μ2))B(μ1×μ2)(d1+d2)C((d1μ2)+(d2μ1))D⎛⎜⎝d1μ1d2μ2⎞⎟⎠
Similar Questions
A coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
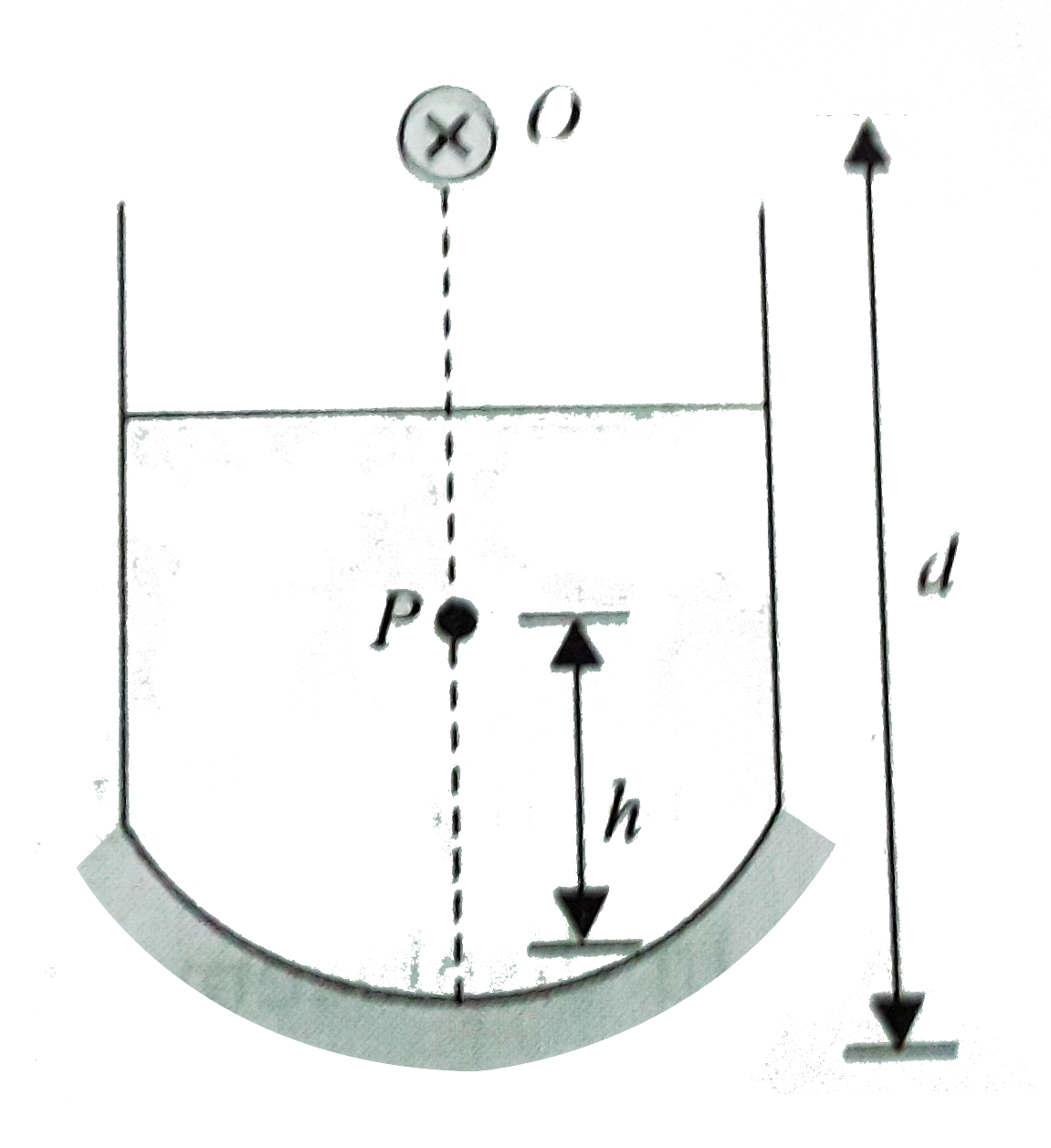 View Solution
View SolutionA coin is placed at the bottom of a beaker containing water (refractive index=4/3) at a depth of 12cm. By what height the coin appears to be raised when seen from vertical above ?
View Solution
Two liquids which do not react chemically are placed in a bent tube as shown in figure. The height of the liquids above their surface of separation areView SolutionA beaker is filled with two immiscible transparent liquids of refractive indices μ1 and μ2 having thickness of layers d1 and d2 respectively. The apparent depth of the bottom of the beaker is
View SolutionAn object is located at the bottom of a tank containing two immiscible liquids and is seen vertically from above. The lower and upper liquids are of depths h1 and h2 respectively and of refractive indices μ1 and μ2 respectively. Locate the position of the image of the object O from the surface.
View Solution

