An object is located at the bottom of a tank containing two immiscible liquids and is seen vertically from above. The lower and upper liquids are of depths h1 and h2 respectively and of refractive indices μ1 and μ2 respectively. Locate the position of the image of the object O from the surface.

Shift by (1): h1(1−1/μ1)
Shift by (2): h2(1−1/μ2)
Total shift OI=h1(1−1/μ1)+h2(1−1/μ2)
Distance of final image from P
PI=PO−OI
=(h1+h2)−[h1(1−1/μ1)+h2(1−1/μ2)]
=h1μ1+h2μ2
Topper's Solved these Questions
- REFRACTION OF LIGHT BY PLANE SURFACESBOOK - CP SINGHCHAPTER - REFRACTION OF LIGHT BY PLANE SURFACESEXERCISE - Exercises
110 Videos
- REFRACTION AT SPHERICAL SURFACESBOOK - CP SINGHCHAPTER - REFRACTION AT SPHERICAL SURFACESEXERCISE - EXERCISES
105 Videos
- SEMICONDUCTORSBOOK - CP SINGHCHAPTER - SEMICONDUCTORSEXERCISE - Exercises
140 Videos
Similar Questions
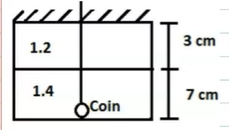
A man observes a coin placed at the bottom of a beaker which contains two immiscible liquids of refractive indices 1.2 and 1.4 as shown in the figure. Find the depth of the coin below the surface, as observed from above.
View SolutionAn object is placed at the bottom of a tank filled with liquid of refractive index 1.6. If the actual depth of the tank is 10 cm, what will be the apparent depth of the object?
View Solution
Knowledge Check
A tank contains two different liquids which do not mix with each other. The lower and upper liquid are at depth h1 and h2 respectively and of refractive indices μ1 and μ2. An object O is located at the bottom, when see vertically from above. Locate the position of image of the object O as seen from above.
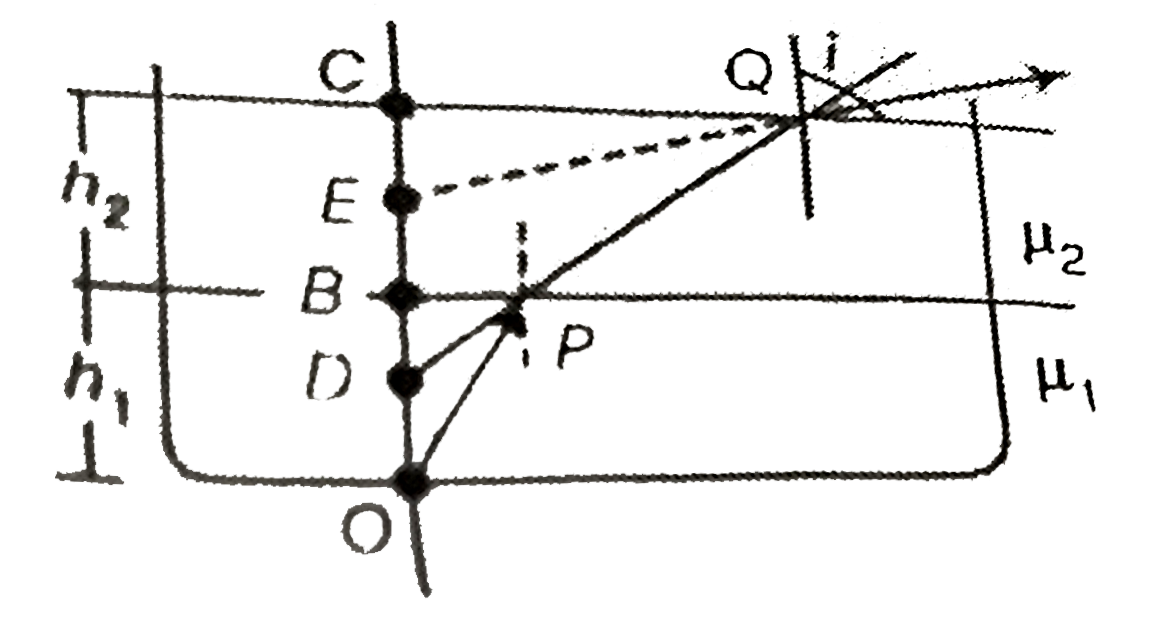 Ah1μ1−h2μ2Bh1μ1+h2μ2Ch1μ1+h2μ1Dh1μ2−h2μ1
Ah1μ1−h2μ2Bh1μ1+h2μ2Ch1μ1+h2μ1Dh1μ2−h2μ1The length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
Aμ1d1+μ2d2Bμ1d2+μ2d1Cd1d3μ1μ2Dd1+d2μ3μ2The length of the optical path of two media in contact of length d1 and d2 of refractive indices μ1 and μ2 respectively, is
Aμ1d1+μ2d2Bμ1d2+μ2d1Cd1d2μ1μ2Dd1+d2μ1μ2
A jar contains two immiscible liquids A and B with a coin at its bottom. The depths of liquid A and liquid B are 6 cm and 8 cm, respectively. If the apparent depth of the coin is 9 cm and refractive index of liquid A is 1.5, what is the refractive index of liquid B?
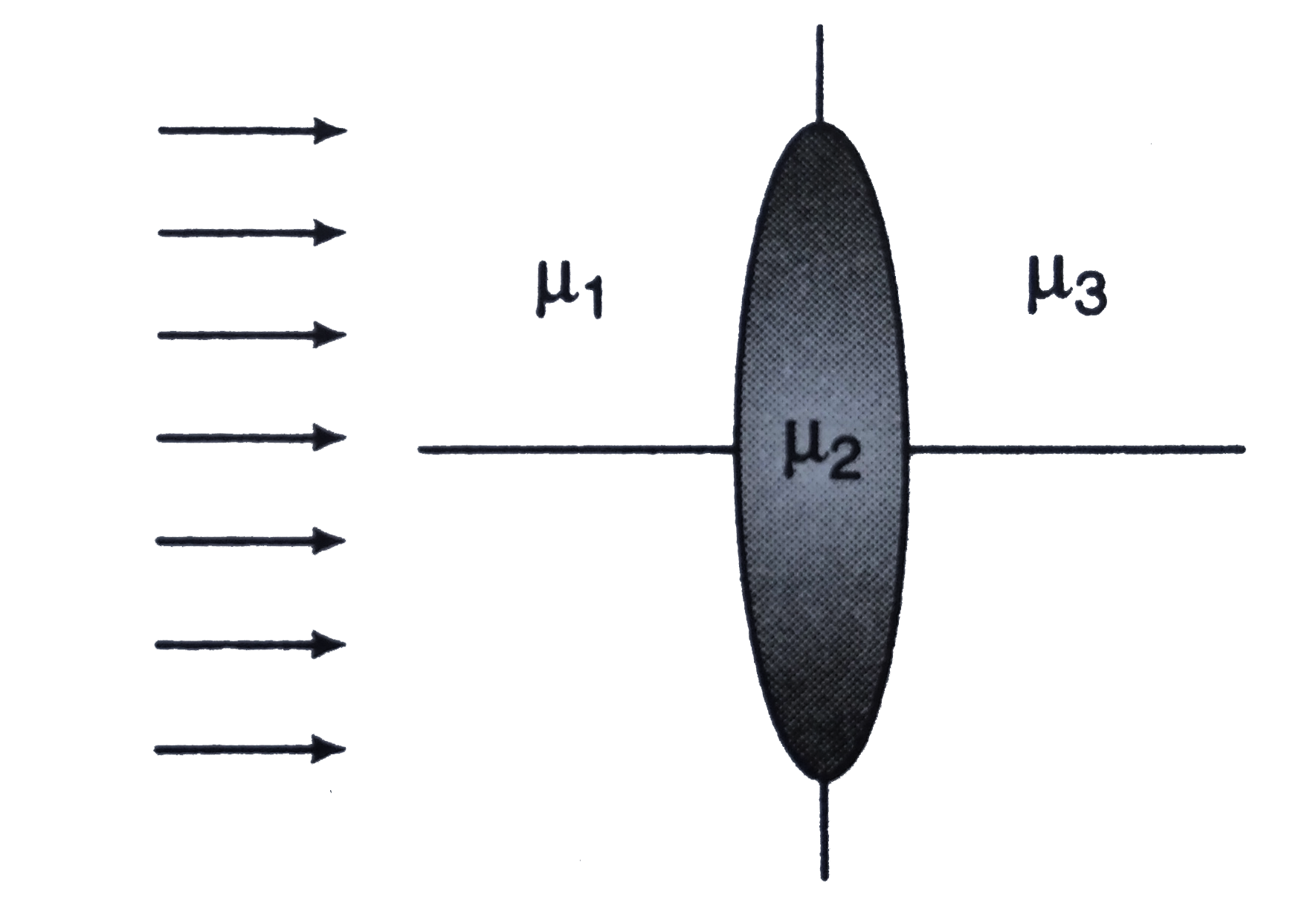
View SolutionA thin glass lens of refractive index μ2=1.5 behaves as an interface between two media of refractive indices μ1=1.4andμ3=1.6 respectively. Determine the focal length of the lens for the shown arrangement of radius of curvature of both surfaces 20cm.
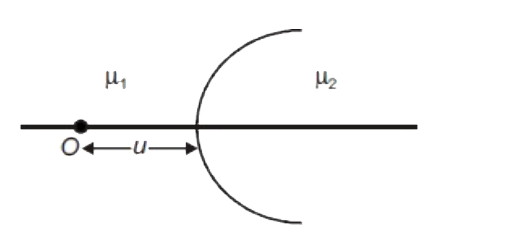
View SolutionThe diagram shows a spherical surface which separates two media of refractive index, μ1andμ2. Respectively. Now, a point object is placed on the principal axis as shown in the figure. Then
View SolutionIf μ1andμ2 are the refractive indices of the material of core and cladding respectively of an optical fiber, then
View SolutionFor statement of question 118, if the heights of the two images are h1 and h2 , respectively,then the height of the object (h) is
View Solution
