A circular ring of radius a is made from a wire having resistance (λ) per unit length. The ring is mounted on a car such that ring remains vertical. The care moves along a horizontal circle of radius R and completes n revolutions per minute. The horizontal component of earth's magnetic field be H,
Calculate average rate at which heat is produced in the ring
π3a3H2n21800λJs−1
π3a3H2n23600λJs−1
π3a3H2n21200λJs−1
None of these
The correct Answer is:B
Path of the car is a circle of radius R as shown in fig. Let at instant t=0, the car be at A when
the axis of ring was parallel to horizontal component H of earth's magnetism. Since, car completes n revolutions per mintues, therefore, angular velocity of car is ω=(2πn60)
Hence, at time t, its position B is given by,
θ=ωt=2πnt60=πnt30
Axis of the ring has also turned through the same angle θ. Therefore, component of H along ring axis is now equal to H cos θ.
Hence, Flux linked with the ring at this instant is ,
ϕ=πa2(Hcosθ)=πa2Hcos(πnt30)
Induced emf,
e=−dϕdt=π2a2nH30sin(πnt30)
Resistance of the ring = 2πal.
Due to induced emf, a current starts to flowing through the ring and due to this current heat is produced in the ring. At time t, thermal power.
P=(e2Resistance)
Perio of one complete revolution of the car is ,
Pavg=∫t0pdtT=π3a2H2n23600λjs−1.

Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Integer12videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 5EXERCISE - Multiple Correct34videos
MISCELLANEOUS VOLUME 5
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS VOLUME 3EXERCISE - True and False3videos
MISCELLANEOUS VOLUME 3
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - NUCLEAR PHYSICSEXERCISE - ddp.5.514videos
NUCLEAR PHYSICS
Similar Questions
A circular ring of radius a is made from a wire having resistance (λ) per unit length. The ring is mounted on a car such that ring remains vertical. The care moves along a horizontal circle of radius R and completes n revolutions per minute. The horizontal component of earth's magnetic field be H,
The emf induced in the ring isView SolutionA horizontal ring of radius r=12m is kept in a vertical constant magentic field 1T. The ring is collapsed from maximum area to zero area in 1s. Then the emf induced in the ring is
View Solution
Knowledge Check
- Question 1 - Select One
A wheel with 20 metallic spokes each of length 8.0 m long is rotated with a speed of 120 revolution per minute in a plane normal to the horizontal component of earth magnetic field H at a place. If H=0.4×10−4 T at the place, then induced emf between the axle the rim of the wheel is
A2.3×10−4VB3.1×10−4VC2.9×10−4VD1.61×10−4V

A small part of dl length is removed from a ring having charge per unit length λ. Find electric field at centre due to remaining ring.View SolutionFind the equivalent resistance between A and B.
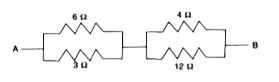 View Solution
View SolutionA circular coil of mean radius of 7cm and having 4000 turns Is rotate at the rate of 1800 revolution per minute in the earth 's magnetic field (B=0.5 gauss), the maximum e.m.f. induced in coil will be
View SolutionA vertical conducting ring of radius R falls vertically with a speed V in a horizontal uniform magnetic field B which is perpendicular to the plane of the ring. Which of the following statements is correct?
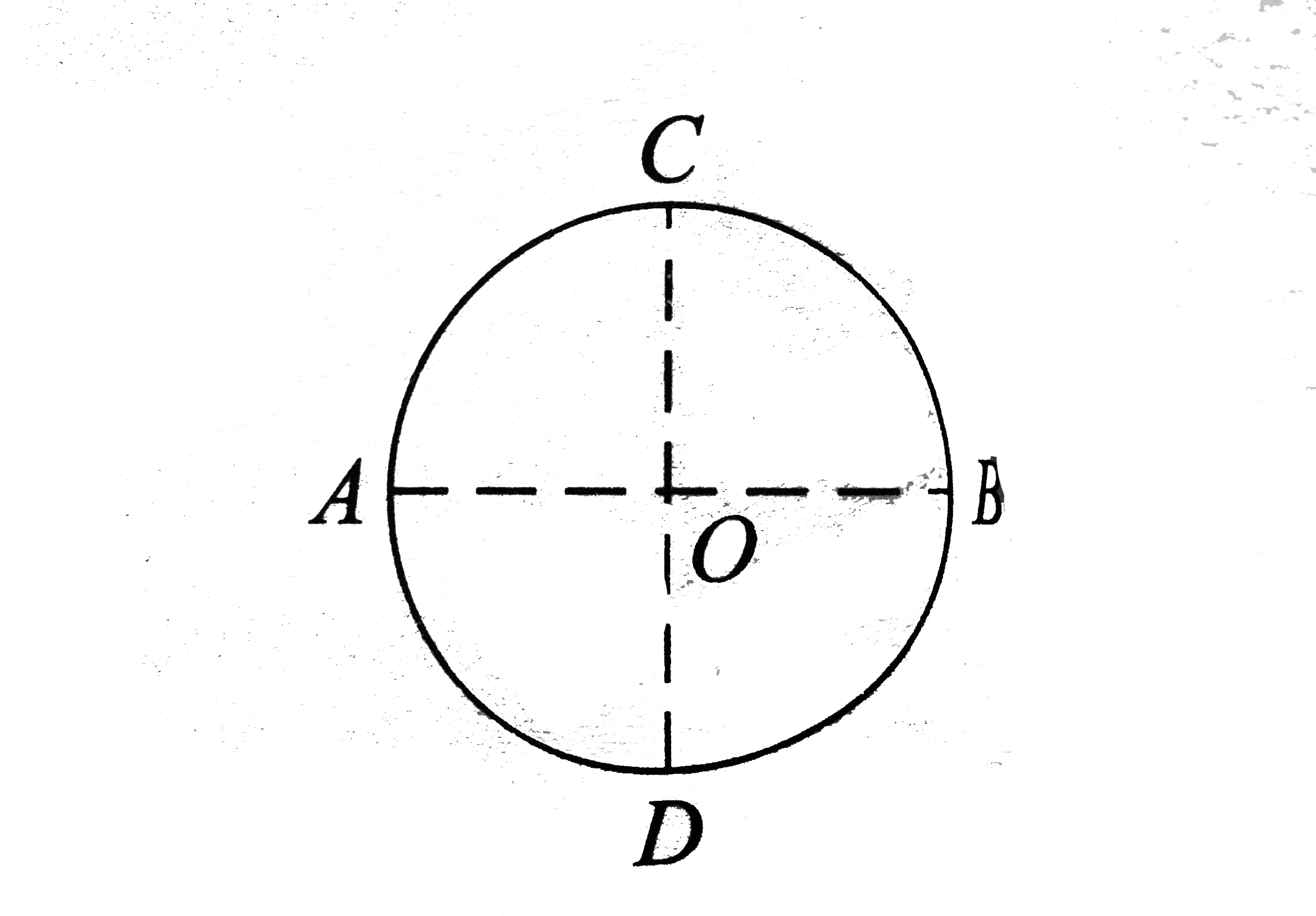 View Solution
View SolutionSTATEMENT-1
A vertical iron rod has a coil of wire wound over it at the bottom end.An alternating current flows in the coil.The rod goes through a conducting ring as shown in the figure.The ring can float at a certain height above the coil.
because
STATEMENT-2
In the above situation, a current is induced in the ring which interacts with the horizontal component of the magnetic field to produce an average force in the upward direction
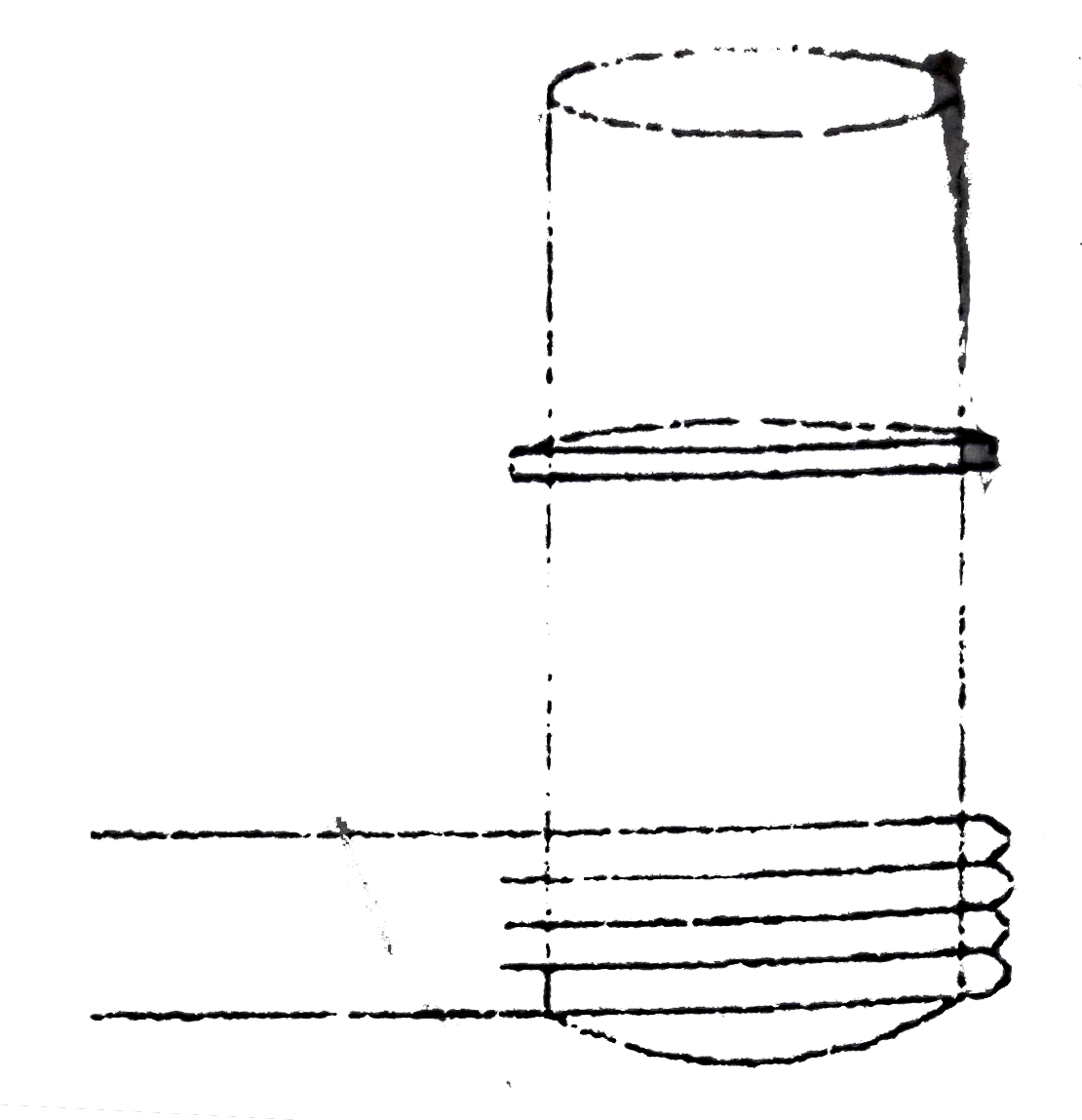 View Solution
View SolutionTwo long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.
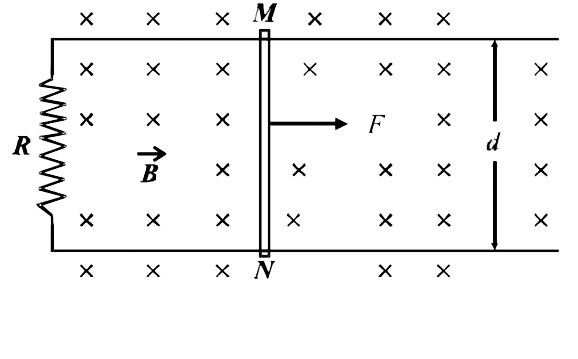
(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View Solution
