Two long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.
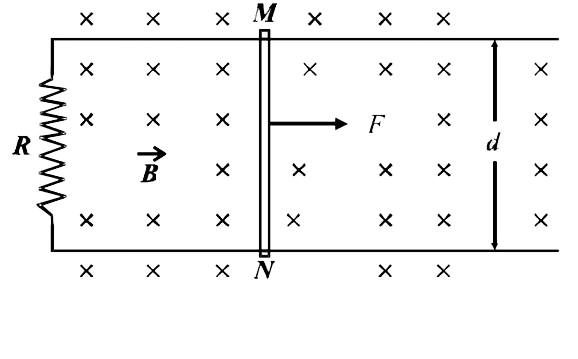
(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?
(a) If the rod has instantaneous velocity v at a distance x from R, the include emf is Bvd.
∴ Induced I=BvdR+2λx=constant
∴ Velocity v=(R+2λx)iBd
Megnetic force on the rod =B.
This force will be opposite to F. Hence, net force acting in rod,
F−Bmdvdt
or F−Bid=mdvdxdxdt=mvddx{(R+2λx)ibd}=mv2λiBd
∴ F=Bid+2mλ(R+2λx)B2d2i2
(b) Work done per second per second =Fv
Heat produced per second =i2(R+2λx)
Requiredratio=i2(R+2λx)BdF(R+2λx)i=iBdF
=BidBid+2mλ(R+2λx)i2B2d2
=11+2mλ(R+2λx)i2B3d3
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Solved Example
5 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercise 3.1
15 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A square loop of side 'a' with a capacitor of capacitance C is located between two current carrying long parallel wires as shown. The value of I in the wires in given as I=(I0)sinωt.
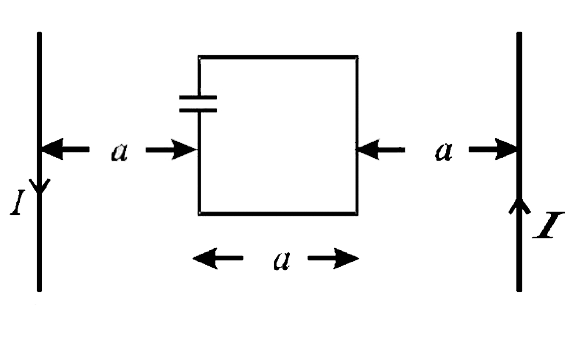
(a) Calculate maximum current in the square loop.
(b) Draw a graph between charges on the upper plates of the capacitor vs time.
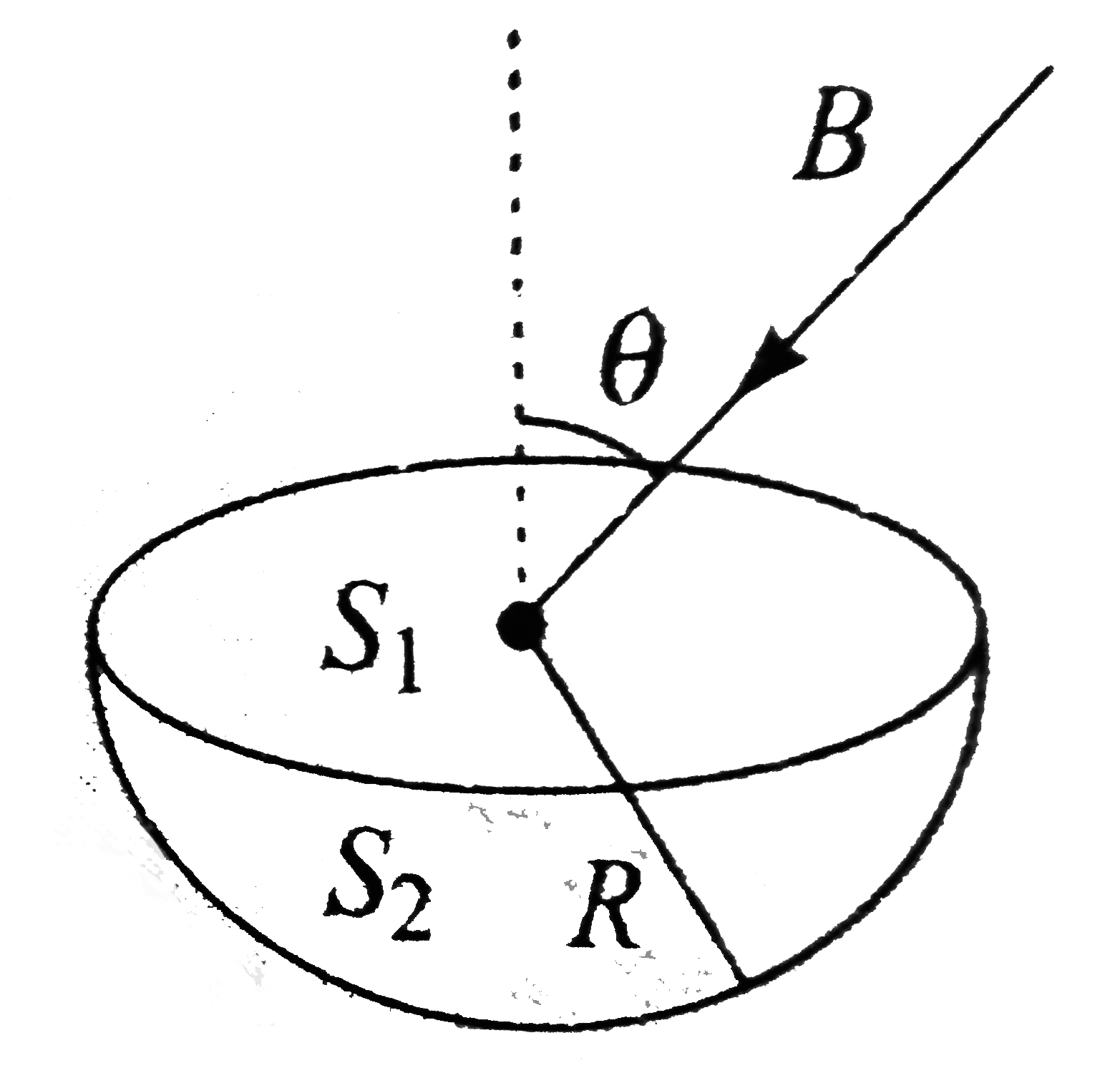
View SolutionConsider the hemispherical closed surface as shown in Fig. 3.19. if the hemisphere is a uniform magnetic field that makes an angle θ with the vertical, calculate the magnetic flux
(a) through the flat surface S1.
(b) through the hemisphere surface S2.
View SolutionThe measurement of an unknown resistance R is to be carried out using Wheatstone bridge (see Fig. 2(EP).3). Two students perform an experiment in two way. The first student takes R2=10Ω and R1=5Ω. The other student takes R2=1000Ω and R1=500Ω. In the standard arm, both take R3=5Ω. Both find R=R2R1R3=10Ω within errors.
View SolutionThe figure shows different graphs between stopping potential (V0) and frequency (v) for photosensitive surface of cesium , potassium , sodium and lithium. The plots are parallel. Correct ranking of the targets according to their work function greatest forst will be

View SolutionTwo long parallel horizontal rails a, a distance d aprt and each having a risistance λ per unit length are joing at one end by a resistance R. A perfectly conduction rod MN of mass m is free to slide along the rails without friction (see figure). There is a uniform magnetic field of induction B normal to the plane of the paper and directed into the paper. A variable force F is applied to the rod MN such that, as the rod moves a constant current flows through R.

(i) Find the velocity of the rod and the applied force F as function of the distance x of the rod from R.
(ii) What fraction of the work done per second by F is converted into heat?
View SolutionShows a rod of length l and resistance r moving on two rails shorted by a resistance R . A uniform magnetic field B is present normal to the plane of rod and rails. Show the electrical equivalence of each branch.
View SolutionA wire of length l , mass m and resistance R slides without any friction down the parallel conducting rails of negligible resistance . The rails are connected to each other at the bottom by a resistanceless rail parallel to the wire so that the wire and the rails form a closed rectangualr conducting loop. The plane of the rails makes an angle theta with the horizontal and a uniform vertical magnetic field of the inducetion B exists throughout the rregion. Find the steady state velocity of the wire.
View SolutionA pair of parallel conducting rails lie at right angle to a uniform magnetic field of 2.0T as shown in the fig. two resistor 10Omega and 5Omega are to slide without friction along the rail. The distance between the conducting rails is 0.1m . Then
View SolutionA copper rod of mass m slides under gravity on two smooth parallel rails l distance apart set at an angle theta to the horizontal. At the bottom, the rails are joined by a resistance R . There is a uniform magnetic field perpendicular to the plane of the rails. the terminal valocity of the rod is
View SolutionIn the shown figure, there are two long fixed parallel conducting rails (having negligible resistance) and are separated by distance L . A uniform rod of resistance R and mass M is placed at rest on frictionless rails. Now at time t = 0 , a capacitor having charge Q_(0) and capacitance C is connected across rails at ends a and b such that current in rod (c d) is from c towards d and the rod is released. A uniform and constant magnetic field having magnitude B exists normal to plane of paper as shown. (Neglect acceleration due to gravity) When the acceleration of rod is zero, the speed of rod is :
View SolutionA conducting rod of mass m and length l is free to move without friction on two parallel long conducting rails, as shown below. There is a resistance R across the rails. In the entire space around, there is a uniform magnetic field B normal to the plane of the rod and rails. The rod is given an impulsive velocity v0-

Finally, the initial energy 12mv20
View SolutionA pair of long, smooth, parallel, horizontal, conducting rails are joined to a cell at one end. There are no external electric or magnetic fields. A metal rod is placed on the rails. The rod will
View SolutionTwo long parallel horizonal rails , a distance d apart and each having a resistance λ per unit length are jointed at one end by a resitance R. A perfectly conducting rod MN of mass m is free to slide along the rails . A variable force F is applied to the rod MN , such that ,as the rd moves, a constant current i flows through R.
(a) Find the velocity v and the force F as function of the function of the distance x of the rod from R.
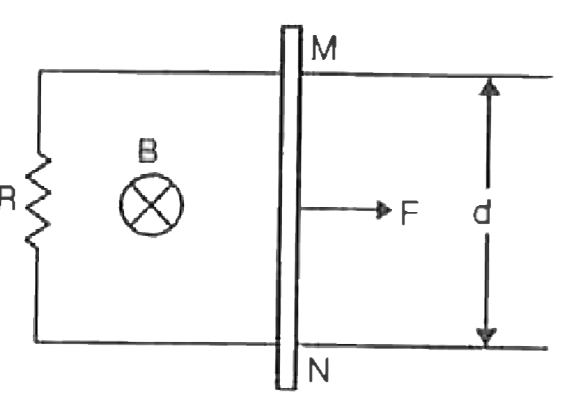
(b) What fraction η of the work done by F per second in converted into heat ?
View Solution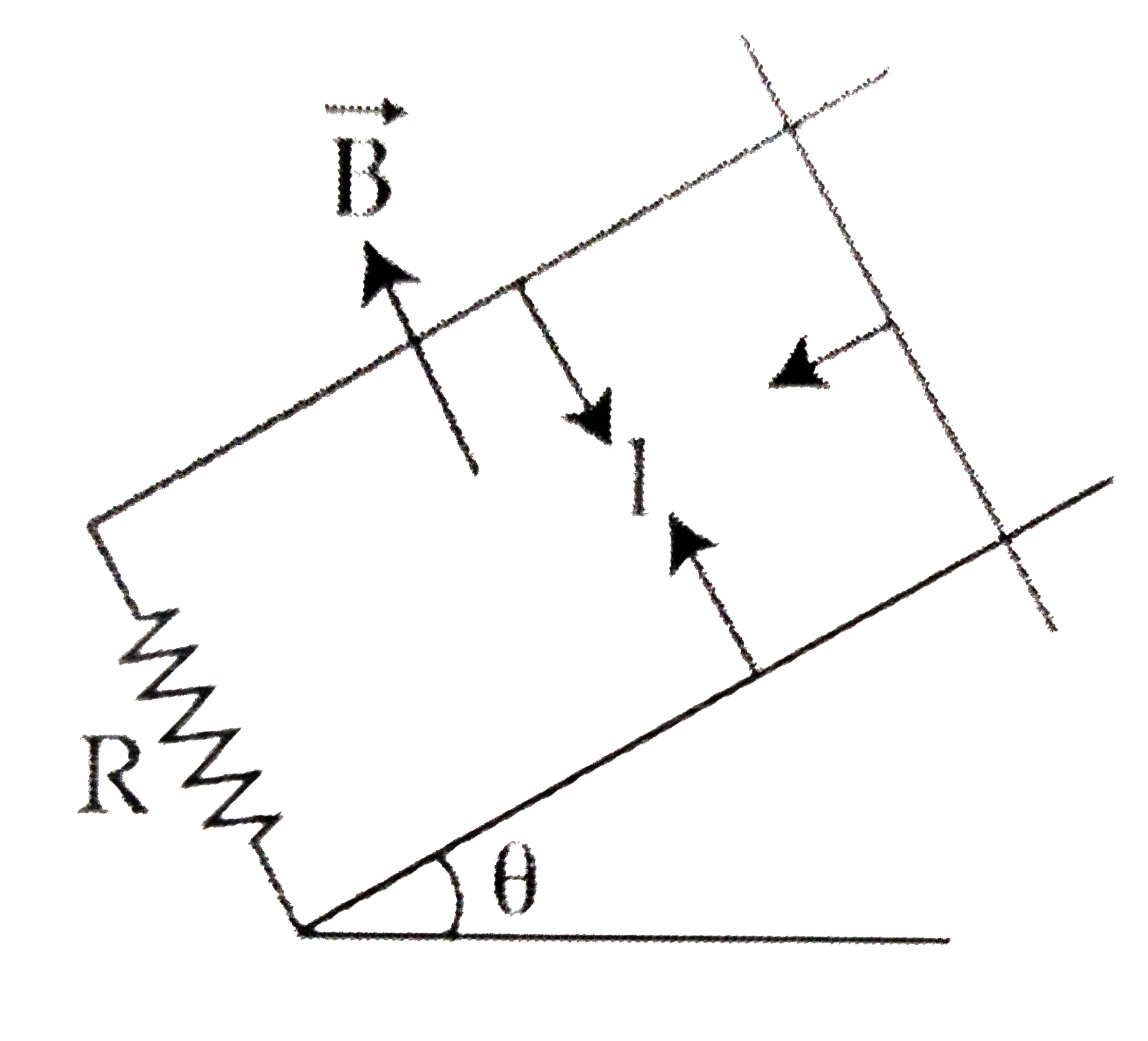
a copper rod of mass m slides under gravity on two smooth parallel rails with separation I and set at an angle of θ with the horiziontal at the bottom rails are joined by resistance R. There is a uniform magnetic field B normal to the plane of the rails as shown in the figure The terminal speed of the copper rod is :
View Solutionदो लम्बी समान्तर क्षैतिज पटरियाँ जो परस्पर दूरी पर हैं तथा जिनमें प्रत्येक की एकांक लम्बाई का प्रतिरोधλ है, एक सिरे पर एक प्रतिरोध R द्वारा जुड़ी हैं। द्रव्यमान m की एक पूर्णतया चालक छड़ MN पटरियों पर बिना घर्षण के फिसलने के लिए स्वतन्त्र है। यहाँ पर एकसमान चुम्बकीय क्षेत्र B कागज के तल के लम्बवत् नीचे की ओर दिष्ट है। छड़ MN पर एक परिवर्ती बल (Variable force) F इस प्रकार लगाया गया है कि जैसे ही छड़ चलती है, R में एक नियत धारा । प्रवाहित होती है।
Rसे छड़ की दूरी x के फलन के रूप में छड़ का वेग तथा लगाया गया बल F ज्ञात कीजिए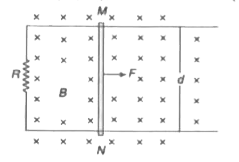
View Solution
