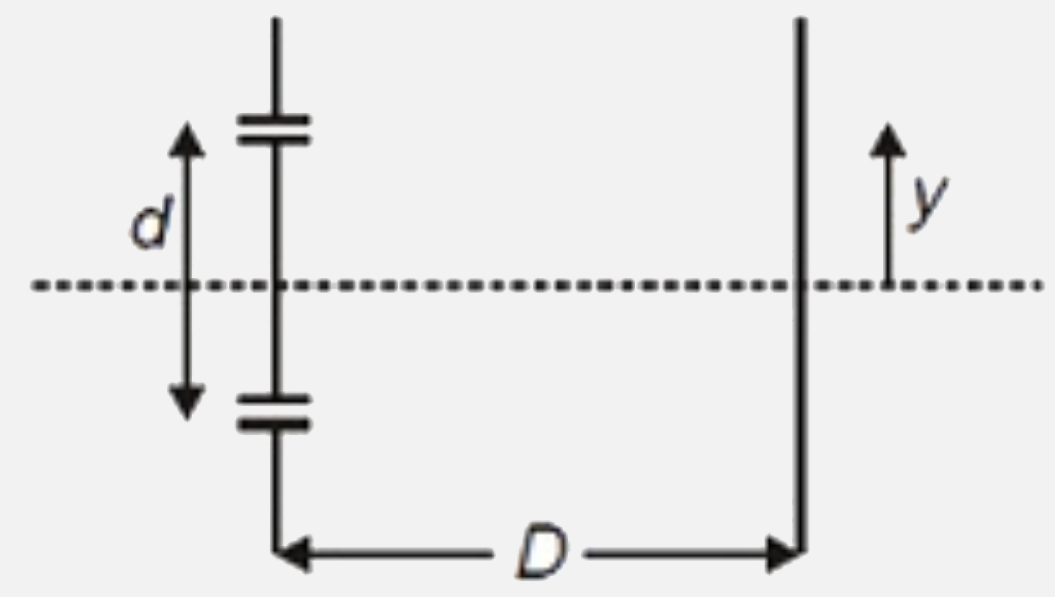
A beam of light consisting of wavelengths 6000 Å and 4500 Å is used in a YDSE with D = 1 m and d = 1 mm. Find the least distance from the central maxima, where bright fringes due to the two wavelengths coincide.
To solve the problem, we need to find the least distance from the central maxima where bright fringes due to two different wavelengths coincide in a Young's Double Slit Experiment (YDSE). Let's break down the steps:
Step 1: Understand the formula for fringe positions
In YDSE, the position of the bright fringes is given by:
yn=nλDd
where:
- yn = position of the nth bright fringe,
- n = order of the fringe (1, 2, 3,...),
- λ = wavelength of light,
- D = distance from the slits to the screen,
- d = distance between the slits.
Step 2: Write the expressions for the two wavelengths
For the two wavelengths given in the problem:
- Wavelength 1: λ1=6000Å=6000×10−10m
- Wavelength 2: λ2=4500Å=4500×10−10m
The positions of the bright fringes for each wavelength can be written as:
- For λ1:
y1=n1⋅6000×10−10⋅Dd
- For λ2:
y2=n2⋅4500×10−10⋅Dd
Step 3: Set the fringe positions equal to find coinciding maxima
To find the least distance where the bright fringes coincide, we set y1=y2:
n1⋅6000×10−10⋅Dd=n2⋅4500×10−10⋅Dd
Step 4: Simplify the equation
Cancel D and d from both sides:
n1⋅6000=n2⋅4500
Step 5: Rearrange to find the ratio of orders
Rearranging gives:
n1n2=45006000=34
Step 6: Choose values for n1 and n2
To find the least distance, we can choose:
- n1=3
- n2=4
This means the third maximum of the wavelength 6000Å coincides with the fourth maximum of the wavelength 4500Å.
Step 7: Calculate the distance from the central maxima
Using either n1 or n2:
y=y1=3⋅6000×10−10⋅Dd
Substituting D=1m and d=1mm=10−3m:
y=3⋅6000×10−10⋅110−3
y=3⋅6000×10−7
y=18×10−4m=1.8mm
Final Answer
The least distance from the central maxima where bright fringes due to the two wavelengths coincide is 1.8 mm.
---
In YDSE, the position of the bright fringes is given by:
yn=nλDd
where:
- yn = position of the nth bright fringe,
- n = order of the fringe (1, 2, 3,...),
- λ = wavelength of light,
- D = distance from the slits to the screen,
- d = distance between the slits.
For the two wavelengths given in the problem:
- Wavelength 1: λ1=6000Å=6000×10−10m
- Wavelength 2: λ2=4500Å=4500×10−10m
- For λ1:
y1=n1⋅6000×10−10⋅Dd
- For λ2:
y2=n2⋅4500×10−10⋅Dd
To find the least distance where the bright fringes coincide, we set y1=y2:
n1⋅6000×10−10⋅Dd=n2⋅4500×10−10⋅Dd
Cancel D and d from both sides:
n1⋅6000=n2⋅4500
Rearranging gives:
n1n2=45006000=34
To find the least distance, we can choose:
- n1=3
- n2=4
Using either n1 or n2:
y=y1=3⋅6000×10−10⋅Dd
y=3⋅6000×10−10⋅110−3
y=3⋅6000×10−7
y=18×10−4m=1.8mm
The least distance from the central maxima where bright fringes due to the two wavelengths coincide is 1.8 mm.
Topper's Solved these Questions
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Subjective
Explore 11 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Single Correct
Explore 128 Videos
- WAVE OPTICSBook:CENGAGE PHYSICS ENGLISHChapter:WAVE OPTICSExercise:Exercise 2.1
Explore 12 Videos
- SOURCES OF MAGNETIC FIELDBook:CENGAGE PHYSICS ENGLISHChapter:SOURCES OF MAGNETIC FIELDExercise:single correct Ansewer type
Explore 12 Videos
Similar Questions
In YDSE a parallel beam of incident light consists of two wavelengths λ1=4000Åandλ2=5600Å. The minimum distance y on the screen, measured from the central axis, where the bright fringe due to two wavelengths coincide is nλ1Dd. Find n.
View SolutionIn a Young's double slit experiment, slits are separated by 0.5mm and the screen is placed 150cm away. A beam of light consisting of two wavelengths, 650nm and 520nm, is used to obtain interference fringes on the screen. The least distance from the commom central maximum to the point where the bright fringes fue to both the wavelengths coincide is
View Solution
Knowledge Check
A beam of light consisting of two wavelengths 650nm and 520nm is used to obtain interference fringes in a Young's double slit experiment.
(a) Find the distance of the third bright fringe on the screen from the central maximum for the wavelength 650nm.
(b) What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide? The distance between the slits is 2mm and the distance between the plane of the slits and screen is 120cm.A1.17 mmB2.52 mmC1.56 mmD3.14 mm
A beam of light consisting of two wavelengths, 650 nm and 520 nm is used to obtain interference fringes in Young's double-slit experiment. What is the least distance (in m) from a central maximum where the bright fringes due to both the wavelengths coincide ? The distance between the slits is 3 mm and the distance between the plane of the slits and the screen is 150 cm.
View SolutionA beam of light consisting of two wavelengths 6500A0 and 5200A0 is used to obtain interference fringes in a Young.s double slit experiment.
What is the least distance from the central maximum where the bright fringes due to both the wavelengths coincide? Distance between the slits is 2mm, distance between the slits and the screen L=120cm.
View SolutionA beam of light consisting of two wavelenths, 6500 Å and 5200 Å is used to obtain interference fringes in a Young's double slit experiment (1Å=10−10m). The distance between the slits is 2.0 mm and the distance between the plane of the slits and the screen in 120 cm. (a) Find the distance of the third bright frings on the screen from the central maximum for the wavelength 6500 Å (b) What is the least distance from the central maximum where the bright frings due to both the wavlelengths coincide ?
View SolutionAnswer the following:
(a) In Young's double slit experiment, derive the condition for (i) constructive interference and (ii) destructive interference at a point on the screen.
(b) A beam of light consisting of two wavelengths, 800 nm and 600 nm is used to obtain the interference fringes in a Young's double slit experiment on a screen placed 1.4 m away. If the two slits are separated by 0.28 mm, calculate the least distance from the central bright maximum where the bright fringes of the two wavelengths coincide.
View SolutionA beam of light consisting of two wavelengths, 650 nm and 520 nm is used to obtain interference fringes in Young's double-slit experiment. What is the least distance (in m) from a central maximum where the bright fringes due to both the wavelengths coincide ? The distance between the slits is 3 mm and the distance between the plane of the slits and the screen is 150 cm.
View SolutionA beam of light consisting of two wavelength, 650 nm and 520 nm, is used to obtain interference fringes in a Young's double - slit experiment. Find the distance of the third bright fringe on the screen from the central maximum for wavelengths 650 nm.
View SolutionA beam of light consisting of two wavelengths 6500Å and 5200Å is used to obtain interference fringes in YDSE. The distance between slits is 2mm and the distance of the screen form slits is 120 cm. What is the least distance from central maximum where the bright due to both wavelengths coincide?
View Solution

