Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length 2√7 on y-axis is (are)
x2+y2+6x+8y+9=0
x2+y2+6x+7y+9=0
x2+y2+6x−8y+9=0
x2+y2+6x−7y+9=0
The correct Answer is:C
Here, length of intercept on Y-axis =2√f2−c and if circle touches X-axis ⇒g2=c,forx2+y2+2gx+2fy+c=0 passes through (3,0).<br> and 2√f2−c=2√7⇒f2−c=7 from egs. (i) and (ii). g2+6g+9=0⇒(g+3)2=0
∴g=−3andc=9
∴f2=7+c=16
⇒f=±4
∴x2+y2−6x±8y+9=0
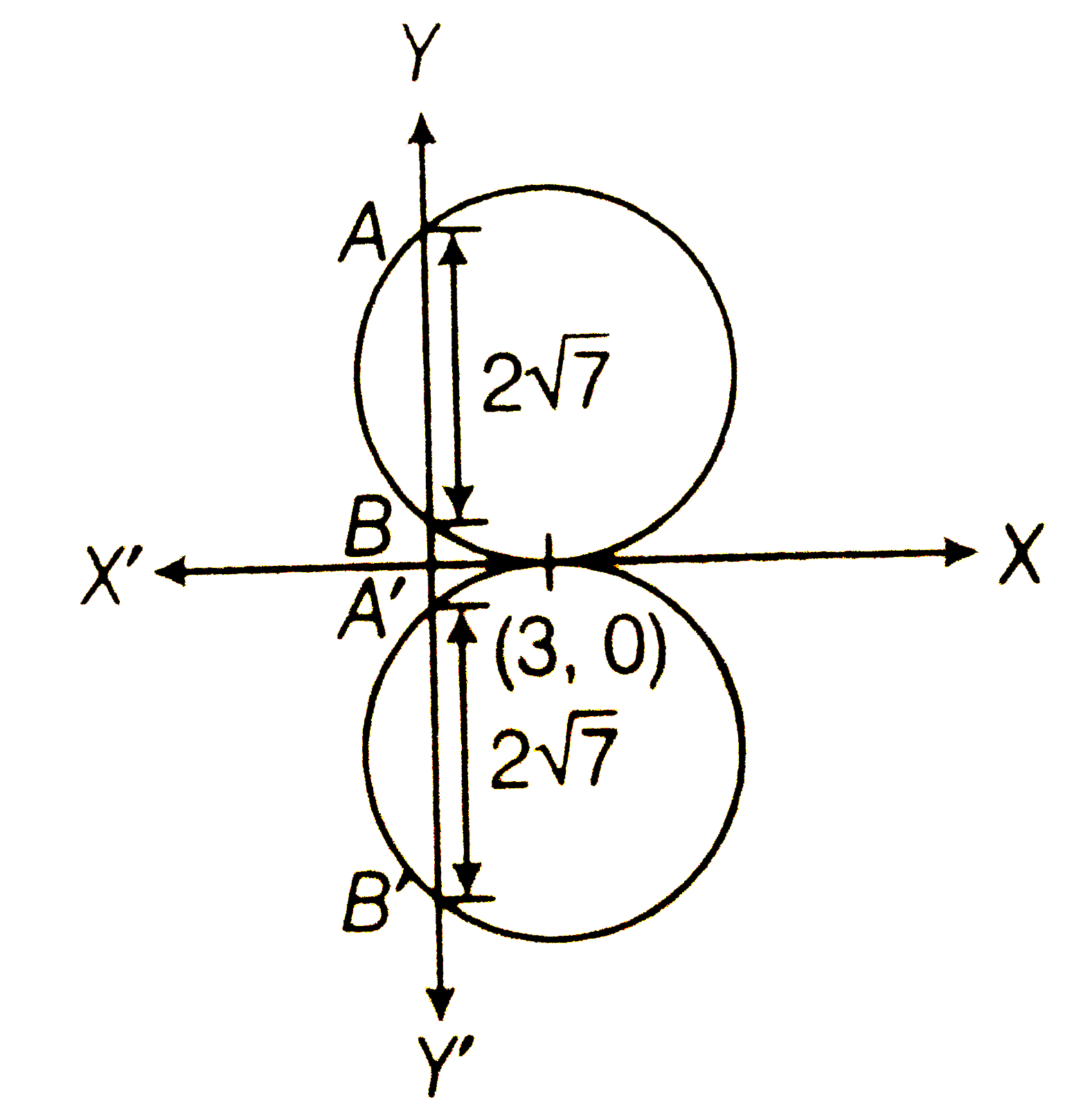
Topper's Solved these Questions
Similar Questions
Knowledge Check
Circle(s) touching x-axis at a distance 3 from the origin and having an intercept of length 2√7 on y-axis is (are)
Ax2+y2−6x+8y+9=0Bx2+y2−6x+7y+9=0Cx2+y2−6x−8y+9=0Dx2+y2−6x−7y+9=0Find the equation of a circle which touches y−aξs at a distance of 4units from the origin and cutsan intercept of 6units along the positive direction of x−aξs.
Ax2+y2+10x−8y+10=0Bx2+y2±10x−8y+16=0Cx2+y2+10x±8y+16=0Dnone
Find the equation of the circle touching the negative y−axis at a distance 5 from the origin and intercepting a length 8 on the x-axis.
View SolutionFind the equation of the circle which touches the axis of y at a distance 4 from the origin and cuts off an intercept of length 6 on the axis of x.
View SolutionFind the equation of a circle which touches y-axis at a distance of 2 units from the origin and cuts an intercept of 3 units with the positive direction of x-axis
View SolutionFind the equation of the a circle which touches y-axis at a distance of 4 units from the origin and cuts an intercept of 6 units along the positive direction of x-axis.
View SolutionFind the equation to the circle which touches the axis of x at a distance+3 from the origin and intercepts a distance 6 on the axis of y
View SolutionFind the equation of a circle which touches y-axis at a distance of 4units from the origin and cuts an intercept of 6units along the positive direction of x-a xis
View Solution
